Министерство высшего и среднего специального образования РСФСР

Липецкий политехнический институт

Кафедра прикладной механики

Расчётно-графическая работа №1 по курсу «Прикладная механика»

Задания и некоторые методические указания

Составитель В.Я. Баранцов

Липецк 1990

620.10(07)

Б.243

Расчетно-графическая работа №1 по курсу «Прикладная механика»

Задания и некоторые метод. указ. 2-е изд, исправл. и дополн.

/ Липецкий политехнический институт; сост. В.Я. Баранцов. Липецк, 1990, 28 с.

Предназначена для студентов 2 курса немеханических и немашиностроительных специальностей.

Расчетно-графическая работа №1 состоит из одиннадцати задач, охватывающих наиболее важные разделы основ расчетов на прочность и жесткость, Приведенные методические указания и примеры решения задач помогут студентам в самостоятельной работе над заданием.

Табл.4. Ик.8

Рецензент В.И. Халеев

Основным критерием работоспособности деталей машин и механизмов, а также элементов конструкций и сооружений является прочность, поэтому именно расчеты на прочность позволяют установить их минимально необходимые размеры. При этом размеры детали или элемента конструкции должны быть такими, чтобы они удовлетворяли и другим основным критериям работоспособности, например жесткости.

С целью приобретения элементарных практических навыков по расчетам на прочность и жесткость программой курса “Прикладная механика” предусмотрено выполнение студентами расчетно-графического задания состоящего из ряда задач.

При выполнении задания необходимо учесть, что успешное решение каждой последующей задачи возможно только при условии правильного решения предыдущей.

Этап 1. Построение эпюр внутренних силовых факторов для различных случаев нагружения брусьев.

Задача 1. Брус нагружен осевыми силами (рис.1). Исходные данные приведены в табл.1. Построить эпюру продольных сил.

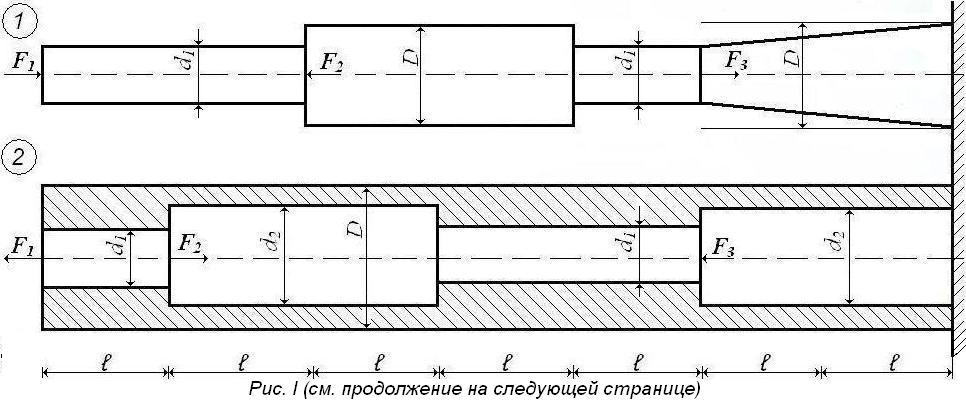
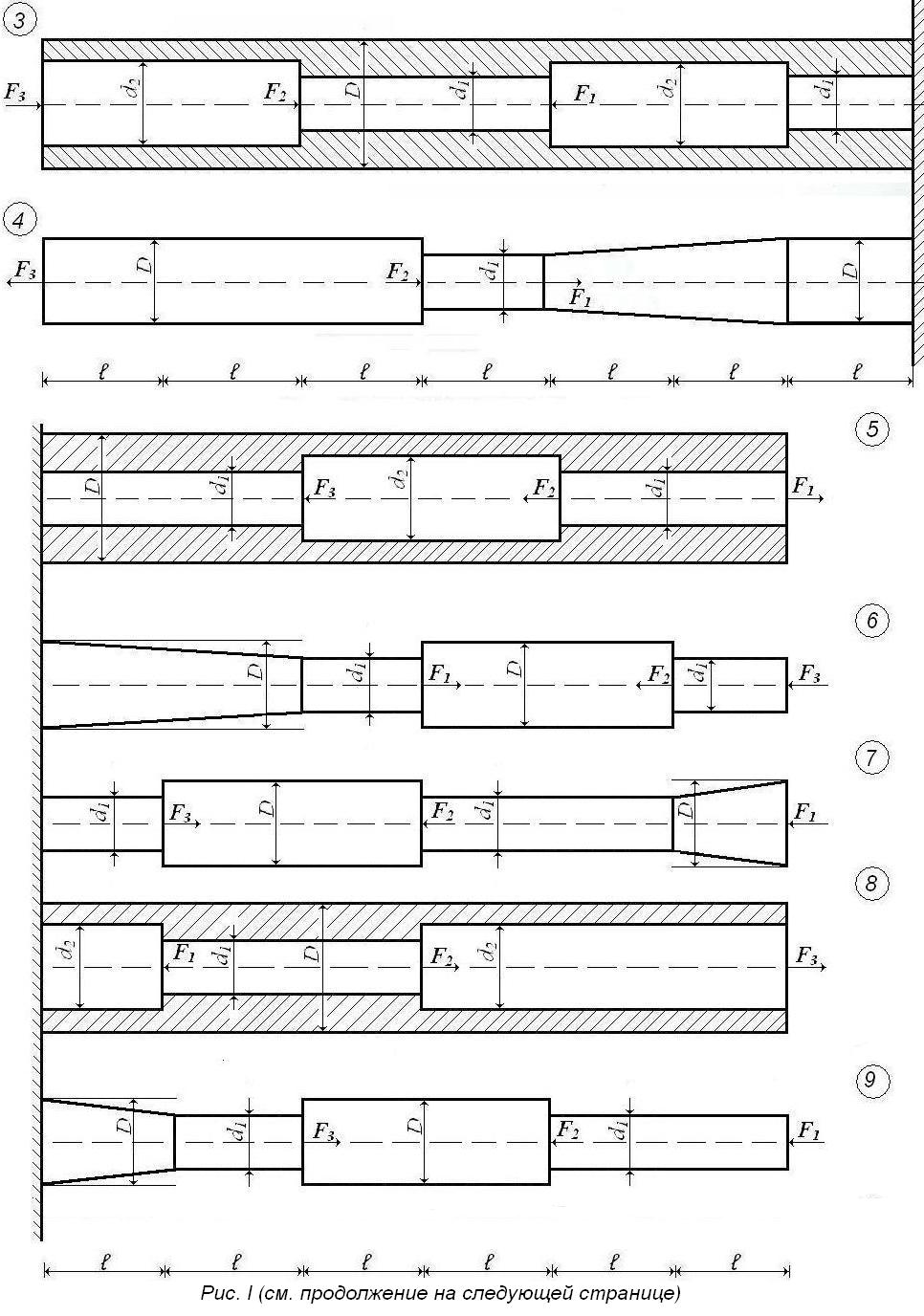
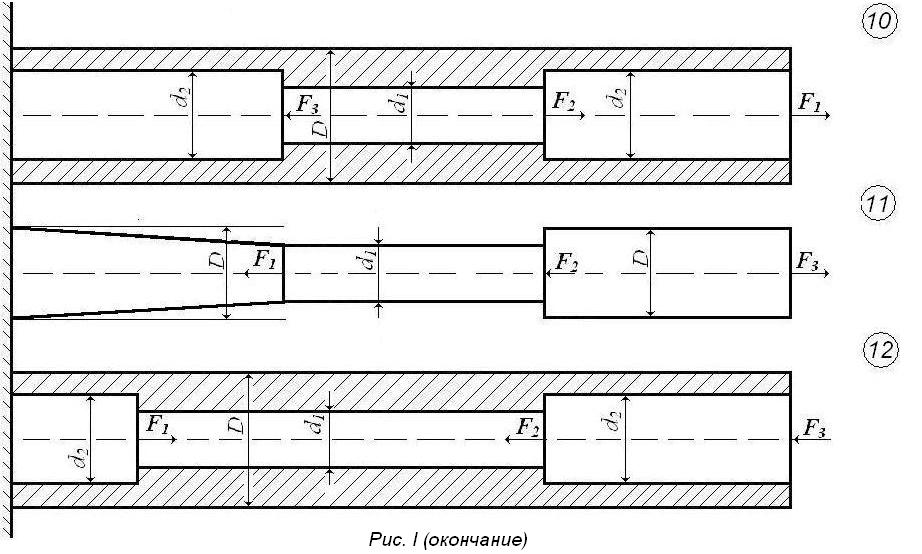
Таблица 1

Исходные данные к задаче 1

ВНИМАНИЕ! В этой и других таблицах знак «минус» у величин сил (моментов) означает, что необходимо изменить направление этих сил (моментов) на противоположное и считать их положительными.

Вариант	F1, кН	F2, кН	F3, кН	l, мм
1	200	400	300	100
2	-800	500	400	150
3	-400	800	200	200
4	300	300	200	150
5	-200	600	500	200
6	200	200	600	100
7	-100	500	600	200
8	-300	600	300	150
9	-200	600	400	180
10	-300	300	200	200
11	100	400	600	100
12	200	400	400	120
13	100	300	500	150
14	200	300	600	100
15	-100	400	200	200
16	-100	600	500	180
17	-300	400	300	200
18	-200	500	400	150
19	-200	100	300	100
20	-100	300	200	120
21	400	100	600	80
22	300	100	600	100
23	200	300	500	100
24	-300	300	300	200
25	300	300	500	80

Задача 2. Вал нагружен вращающими моментами (рис. 2). Значения моментов и длины участков вала даны в табл. 2. Построить эпюру крутящих моментов Т.

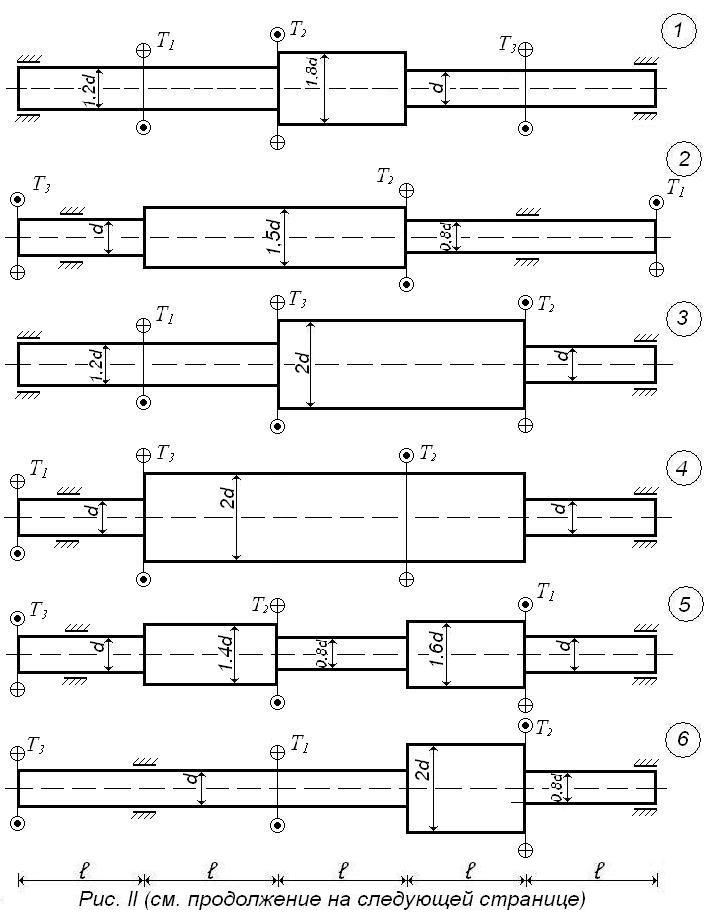
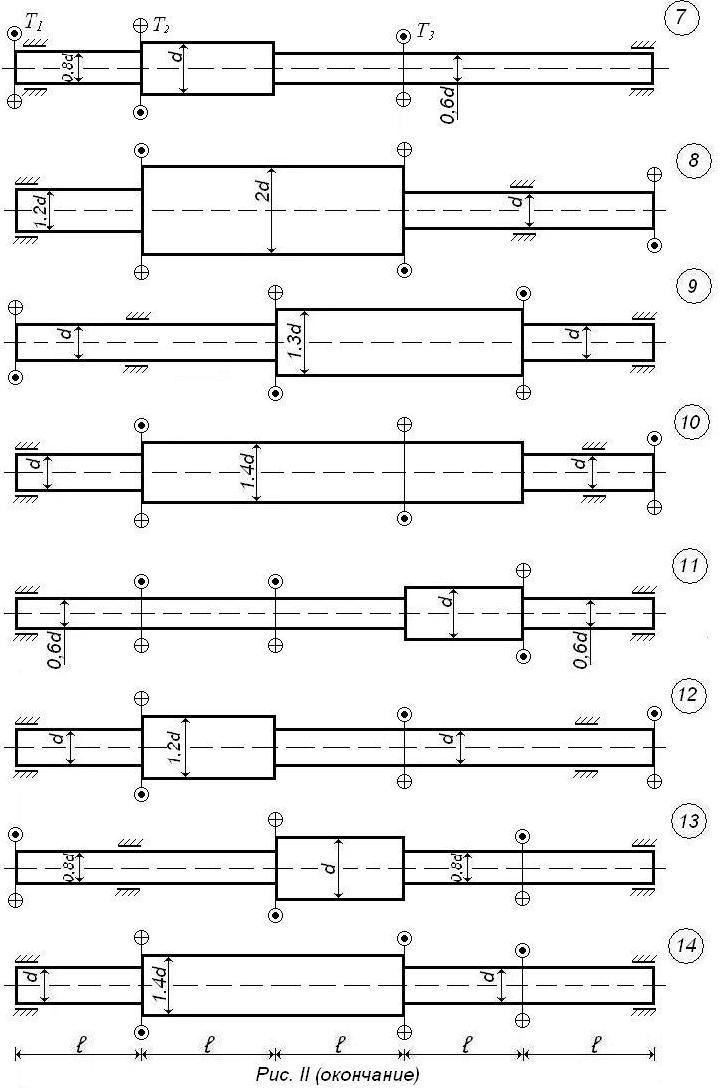
Таблица 2

Исходные данные к задаче 2

Вариант	Т1, кН*м	Т2, кН*м	Т3, кН*м	l, мм
1	0,5	1,2	0,7	100
2	0,6	1,0	0,4	85
3	0,5	0,9	0,4	70
4	0,3	0,8	0,5	100
5	0,4	0,8	0,4	90
6	-0,5	0,1	0,6	80
7	-0,4	-0,1	0,3	75
8	-0,5	-0,2	0,3	85
9	-0,3	0,2	0,5	95
10	-0,1	0,3	0,4	100
11	0,7	0,2	-0,5	90
12	0,6	0,3	-0,3	80
13	0,7	0,4	-0,3	100
14	0,6	0,1	-0,5	100
15	0,4	0,3	-0,1	95
16	0,8	0,3	-0,5	85
17	0,7	1,2	0,5	75
18	0,8	1,6	0,8	90
19	0,6	1,4	0,8	80
20	0,3	1,0	0,7	70
21	0,7	0,3	-0,4	75
22	0,6	0,5	-0,1	80
23	0,3	0,9	0,6	90
24	0,6	1,1	0,5	95

Задача 3. Построить эпюры поперечных сил и изгибающих моментов для балки на двух опорах (рис. 3, табл. 3).

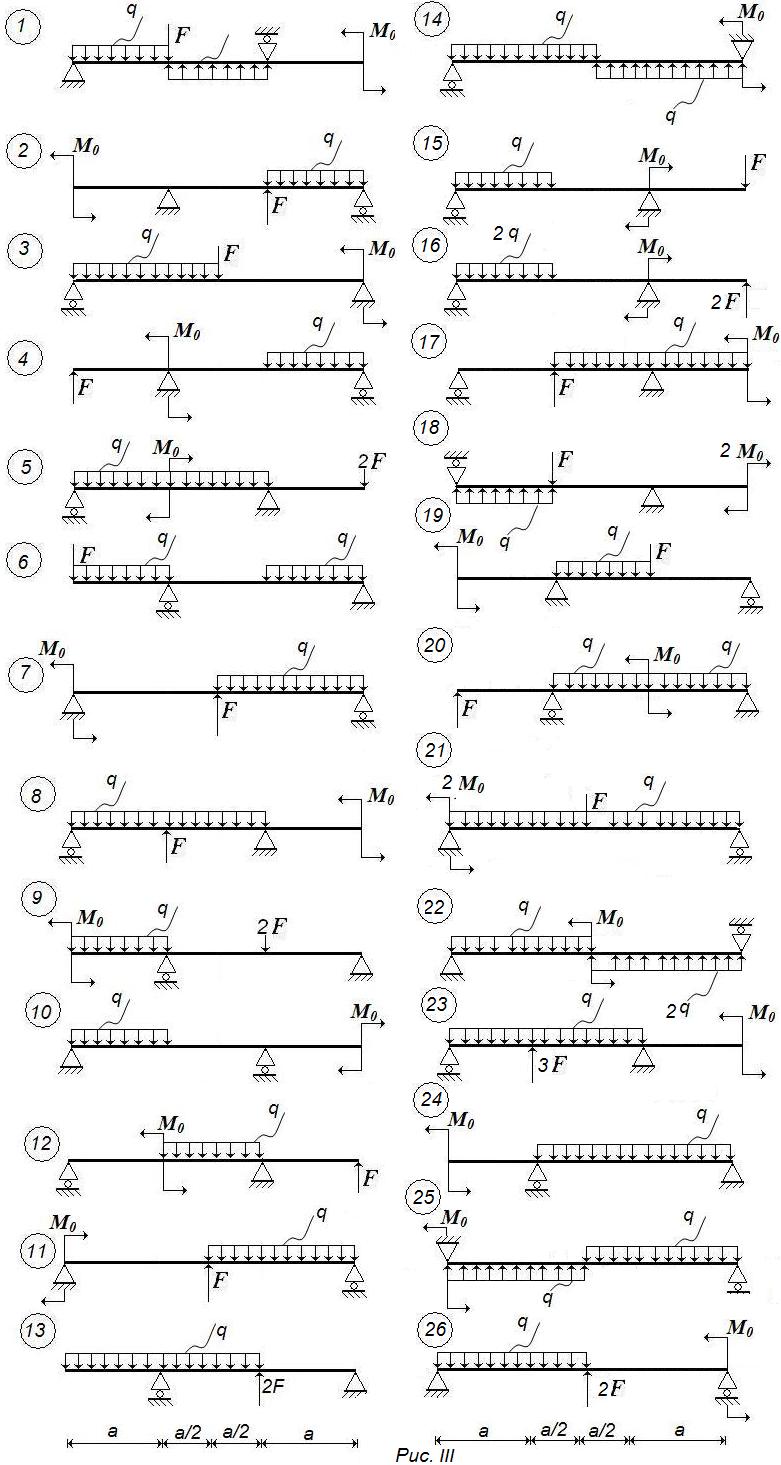
Таблица 3

Исходные данные к задаче 3

Вариант	q, кН/м	F, кН	M0, кН*м	a, м
1	20	30	80	2
2	10	30	60	2
3	20	40	80	1
4	-20	50	40	1
5	10	-30	50	2
6	20	40	-60	2
7	-20	50	60	1
8	-10	40	60	2
9	-20	-60	80	1
10	20	40	-50	2
11	-20	-40	-60	2
12	10	50	60	2
13	20	80	-50	1
14	20	-60	80	1
15	20	30	40	2
16	-20	50	80	2
17	10	-60	60	2
18	-10	40	-40	2
19	-20	60	80	1
20	20	60	-80	2
21	20	-30	60	2
22	10	-30	-50	1
23	20	40	80	1
24	10	50	60	2
25	20	60	-60	1
26	20	30	-40	2

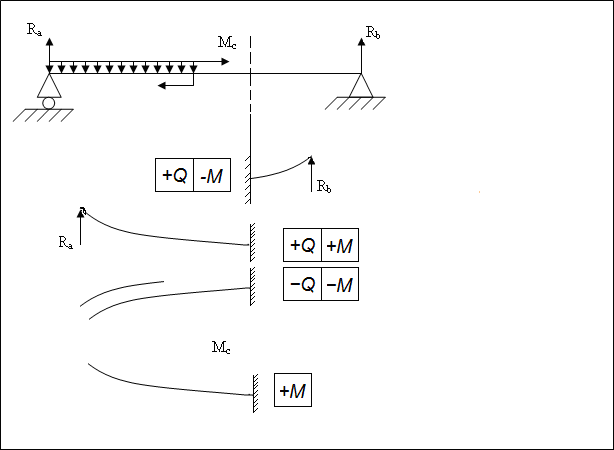
Задача 4. Построить эпюры поперечных сил Q и изгибающих моментов М для консольной балки (рис. 4, табл. 4) Ординаты эпюр выразить через q. При этом F = K1qa; M0 = K2qa .

Таблица 4

Исходные данные к задаче 4

Вариант	K1	K2	a, м	№ двутавра
1	5,0	5	1,6	22
2	6,0	4	1,8	24
3	4,5	6	2,0	30a
4	3,0	10	1,2	27
5	2,0	12	1,4	30
6	1,5	15	1,5	36
7	2,5	10	1,5	55
8	3,0	6	1,7	22a
9	4,0	8	1,9	27a
10	5,5	10	1,9	30
11	1,5	7	1,3	33
12	2,5	8	1,6	36
13	2,0	7	1,8	40
14	3,5	3	1,0	30
15	3,0	5	1,2	36
16	1,0	10	1,4	40
17	5,0	6	1,5	50
18	4,0	12	1,5	20a
19	3,5	9	1,7	22
20	4,5	10	1,9	24a
21	3,0	7	2,0	27
22	2,5	12	1,3	33
23	2,0	4	1,6	40
24	4	14	1,2	36
25	5	15	1,0	33
26	5,5	14	1,8	27a

Этап 2. Расчеты на прочность

Задача 5. Для стального бруса, приведенного на рис.1 , по результатам построения эпюры N определить из условия прочности; размеры поперечных сечений при [δ] = 160 МПа и принять ближайшие стандартные по ГОСТ 6636-69 или СТ СЭВ 514-77. Построить эпюры распределения нормальных напряжений в опасном сечении и по длине стержня d2/D = 0,8; d1/D = 0,6.

Задача 6. Для балки на двух опорах (рис.3) по результатам построения эпюры M подобрать стандартные размеры сечений стальной балки из условия прочности по нормальным напряжениям: двутаврового, прямоугольного с соотношением сторон h/b = 2, круглого диаметром d, кольцевого с соотношением диаметров d/D = 0,9. Для стали Ст3 принять [δ] = 160 МПа. По ГОСТ 6636-69 или СТ СЭВ 514-77 окончательно принять стандартные размеры сечений. Для каждого из четырех вариантов профиля балки построить эпюры распределения нормальных напряжений δ в опасном сечении. Определить коэффициенты выгодности сечений по отношению к двутавру:

k1 = AПРЯМ /AДВУТ; k2 = AКРУГА /AДВУТ; k3 = AКОЛЬЦА /AДВУТ;

и сделать вывод рациональности практического использования для балок данных профилей.

Задача 7. Для консольной балки (рис.4) из условия прочности определить допускаемые значения нагрузки: [q], [F], [M0] приняв для стали Ст3 [δ] = 160 МПа.

Этап 3. Расчеты на жесткость

Задача 8. Для бруса, рассмотренного в задачах 1 и 5 определить абсолютное удлинение ∆l и построить эпюру перемещений по длине бруса. Для конусного участка жесткость сечения ЕА определить по среднему диаметру: Е = 2,15*10 МПа.

Задача 9. Для двутавровой балки на двух опорах, рассмотренной в задачах 3 и 6, определить прогиб в середине пролета (пролетом l называется расстояние между опорами) с помощью интеграла Мора или приема Верещагина. Сравнить полученное значение прогиба с допускаемым, [ƒ] = l/300.

Если полученное значение прогиба больше допускаемого, подобрать размер двутавра из условия жесткости.

Изобразить ось изогнутой балки, используя эпюру М.

Задача 10. Для консольной балки, рассмотренной в задачах 4 и 7, определить прогиб конца консоли с помощью интеграла Мора или приема Верещагина. Изобразить ось изогнутой балки, используя эпюру изгибающих моментов М.

Задача 11. Для сплошного стального вала, рассмотренного задаче 2, определить размеры поперечных сечений (диаметры) из условия прочности при [τ] = 20 МПа и принять стандартные значения по ГОСТ 6636-69 или СТ СЭВ 514-77. Построить эпюру распределения касательных напряжений в опасном сечении, эпюру распределения максимальных касательных напряжений по длине вала и эпюру углов закручивания по длине вала относительно левого торцевого сечения, приняв G = 0,8*10 МПа.

Методические указания к выполнению этапа 1

Для определения внутренних силовых факторов в поперечных сечениях стержней при различных видах нагружения необходимо для каждого участка применить метод сечений. При этом под длиной участка подразумевается расстояние между точками приложения сил или моментов (также между началом или концом приложения распределенной нагрузки).

Продольная сила в сечении равна сумме проекций на ось бруса всех внешних сил с одной стороны от сечения. При этом внешние силы, отрывающие рассматриваемую часть стержня от сечения, берутся со знаком «плюс» прижимающие – со знаком «минус» (необходимо помнить, что к внешним силам относятся опорные реакции).

Крутящий момент в сечении равен сумме всех вращающих моментов с одной стороны от сечения. Для получения знака крутящего момента необходимо вращающие моменты (внешние), направленные против хода часовой стрелки, если смотреть со стороны отброшенной части, записывать со знаком «плюс».

При плоском изгибе в поперечных сечениях балок в общем случае действуют два внутренних силовых фактора: поперечная сила и изгибающий момент.

Поперечная сила в сечении балки равна сумме проекций на сечение всех внешних сил (в том числе и реакций) с одной стороны от сечения. При этом внешние силы, вращающие рассматриваемую часть по часовой стрелки (если мысленно закрепить ее в сечении), записываются со знаком «плюс» (см. рис.5).

Изгибающий момент в сечении балки равен сумме моментов всех внешних сил (в том числе и опорных реакций) относительно сечения с одной стороны. Для получения знака изгибающего момента необходимо моменты внешних сил, в т. ч. и сосредоточенные моменты, изгибающие рассматриваемую часть выпуклостью вниз, записывать со знаком «плюс», как показано на рис. 5.

Внутренние силовые векторы в сечениях балок зависят от внешних нагрузок и изменяются по длине балки, поэтому их удобно представлять в виде эпюр, ординаты которых для любых сечений по длине балки дают соответствующие значения поперечной силы или изгибающего момента . При этом положительные значения откладываются вверх от оси эпюры, отрицательные — вниз; ось эпюры проводят параллельно оси балки. При этом для эпюры М положительные значения оказываются со стороны сжатых волокон и знак на поле эпюры М не ставят.

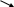
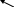
Пример 1

Построение эпюр поперечной силы и изгибающего момента для балки показанной на рис. 6, а.

1) Определяем опорные реакции. Считаем, что обе реакции направлены вверх.

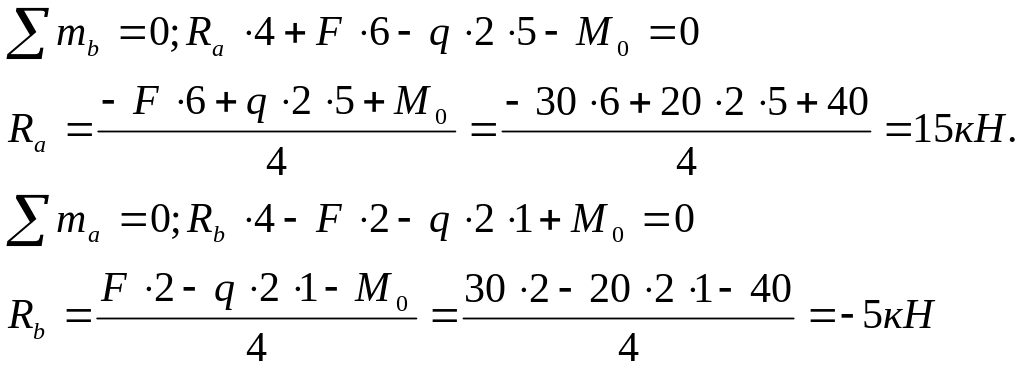
Знак (-) означает, что направлена противоположно.

Меняем направление реакции и считаем ее положительной.

Проверка:

т.е. реакции определены верно.

2) Определяем Q и M на участках балки.

1 участок: 0 ≤ z ≤ 2 м

Q = F - qz; QZ=0 = F = 30 кН; QZ=2 =30 – 20*2 = -10 кН.

M = F*z – qz /2; MZ=0 = 0; M Z=2 = 30*2 - 20*2 /2 = 20 кН*м.

2 участок: 0 ≤ z ≤ 2 м

Q = = 5 кН;

M = - * z;

MZ=0 = 0; M Z=2 = -5*2 = -10 кн*м

3 участок: 0 ≤ z ≤ 2 м

Q = = 5 кН; M = - *(z+2) + M0;

MZ=0 = -5*2 + 40 = 30 кН*м; M Z=2 = -5(2+2) +40 = 20 кН*м

Выбираем масштаб и строим эпюру (рис. 5,б).

Как видно из рис. 5,б, на участке 1 эпюра Q меняет знак, что указывает на наличие экстремальной точки на эпюре M в этом сечении.

Определяем значение z0, для чего приравниваем выражение для Q на 1 участке к нулю

Q = F - q z0 = 0;

30 - 20z0 = 0; z0 = 30/20 = 1,5 м.

Подставляем значение z0 в выражение для M на 1 участке:

Mmax = 30*1,5 – 20*1,5 /2 = 22,5 кН*м.

Выбираем масштаб и строим эпюру М (рис. 5,в).

Из-за простоты указания к этапу 2 не приводятся.

Методические указания к выполнению этапа 3.

обычно задача 8 выполняется студентами без особых затруднений, поэтому уделим внимание только задачам 9... 11.

Для определения перемещений при изгибе с помощью интеграла Мора необходимо на вспомогательной системе в сечении, для которого нужно определить прогиб (угол поворота сечения), приложить единичную безразмерную силу (единичный безразмерный момент) и записать для каждого из участков выражение для изгибающего момента m, от действия единичной силы (единичного изгибающего момента). При EJk = const по длине балки искомое перемещение равно

при определении прогиба

θ

при определении угла поворота сечения, где Mi - выражение для момента от внешних нагрузок для основной системы на данном участке;

- выражение для момента от единичной безразмерной силы для вспомогательной системы на том же участке;

- выражение для момента от единичного безразмерного момента для вспомогательной системы на том же участке. При этом нужно помнить, что текущая абсцисса z на основной и вспомогательной системах для каждого участка должна быть обозначена одинаково и должна изменяться а тех же пределах.

Пример 2

Определение прогиба конца консоли (точка К) для двутавровой (№ 20) балки изображенной на рис. 6,а.

Ба вспомогательной системе прикладываем единичную безразмерную силу в точке К, где нужно определить прогиб, и определяем опорные реакции (рис. 6,г). Для каждого из участков записываем выражения М и

1 участок: 0 ≤ z ≤ 2 м ; M = F*z – qz /2; m1 = -z;

2 участок: 0 ≤ z ≤ 2 м ; M = Rb*z; m1 = - z

3 участок: 0 ≤ z ≤ 2 м ; M= -Rb(2+z) + M0; m1 = - (2+z)

Записываем сумму интегралов Мора по длине каждого участка

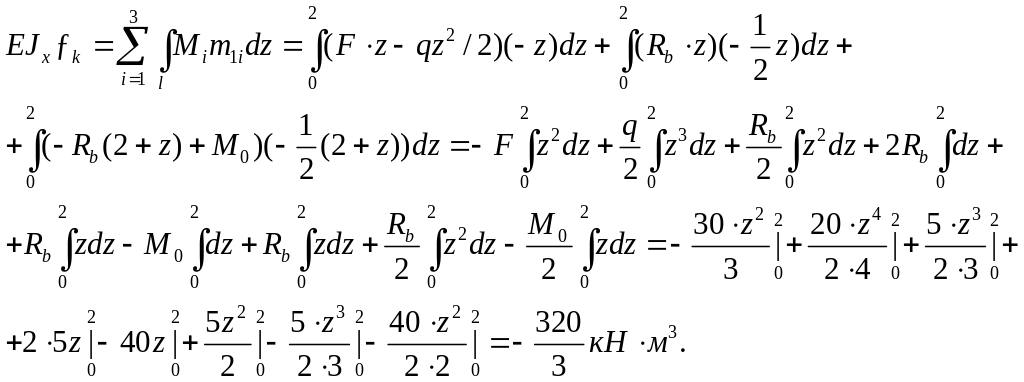
Искомый прогиб балки в точке К

Полученный знак минус указывает на то, что направление прогиба противоположно направлению единичной силы т.е, точка К перемещается вверх.

Для вычисления интегралов Мора с помощью приема Верещагина необходимо построить эпюру изгибающих моментов от единичной безразмерной силы (единичного безразмерного момента) приложенной в сечении, где определяется прогиб (угол поворота сечения) и «перемножить» эпюру изгибающих моментов («грузовую») на единичную. При этом

ω ,

где ω - площадь эпюры М на данном участке;

- значение ординаты на единичной эпюре под центром тяжести «грузовой» эпюры на данном участке.

Если определение положения центра тяжести участка эпюры затруднено, можно воспользоваться «правилом дирижера»:

ω

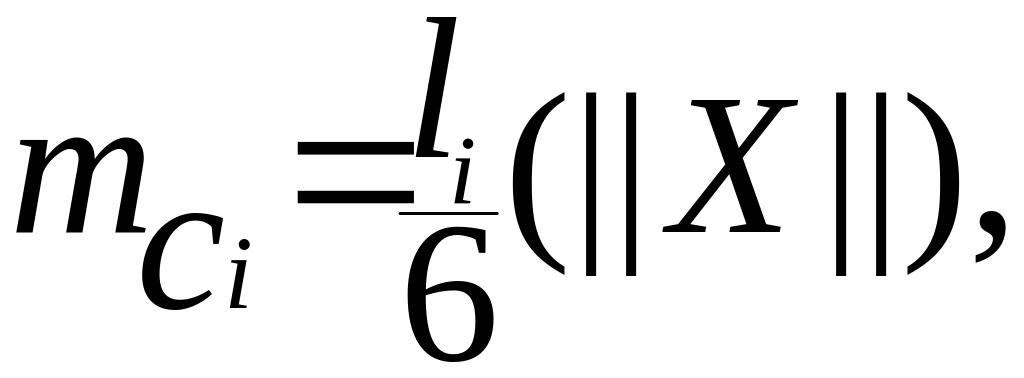
где - длина данного участка.

Например, на каком-то участке эпюры М и m имеют вид, как показано на рис. 7.

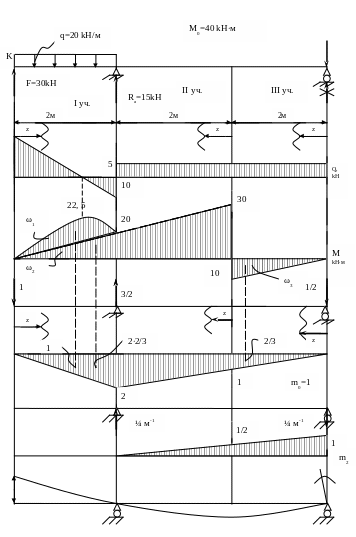
Рис. 6

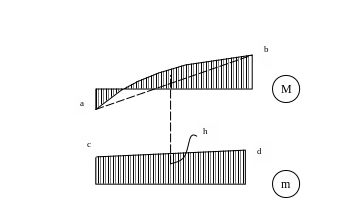
Рис. 7

Здесь /12 - площадь «чистой» параболы (q – интенсивность распределенной нагрузки на данном участке балки, l – длина данного участка);h - значение ординаты под центром тяжести «чистой» параболы.