Система дифференциальных уравнений движения бла

;

;

;

;

;

(4.17)

должна быть дополнена уравнениями связей, обеспечивающих выработку и формирование управляющих воздействий по каждой физической оси БЛА.

4.6. Математическая модель системы управления движением бла

Из анализа системы дифференциальных уравнений (4.17) вытекает перечень задач, которые необходимо решать на борту в полете БЛА:

• задача наведения, решение, которой, позволяет обеспечить выполнение боевой задачи с требуемой эффективностью;

• задача стабилизации, решение, которой, обеспечит удержание параметров движения БЛА, определяемых задачей наведения, вблизи программных значений.

В свою очередь задача стабилизации делится на частные задачи.

Исходя из анализа уравнений линейного движения центра масс БЛА обуславливается:

• необходимость стабилизации продольной скорости ракеты; эту задачу должна решать система регулирования кажущейся скорости (РКС);

• необходимость стабилизации движения корпуса ракеты в плоскости стрельбы; эту задачу должна решать система боковой стабилизации (БС);

• необходимость стабилизации движения корпуса ракеты в плоскости местного горизонта; эту задачу должна решать система нормальной стабилизации (НС).

Решения уравнения связей, обуславливающие выработку управляющих сил и моментов в каждый момент времени, должны определяться с учетом действия на БЛА реальных возмущений.

Произведем линеаризацию системы уравнений (4.17), учитывая следующие допущения:

- угловые скорости движения корпуса БЛА относительно гироскопической инерциальной системы координат при нормальной работе системы угловой стабилизации близки к нулю;

, т.е. величина продольной скорости БЛА является преобладающей;

– величины второго порядка малости.

В результате принятых допущений дифференциальные уравнения движения БЛА примут следующий вид:

;

;

;

;

;

. (4.18)

Преобразуем систему дифференциальных уравнений (4.18) к векторно-матричному виду, наиболее удобному для решения уравнений бортовым цифровым вычислительным комплексом системы управления БЛА.

Для упрощения изложения и восприятия материала рассмотрим методику преобразования на примере преобразования уравнений углового движения БЛА.

Для общности подхода введем в уравнения углового движения демпфирующие моменты, имеющие место при движении БЛА на атмосферном участке траектории. Тогда уравнения примут вид:

;

;

, (4.19)

где  - коэффициент динамической вязкости среды движения БЛА.

Введем новые переменные и преобразуем дифференциальные уравнения (1) к стандартному виду Коши:

;

;

. (4.20)

КОШИ (Cauchy) Огюстен Луи (1789-1857), французский математик, иностранный почетный член Петербургской АН (1831). Один из основоположников теории аналитических функций. Труды по теории дифференциальных уравнений, математической физике, теории чисел, геометрии. Автор классических курсов математического анализа.

Представим уравнения (10) в векторно-матричном виде:

; (4.21)

; ;

; ; ; .

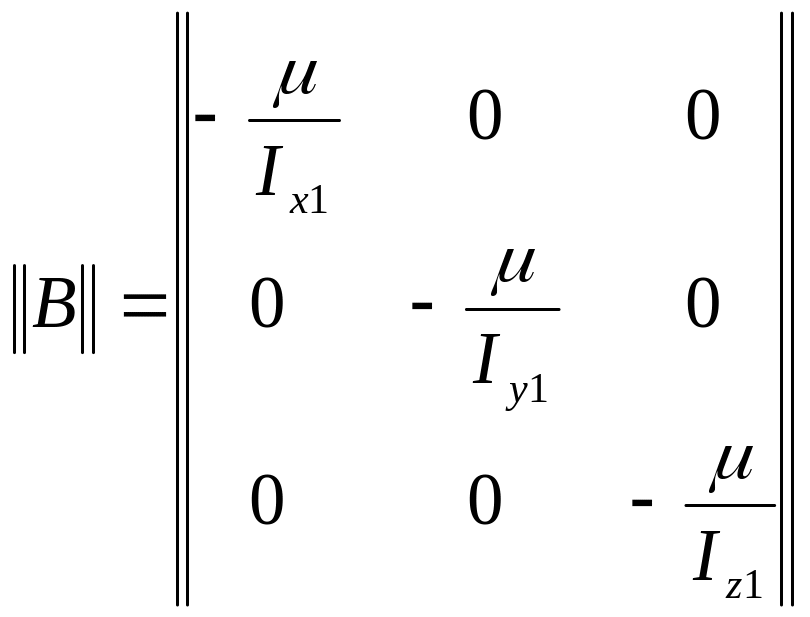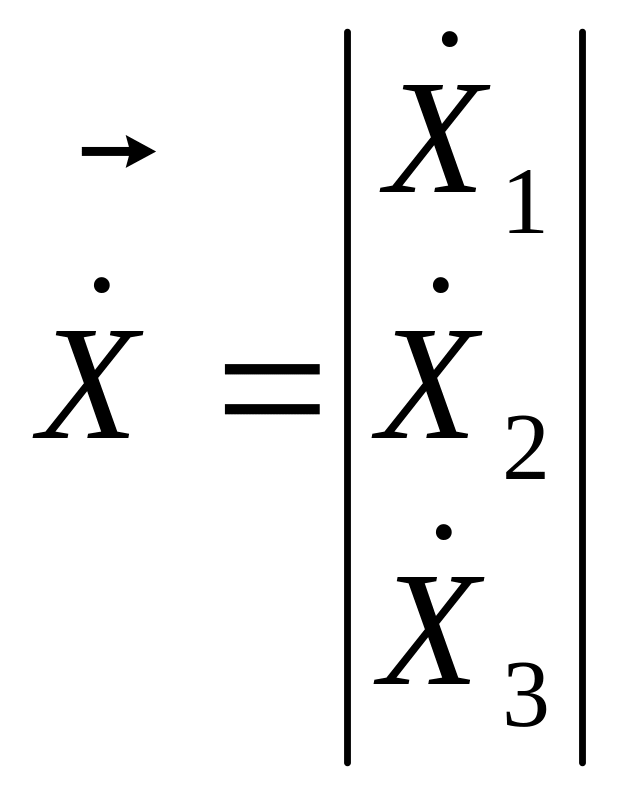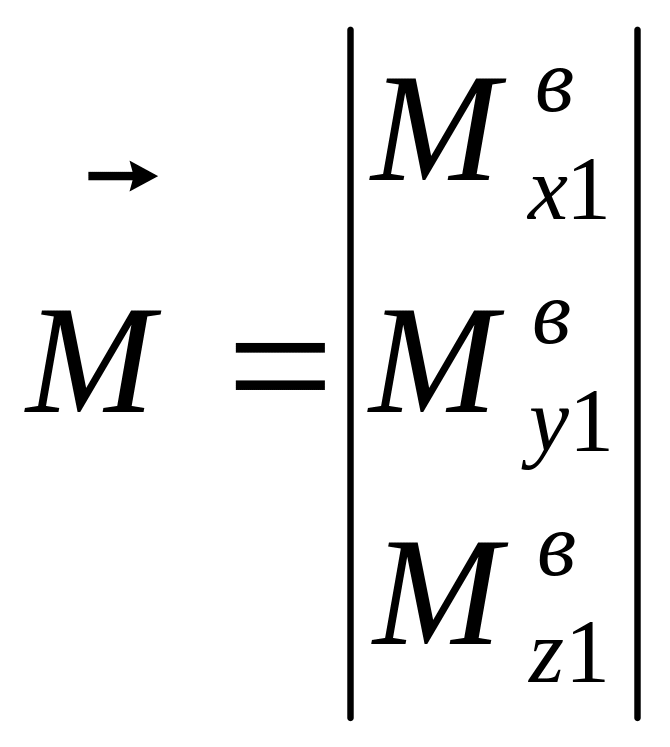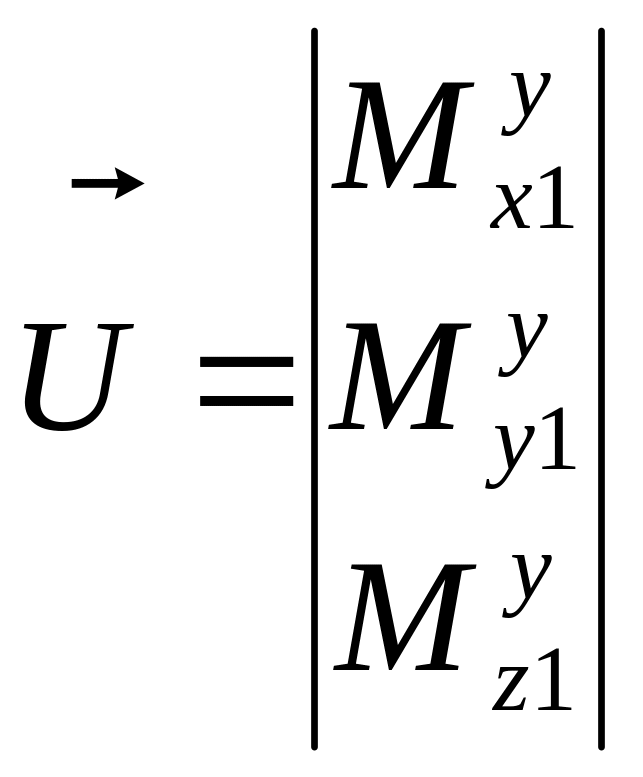Дополнительно введем матрицу связи – матрицу интегрирования, отражающую свойство любой механической системы интегрировать входные воздействия

. (4.22)

Матрица вместе с матрицей характеризует динамические свойства объекта регулирования - корпуса БЛА; матрица - восприимчивость БЛА к управляющим воздействиям; матрица - восприимчивость БЛА к возмущающим воздействиям.

Введем также матричное уравнение преобразователя физических параметров движения БЛА в электрические сигналы и матрицу – матрицу идеальных измерителей - матрицу информационно-измерительных устройств:

; . (4.23)

В результате решения задачи синтеза оптимального регулятора системы управления - одного из каналов бортовой цифровой вычислительной машины по какому-нибудь критерию (например, по критерию требуемого быстродействия) определяются коэффициенты матрицы БЦВК:

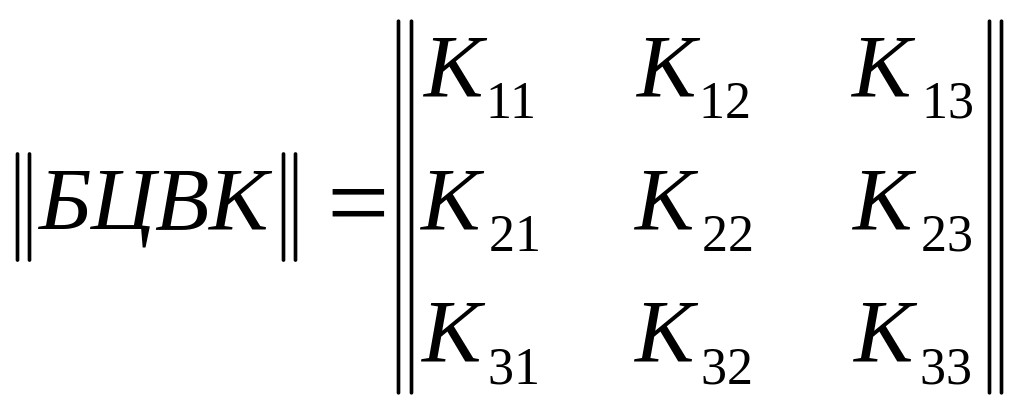. (4.24)

Требуемое управление, прикладываемое к БЛА в определенный момент времени, в общем случае определяется выражением:

. (4.25)

По векторно-матричному уравнению (4.21) с учетом выражений (4.22) – (4.25) построим структурно-матричную схему бортовой системы управления БЛА (рис. 4.7)

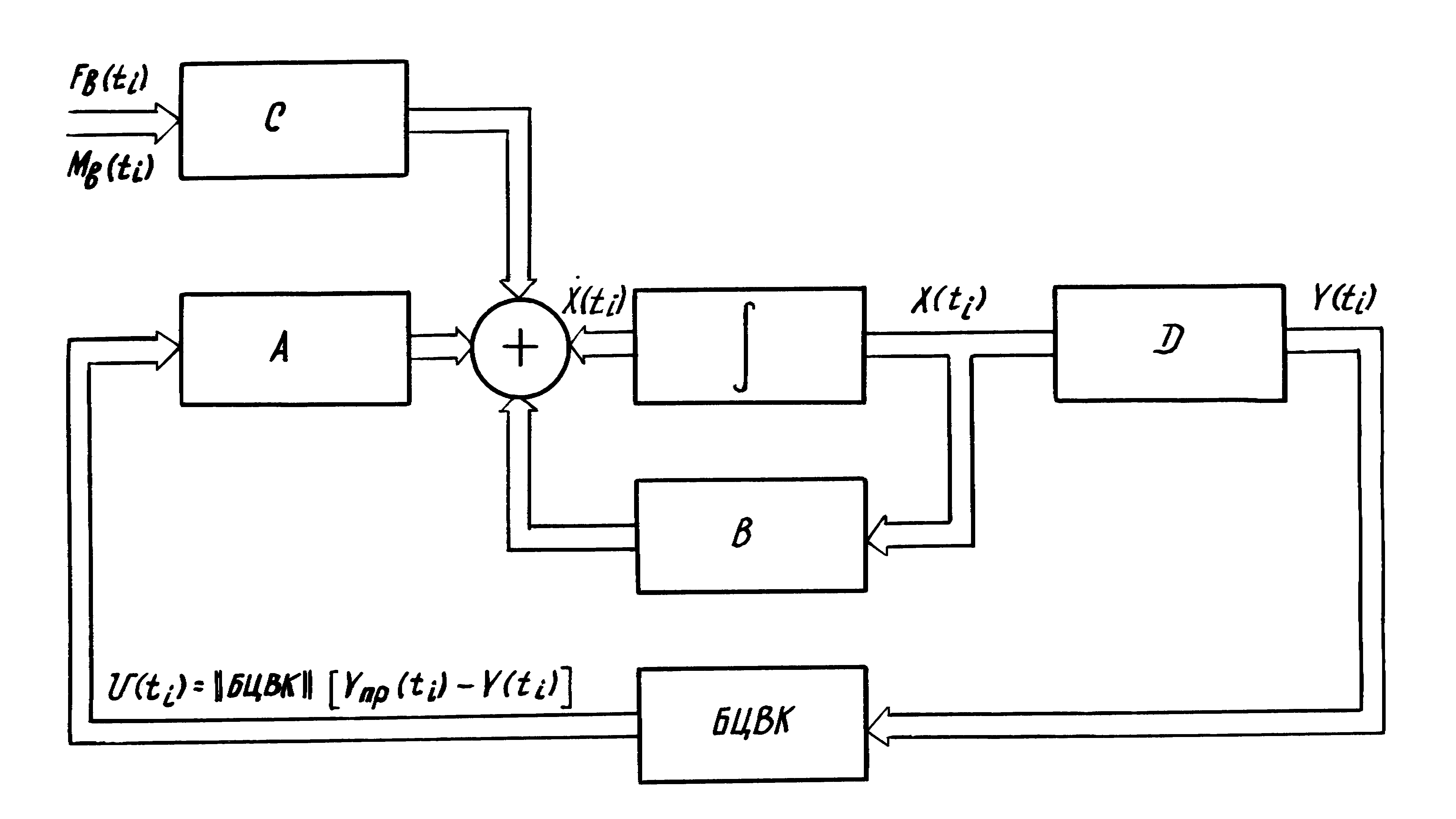
Рис.4.7. Структурно-матричная схема бортовой системы управления БЛА

Методика математического моделирования движения сложного динамического объекта - БЛА может быть сведена к перечню необходимых последовательных действий:

1. Составление уравнений поступательного движения центра масс БЛА.

2. Составление уравнений углового движения БЛА относительно центра масс.

3. Составление уравнений связей, обеспечивающих выработку и формирование управляющих воздействий по каждой физической оси БЛА.

4. Проведение (при необходимости) линеаризации математической модели.

5. Моделирование движения БЛА по расчетной траектории на универсальной или специализированной ЦВМ с целью оптимизации целого перечня параметров: геометрических, массовых, энергетических характеристик; оптимизации алгоритмов систем наведения и стабилизации и др.

6. Введение в математическую модель движения статистических данных, обуславливающих с большой степенью вероятности в полете по указанной траектории влияние определенных возмущающих факторов на динамику движения БЛА.

По результатам моделирования разрабатывается техническое задание на разработку эскизного проекта БЛА.