4.5. Уравнения углового движения бла

Допустим теперь, что OXYZ - инерциальная система координат (рис. 4.6). К системе постоянного состава, применима теорема классической динамики об изменении кинетического момента, которая формулируется так: производная по времени от кинетического момента системы относительно какого-либо неподвижного центра (в данном случае, относительно центра масс БЛА) равна сумме моментов всех внешних сил, действующих на систему относительно того же центра.

На основании изложенного, в фиксированный момент времени t

, (4.11)

где - соответственно главный момент всех внешних сил, действующих в момент времени t на БЛА.

Получим уравнения движения БЛА относительно центра масс, используя принцип затвердевания. Главный момент количества движения (кинетический момент) относительно центра масс твердого тела вычисляется по формуле

, (4.12)

где  - абсолютная угловая скорость БЛА, I – тензор инерции, т.е. матрица моментов инерции, имеющая следующий вид:

,

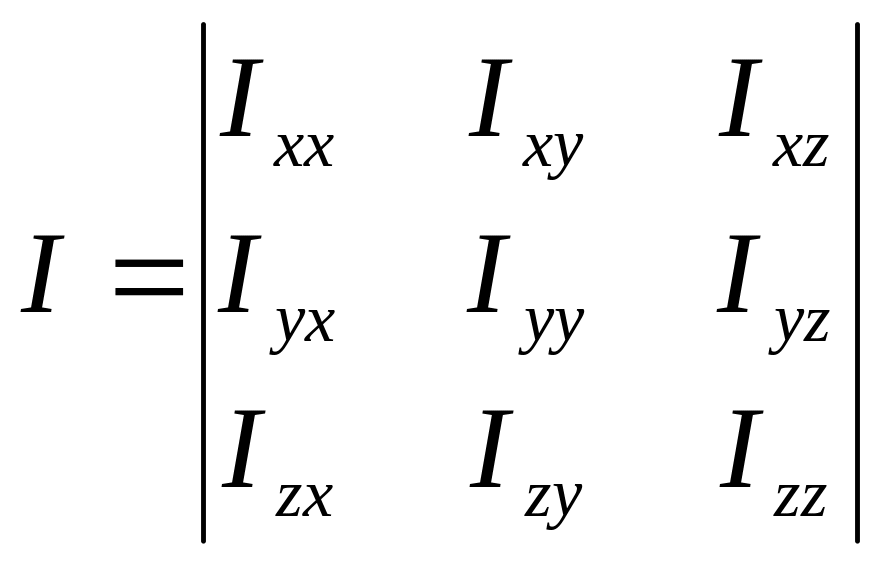где - осевые моменты инерции БЛА относительно связанных осей; - центробежные моменты инерции, причем для тел вращения , , .

В случае динамически симметричного корпуса БЛА, для которого оси связанной системы координат являются главными осями инерции и, следовательно, центробежные моменты инерции равны нулю. Тензор инерции в этом случае преобразуется к виду

.

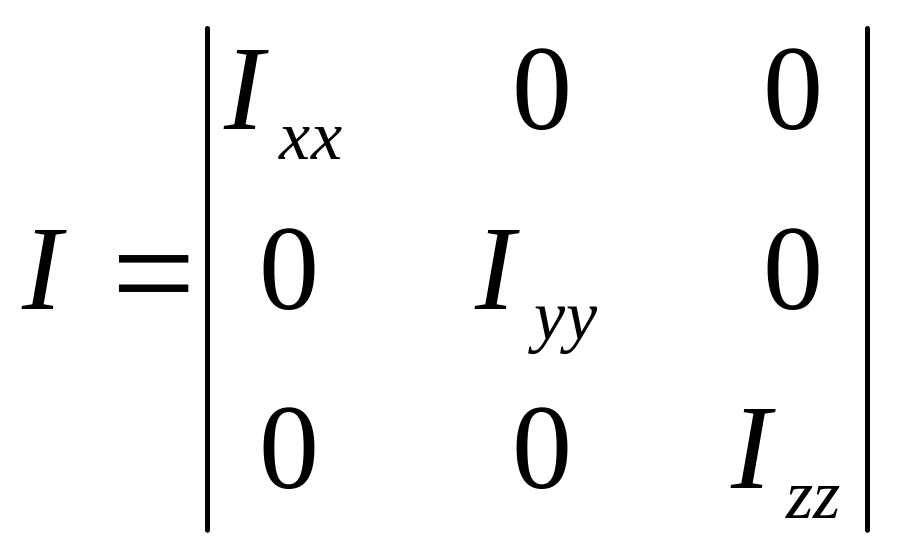Установим связь между производными по времени вектора в не вращающейся стартовой системе и вращающейся связанной системах координат:

, (4.13)

где - производная кинетического момента в связанной с корпусом БЛА системе координат, - главный момент всех внешних сил, тяги двигателя и кориолисовых сил.

С учетом выражения (4.12) и принятого допущения о постоянстве массы и формы корпуса БЛА (принцип затвердевания), получим

. (4.14)

Подставляя (4.12) и (4.14) в выражение (4.13) получим векторное динамическое уравнение Эйлера в связанной системе координат при допущении, что связанные оси являются главными осями инерции БЛА

. (4.15)

Для большинства БЛА это допущение справедливо, т.к. они конструктивно выполняются в виде тел вращения с равномерным распределением масс по объему.

Используя известное правило вычисления векторного произведения, определим

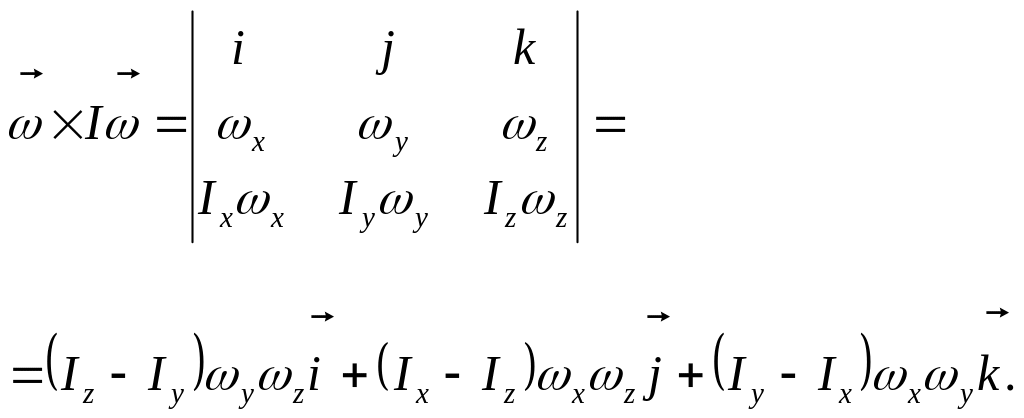
В соответствии с изложенным, уравнения углового движения бла в проекциях на связанные оси запишутся в виде:

;

; (4.16)

,

где , , - моменты инерции БЛА - относительно соответствующих связанных осей; , - угловые скорости движения корпуса БЛА относительно гироскопической инерциальной системы координат; , , - суммы прекций моментов возмущающих и управляющих сил на связанные оси.

ЭЙЛЕР (Euler) Леонард (1707-83), математик, механик, физик и астроном. По происхождению швейцарец. В 1726 году был приглашен в Петербургскую академию наук и переехал в 1727 году в Россию. Был адъюнктом (1726), а в 1731-41гг. и с 1766 г. академиком Петербургской академии наук (в 1742-66 г. иностранный почетный член). В 1741-66гг. работал в Берлине, член Берлинской академии наук. Эйлер - ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки.

Параметрами углового движения БЛА являются угловые скорости движения корпуса относительно его центра масс и углы тангажа - , рысканья -  и вращения (крена) - .

Измерителями параметров углового движения являются гироскопические приборы различных типов.