4.4. Уравнения поступательного движения центра масс бла.

Движение центра масс БЛА в связанной системе координат может быть записано согласно второму закону И.Ньютона векторным уравнением:

, (4.7)

где M - масса БЛА;

dV/dt - вектор абсолютного ускорения движения БЛА;

P -вектор силы тяги двигательной установки;

R- вектор полной аэродинамической силы;

G - вектор силы земного притяжения.

НЬЮТОН (Newton) Исаак (1643-1727), английский математик, механик, астроном и физик, создатель классической механики, член (1672) и президент (с 1703) Лондонского королевского общества. Фундаментальные труды «Математические начала натуральной философии» (1687) и «Оптика» (1704). Разработал (независимо от Лейбница) дифференциальное и интегральное исчисления. Открыл дисперсию света, хроматическую аберрацию, исследовал интерференцию и дифракцию, развивал корпускулярную теорию света, высказал гипотезу, сочетавшую корпускулярные и волновые представления. Построил зеркальный телескоп. Сформулировал основные законы классической механики. Открыл закон всемирного тяготения, дал теорию движения небесных тел, создав основы небесной механики.

Величина N = P + R называется поверхностной силой. С учетом этого обозначения, после деления обеих частей уравнения (4.7) на массу БЛА уравнение линейного движения БЛА приобретет вид

, (4.8)

где dW/dt - кажущееся ускорение - ускорение, сообщаемое БЛА силами негравитационного происхождения; g - ускорение силы тяжести.

Д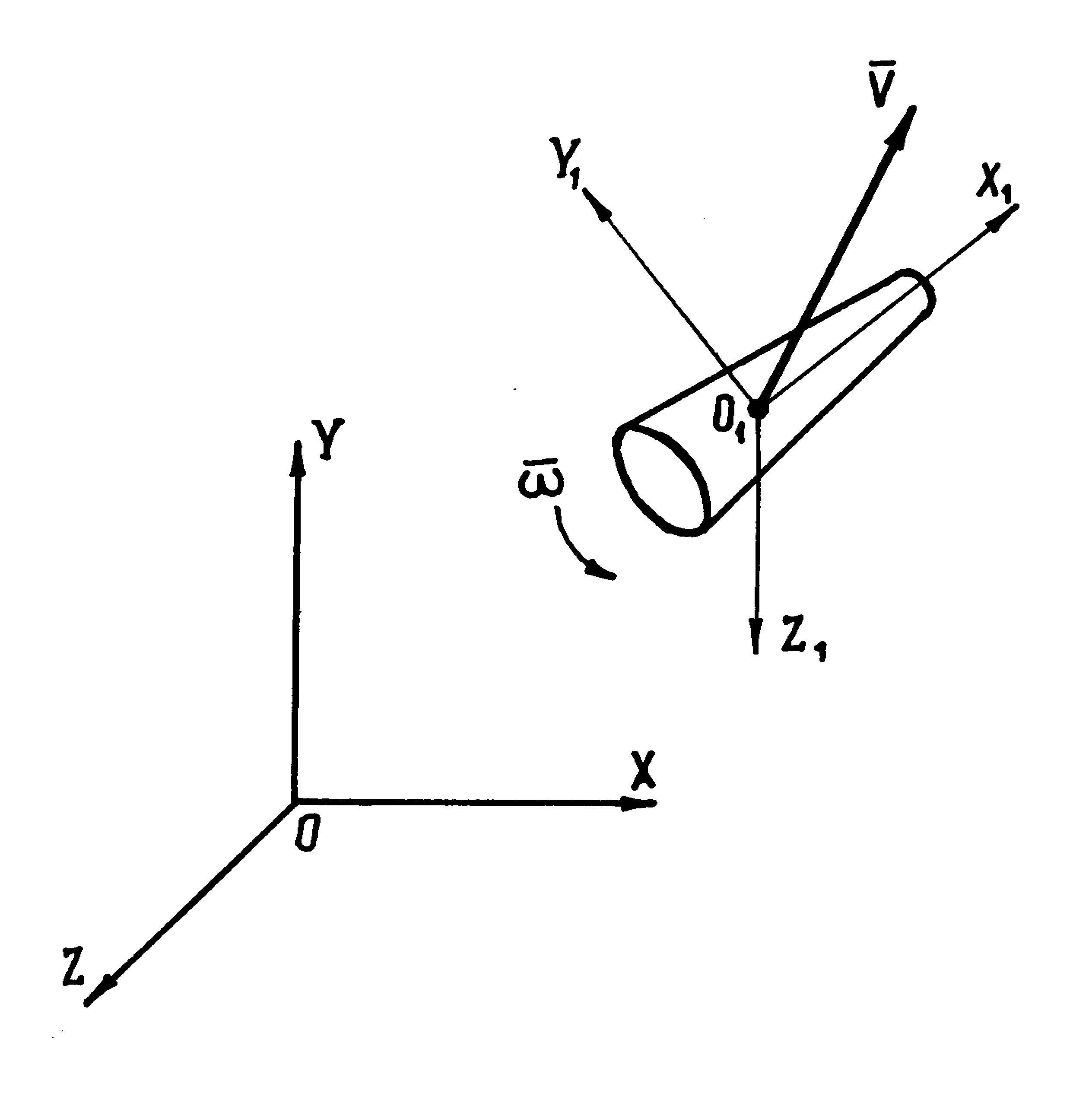 ля решения практических задач векторное уравнение часто заменяют эквивалентной системой скалярных уравнений, проецируя вектор параметров состояния системы на оси прямоугольной системы координат.

Рис. 4.6. Относительное движение БЛА

Спроецируем вектор абсолютной скорости движения БЛА dV/dt на оси связанной системы координат; учтем также, что корпус БЛА в общем случае совершает угловое движение относительно инерциальной системы координат с угловой скоростью  (рис.4.6).

Если есть производная вектора V относительно системы координат OXYZ , - производная этого же вектора относительно связанной системы координат и  - угловая скорость вращения связанной системы относительно неподвижной системы координат OXYZ, то

.

По известному правилу вычисления векторного произведения

.

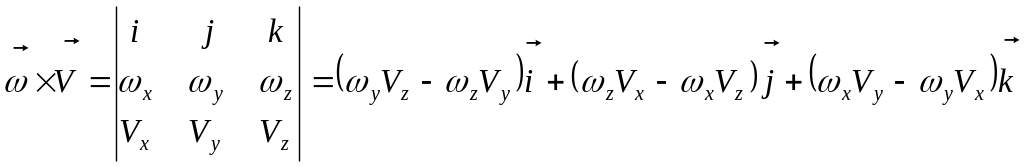В соответствии с изложенным, скорость относительного движения бла в проекциях на связанные оси

;

; (4.9)

.

С учетом выражения (4.9) векторное уравнение (4.7) можно представить тремя скалярными уравнениями

;

; (4.10)

,

где , , - проекции вектора кажущегося ускорения центра масс на оси связанной системы координат;

, , - проекции возмущающих сил на оси связанной системы координат ;

, , - проекции управляющих сил на оси связанной системы координат.

Параметрами движения центра масс БЛА являются кажущиеся ускорения, действующие по продольной, нормальной и боковой его осям.

Из анализа дифференциальных уравнений (4.10) следуют важные выводы.

Для измерения параметров линейного движения центра масс - кажущихся ускорений необходимо иметь на борту специальные информационно-измерительные устройства - измерители ускорений - акселерометры. Минимальное количество акселерометров определяется количеством измеряемых проекций ускорений, т.е. необходимо иметь как минимум три акселерометра.

В уравнениях (4.10) имеют место неизвестные составляющие угловой скорости относительного движения связанной системы относительно неподвижной системы координат OXYZ. Система трёх уравнений с шестью неизвестными не имеет решения с математической точки зрения и не реализуема в техническом плане.

В частном случае, когда отсутствует угловое движение БЛА, т.е.

 =0, можно реализовать систему управления и обеспечить управление полетом БЛА.

В общем случае необходимо реализовывать на борту систему стабилизации осей чувствительности акселерометров, и для этой цели измерять параметры углового движения БЛА.