3.2. Лабораторная работа № 9. Определение перемещений в стальных балках

3.2.1. Основные положения

Цель работы – экспериментальная проверка теоретических определений прогибов и углов поворота в стальных балках.

Теоретически любые перемещения можно определять методом Мора по формуле

, (3.5)

для решения которой используется графоаналитический способ Симпсона-Корноухова. При этом формула (3.5) принимает вид

(3.6)

Можно указать следующий порядок определения перемещений по формуле (3.6)

а. Строится эпюра изгибающих моментов М_F от реальной нагрузки с вычислением значений в начале участка - , в середине участка - и в конце участка - .

б. Вспомогательную балку нагружают единичной нагрузкой в точке, где требуется определить перемещение. Если определяется прогиб, то в заданном направлении прикладывают единичную силу, если определяется угол поворота, то прикладывается единичный момент.

в. Строится единичная эпюра изгибающих моментов по трем точкам каждого участка: в начале - , в середине - , в конце - .

г. Эпюры М_F и перемножаются согласно формуле (3.6), где l_i – длина участка; E_iI_i – жесткость участка балки; Е – модуль Юнга материала балки; I_x – осевой момент инерции сечения балки.

д. Если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичной нагрузки.

Перемещения определяются для двух схем балок, представленных на рис. 3.3.

Рис. 3.3. Схемы балок с примерами приложения нагрузок и мест определения перемещений

Балки загружаются только сосредоточенными силами и моментами.

Перед проведением испытаний, когда на балке нет нагрузки, стрелки индикаторов устанавливаются на нуль. Затем к балке прикладывается нагрузка и записываются показания индикаторов. Определяются значения прогибов и углов поворота сечения в местах установки индикаторов.

Угол поворота сечения измеряется при помощи специального угломера, схема которого представлена на рис. 3.3, г.

. (3.7)

Необходимо сопоставить опытные величины прогибов и углов поворота сечений балок с их теоретическими значениями и сделать вывод о справедливости применяемых формул.

При нагружении необходимо помнить, что в опасном сечении наибольшее нормальное напряжение не должно превышать значения допускаемого напряжения для материала балки

, (3.8)

где М_х - изгибающий момент в опасном сечении,

W_х - момент сопротивления при изгибе балки.

3.2.2. Теоретическое определение прогиба в двухопорной балке

Определим прогиб в середине пролета двухопорной балки, имеющей жесткость ЕI_x=const, от действия сосредоточенной силы F, приложенной в точке С (рис. 3.4, а).

Сначала определяем реакции опор R_A и R_B и строим грузовую эпюру М_F, определяя ее ординаты в трех точках каждого участка. Эпюра построена по растянутому волокну (3.4, б).

В точку К вспомогательной балки прикладываем единичную сосредоточенную силу в ожидаемом направлении прогиба (рис. 3.4, в), определяем опорные реакции и строим эпюру (рис. 3.4, г).

Рис. 3.4. К определению прогиба в середине двухопорной балки:

а – схема нагружения; б – грузовая эпюра изгибающего момента; в – вспомогательная балка с единичной сосредоточенной силой, приложенной в точке К; г – эпюра единичного изгибающего момента; д – изогнутая ось балки, прогиб в точке К и угол поворота в точке А; е - вспомогательная балка для определения угла поворота сечения А; ж – единичная эпюра

Перемножим эпюры М_F и согласно формуле Симпсона-Корноухова:

;

.

Определим угол поворота сечения А. Для этого нагрузим вспомогательную балку моментом в точке А (рис. 3.4, е). Построим единичную эпюру изгибающих моментов (рис. 3.4, ж). Перемножим эпюры М_F и :

;

; .

Знак «минус» говорит о том, что действительный угол поворота сечения А будет направлен в обратную сторону действия момента , т.е. по часовой стрелке.

3.2.3. Теоретическое определение стрелы прогиба консольной

балки от действия сосредоточенной силы

Рис. 3.5. К определению прогиба конца консоли от действия

сосредоточенной силы:

а – схема нагружения; б – изогнутая ось балки и прогиб в точке К; в – грузовая эпюра изгибающих моментов М_F; г – вспомогательная балка; д – единичная эпюра изгибающих моментов

Наибольший прогиб в консольной балке – стрела прогиба определится перемножением эпюр М_F и по рис. 3.5, в и 3.5, д.

;

.

3.2.4. Порядок выполнения работы

1. Начертить схемы балок с указанием приложенных нагрузок и мест расположения индикаторов.

2. Записать размеры b, h, l, l₁, l₂, l₃, R и величины нагрузок.

3. Вычислить 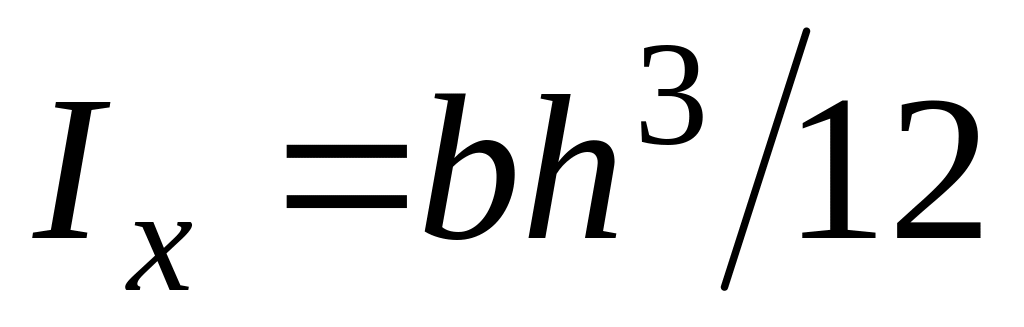, (см⁴); , (см³).

4. Вычислить теоретические значения прогибов.

5. Экспериментально определить прогибы в местах установки индикаторов.

6. Вычислить расхождения между теоретическими – Δ^Т и экспериментальными – Δ^Э значениями прогибов в процентах:

.