- •Сопротивление материалов Лабораторные работы. Часть 1
- •Сопротивление материалов Лабораторные работы. Часть 1
- •Предисловие
- •Введение
- •1. Измерительная техника и методы измерений
- •Испытательные машины
- •Машина разрывная модели р-5
- •Машина для испытаний на кручение модели км-50-1
- •Копер маятниковый км-30
- •Испытательные установки
- •Измерительные приборы и инструменты
- •Измеритель деформаций ид-70
- •Индикатор часового типа
- •Штангенциркули и микрометры
- •Методы измерений
- •Механические тензометры
- •1.4.2. Лабораторная работа № 1. Основы электротензометрии
- •1.4.2.1. Основные положения
- •1.4.2.2. Устройство тензорезисторов
- •1.4.2.3. Схемы соединения тензорезисторов для измерения деформаций
- •Контрольные вопросы и варианты ответов
- •Рекомендуемая литература:
- •2.1.2. Оборудование для испытаний
- •2.1.3. Проведение испытаний и подсчет результатов
- •2.1.4. Последовательность выполнения работы
- •Контрольные вопросы и варианты ответов
- •2.2. Лабораторная работа № 3. Испытание на сжатие
- •2.2.1. Общие сведения
- •2.2.2. Испытание на сжатие образцов из пластичной стали
- •2.2.3. Испытание на сжатие образца из серого чугуна
- •2.2.4. Испытание на сжатие древесины вдоль и поперек волокон
- •2.2.5. Испытание на сжатие искусственного (цементного) камня
- •2.2.6. Последовательность выполнения работы
- •Контрольные вопросы и варианты ответов
- •2.3.2. Порядок выполнения работы
- •Контрольные вопросы и варианты ответов
- •2.4. Лабораторная работа № 5. Испытание металлических образцов на срез
- •2.4.1. Общие сведения
- •2.4.2. Порядок выполнения работы
- •Контрольные вопросы и варианты ответов
- •2.5. Лабораторная работа № 6. Испытание стали на кручение
- •2.5.1. Общие сведения
- •450 К продольной оси стержня; τ - касательное напряжение; σ1, σ2 и σ3 - первое, второе
- •2.5.2. Порядок выполнения работы
- •Контрольные вопросы и варианты ответов
- •2.6. Лабораторная работа № 7. Тарировка проволочных тензорезисторов
- •2.6.1. Общие сведения
- •2.6.2. Порядок выполнения работы
- •Контрольные вопросы и варианты ответов
- •Рекомендуемая литература
- •3.1.2. Постановка испытания
- •Где приклеены тензорезисторы 6 и 7 (см. Рис. 3.1, а):
- •3.1.3. Порядок выполнения работы
- •Контрольные вопросы и варианты ответов
- •3.2. Лабораторная работа № 9. Определение перемещений в стальных балках
- •3.2.1. Основные положения
- •3.2.2. Теоретическое определение прогиба в двухопорной балке
- •Контрольные вопросы и варианты ответов
- •3.3. Лабораторная работа № 10. Экспериментальная проверка принципа взаимности перемещений
- •3.3.1. Основные положения
- •3.3.2. Порядок выполнения работы
- •Контрольные вопросы и варианты ответов
- •Заключение
- •Библиографический список
Контрольные вопросы и варианты ответов
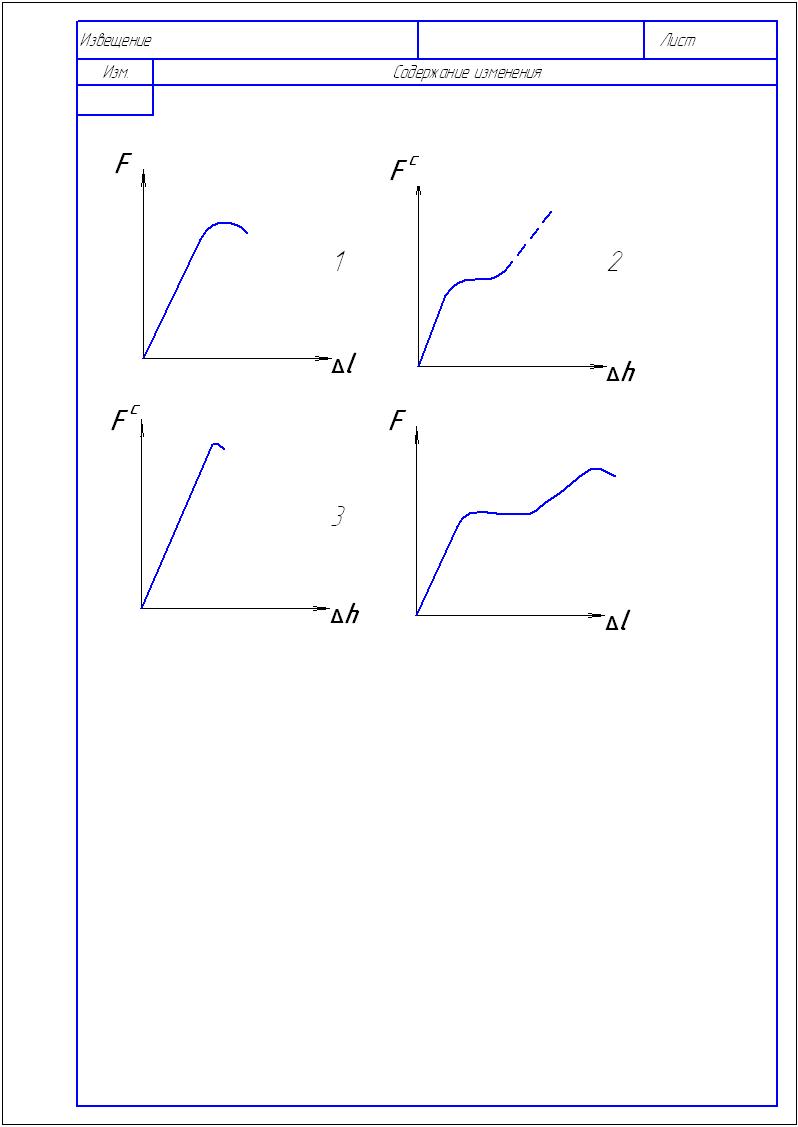
1. Какая из приведенных диаграмм является диаграммой сжатия малоуглеродистой стали: |
|||||||
|
|||||||
4 |
|||||||
2. Какие механические характеристики не определяются по диаграмме сжатия: |
|||||||
а) для пластичного материала; б) хрупких материалов? |
1)
3)
|
||||||
3. У какого из указанных материалов прочностные свойства при растяжении, сжатии практически одинаковы: |
|||||||
1) чугун; 2) камень; 3) малоуглеродистая сталь; 4) бетон. |
|||||||
4. Какой вид имеет диаграмма сжатия образца: а) из хрупкого; б) пластичного материала?
|
|||||||
5. С какой целью проводится испытание на сжатие: |
|||||||
1) определение характеристик прочности; |
|||||||
2)определение характеристики прочности и пластичности; |
|||||||
3) определение характеристик пластичности; |
|||||||
4) определение энергетической характеристики. |
|||||||
6. Какой вид имеет диаграмма сжатия образца: а) из малоуглеродистой стали; б) чугуна; в) дерева вдоль волокон; г) дерева поперек волокон. |
|||||||
|
|||||||
7. Какие характеристики прочности материала не могут быть определены по приведенной диаграмме сжатия: |
1) ; 2) ; 3) ; 4) . |
|
|||||
8. Какие характеристики прочности материала не могут быть определены по приведенной диаграмме сжатия: |
1) ; 2) ; 3) ; 4) . |
|
|||||
9. Какие механические характеристики могут быть определены по диаграмме сжатия: |
|||||||
а) для пластичного материала; б) хрупкого материала. 1) ; 2) ; 3) ; 4) . |
|||||||
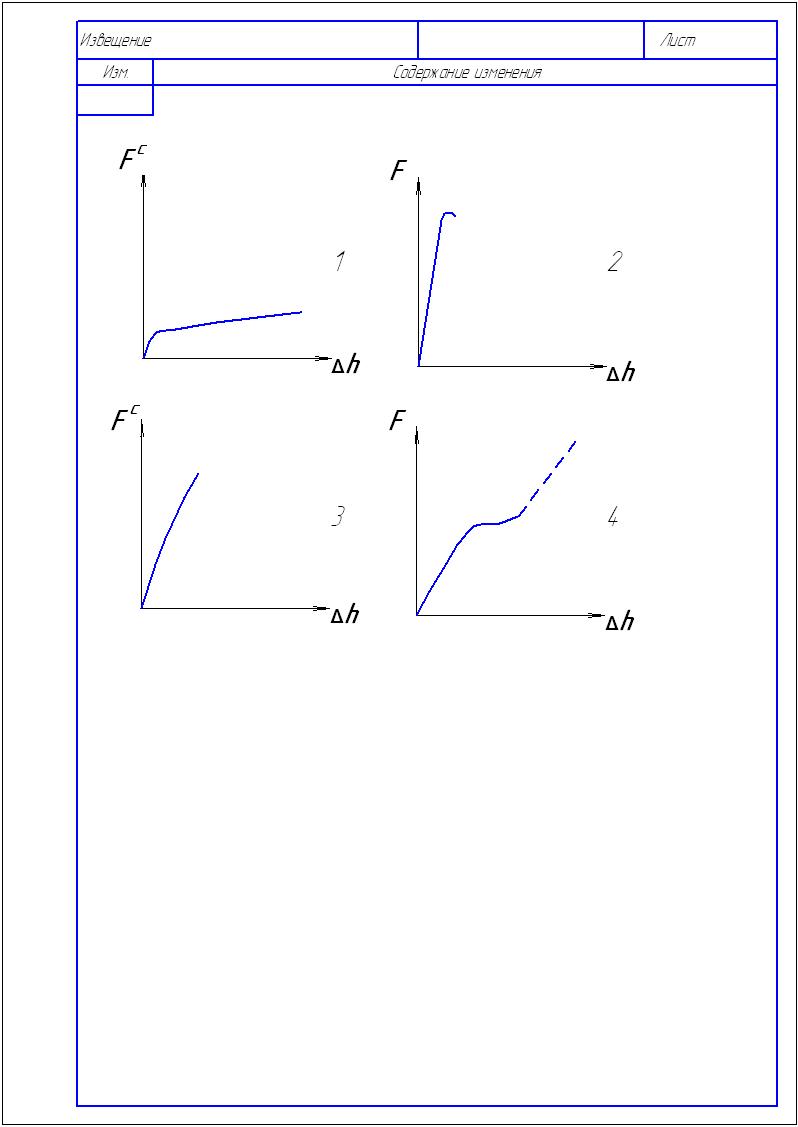
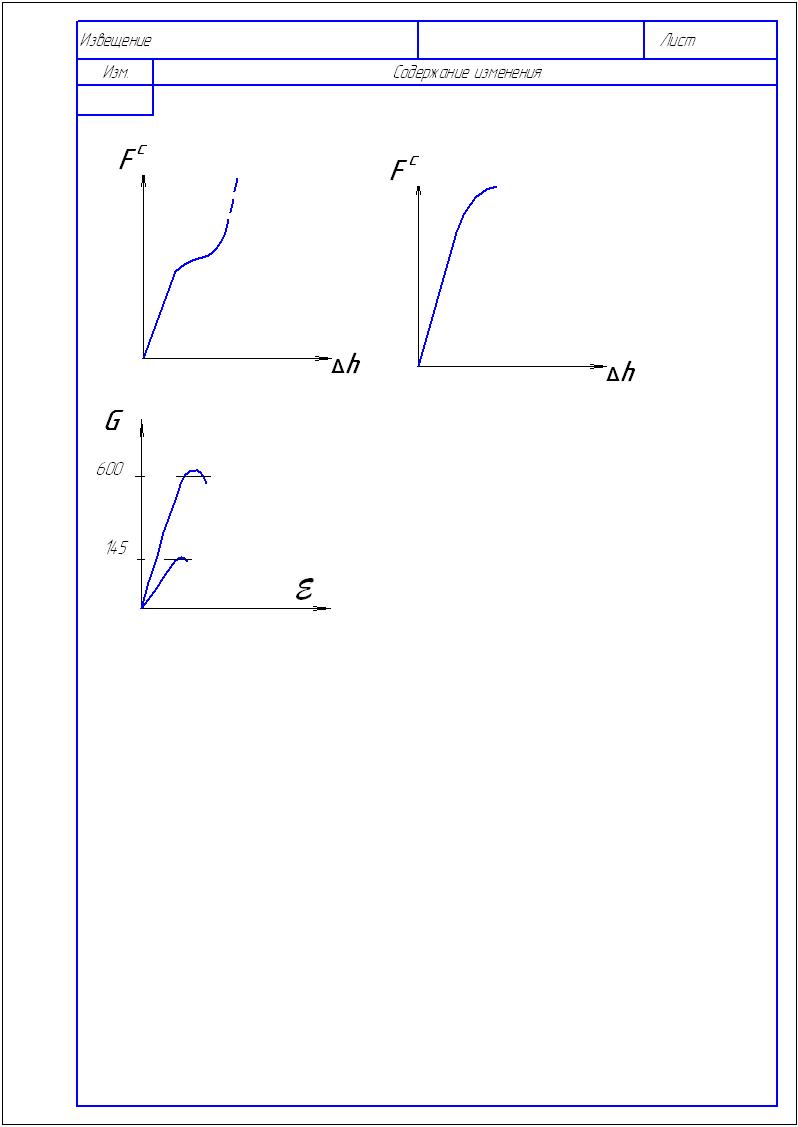
10. На рисунке показаны две диаграммы испытания серого чугуна. Какая из них является диаграммой сжатия? |
|||||||
|
|
||||||
11. Предел текучести для пластичного материала: |
|||||||
1) одинаков при растяжении и сжатии; |
|||||||
2) больше при растяжении; |
|||||||
3) больше при сжатии; |
|||||||
4) не определяется ни при сжатии, ни при растяжении. |
|||||||
12. Основной характеристикой прочности хрупких материалов при сжатии является: |
|||||||
1) предел пропорциональности; 2) предел упругости; 3) физический предел текучести; 4) предел прочности. |
|||||||
13. При испытании каких материалов на диаграмме сжатия имеет место площадка текучести: 1) чугун; 2) малоуглеродистая сталь; 3) цементный камень; 4) древесина вдоль волокон. |
|||||||
14. Какую характеристику прочности принято считать предельным (опасным) напряжением: |
1) временное сопротивление;
|
||||||
а) для пластических; |
4) предел пропорциональности. |
||||||
б) хрупких материалов. |
|||||||
15. Что называется: а) прочностью; б) жесткостью; в) устойчивостью; г) пластичностью. |
1) способность тела сопротивляться деформациям; 2) способность тела сопротивляться разрушению; 3) способность тела сохранять свою первоначальную форму равновесия; 4) способность материала получать большие остаточные деформации, не разрушаясь. |
||||||
2.3. Лабораторная работа № 4. Определение модуля
упругости и коэффициента Пуассона для стали
при растяжении
2.3.1. Общие сведения
Цель работы - экспериментальное определение величин модуля упругости Е (модуля Юнга) и коэффициента Пуассона μ для стали и сравнение их с табличными значениями.
Для модуля упругости Е и коэффициента Пуассона μ при растяжении
стального образца в области упругих деформаций, когда справедлив закон Гука, можно записать формулы:
![]() ;
;
![]() ,
(2.16)
,
(2.16)
где
![]() -
нормальное напряжение;
-
нормальное напряжение;
N – продольное внутреннее усилие от приложенной растягивающей осевой нагрузки F, Н (N = F);
А0 – площадь поперечного сечения, мм2;
ε и ε' – соответственно относительные продольная и поперечная деформации;
«–»обозначает, что ε' при растяжении меньше нуля;
μ = 0,25-0,35 - табличные значения для всех металлов. Величина μ характеризует свойства материала и определяется экспериментально;
Е = (1,9-2,1)1011 Па = (1,9-2,1)1011 Н/м2 = (1,9-2,1)105 МПа = (1,9-2,1)105 Н/мм2 =
= (1,9-2,1)104 кН/см2 - табличное значение для стали.
Модуль упругости можно определить, преобразовав закон Гука
![]() ,
(2.17)
,
(2.17)
где ∆F - приращение нагрузки,
∆εср - среднее приращение относительной продольной деформации образца от действия ∆F при количестве ступеней испытания равном m.
Коэффициент Пуассона находится по формуле
![]() ,
(2.18)
,
(2.18)
где ∆ε' - среднее приращение относительной поперечной деформации образца от действия ∆F при количестве ступеней испытания равном m.
Испытание проводится на плоском образце прямоугольного поперечного сечения с помощью метода электротензометрии. Тензодатчики (тензорезисторы) наклеены на образец таким образом, что датчики 1 и 2 регистрируют продольные деформации, а датчики 3 и 4 - поперечные деформации (рис. 2.8). Рабочие тензорезисторы 1, 2 и 3, 4 подсоединены к двум парам компенсационных датчиков такой же базы и образуют два измерительных моста. С помощью первого моста можно определить продольные деформации образца, а с помощью второго - поперечные. Мосты подключены к измерителю деформаций ИД-70 (рис. 2.8, в). Образец растягивается на машинах Р-5 или УММ-5.
в
б
а
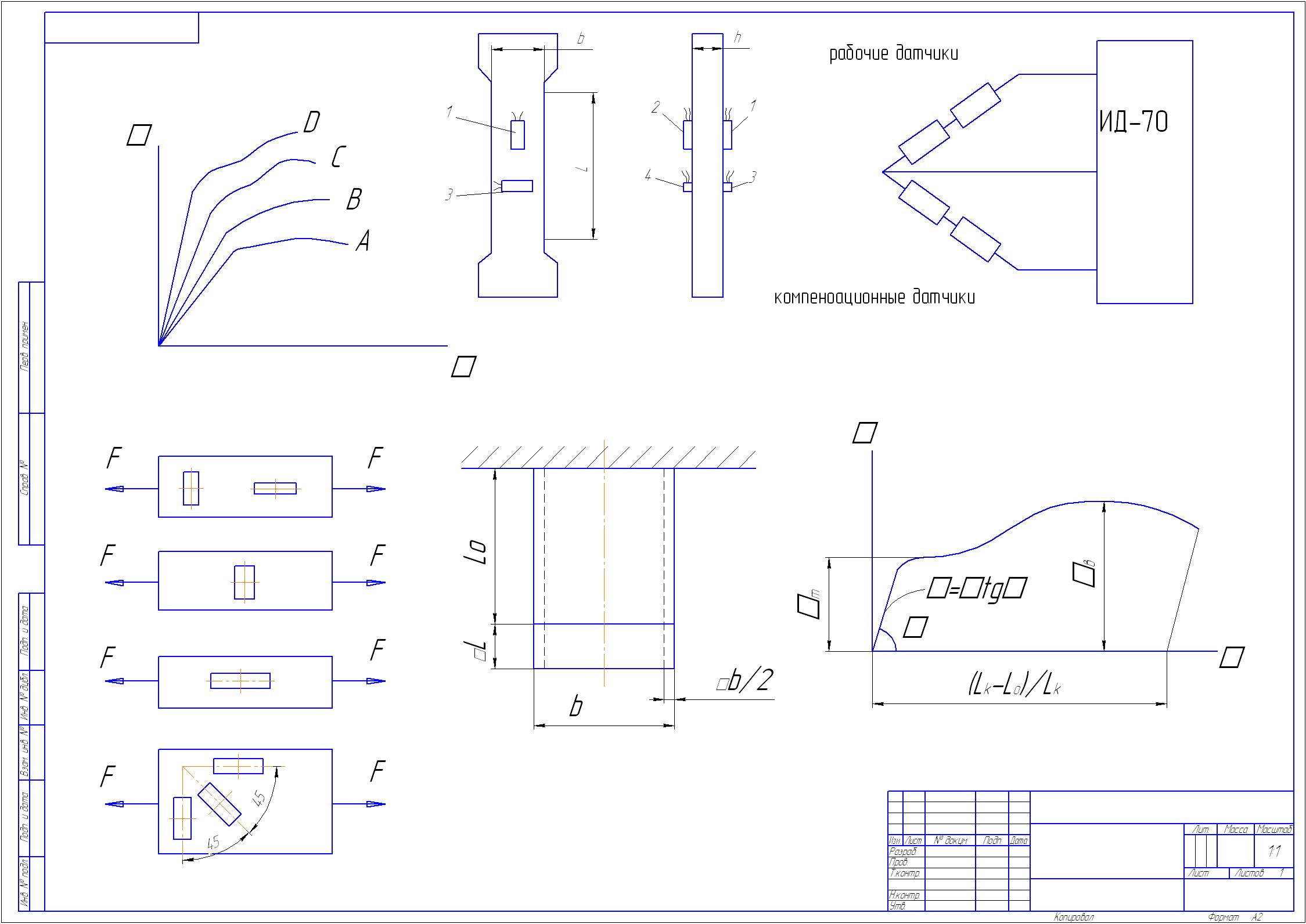
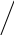



Рис. 2.8. К испытанию плоского образца:
а, б - два вида образца с поперечным сечением bхh, L - рабочая длина образца; в - схема измерения; 1,2 и 3,4 - датчики, регистрирующие продольные и поперечные деформации