Лабораторная работа №7. Энтропия источника непрерывных сообщений
Непрерывный
сигнал
,
принимает бесконечное множество
возможных значений на интервале
.
Вероятность появления конкретного
значения
,
бесконечно мала, вследствие бесконечного
количества их возможных значений. Пусть
– плотность вероятности сигнала
на интервале
.
Для
получения значения энтропии сигнала
разделим область изменения сигнала
на
интервалов с равномерным шагом
(см. рис. 7.1). Вероятность нахождения
сигнала в интервале от
до
соответственно будет равна
.
В случае если рассмотреть дискретный
источник, где в качестве сообщения будем
рассматривать факт нахождения значения
на интервале
,
то по (7.__) энтропия источника непрерывных
сообщений будет равна
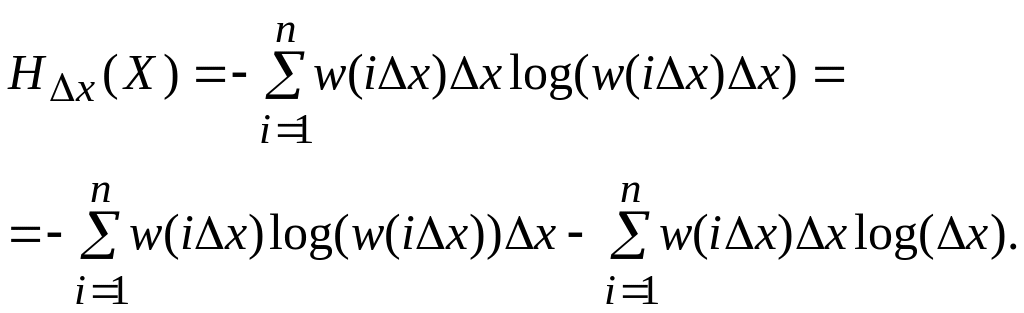(7.1)
При
переходе
и так как
,
получим
. (7.2)
Таким образом, энтропия непрерывного источника сообщений равна бесконечности.
Первую часть выражения (2.26) можно рассматривать как дифференциальную энтропию непрерывного источника сообщений:
. (7.3)
Значение
показывает степень неопределенности
различных процессов. Исходя из (2.27)
значение дифференциальной энтропии
может быть
.
Максимальное значение достигается при нормальном распределении сигнала []. Для с дисперсией значение
. (7.4)
Выполнение лабораторной работы
Этап I
Запустить программу лабораторной работы TIPSlab7.exe. Выбирая различные сигналы, их параметры, суммы сигналов изучить значения дифференциальной энтропии. Найти для каких сигналов дифференциальная энтропия будет иметь максимальное значение.
Исследовать
влияние шага расчета дифференциальной
энтропии
на получаемые значения.
Внешний вид и пример результатов исследования показан на рис. 7.1.
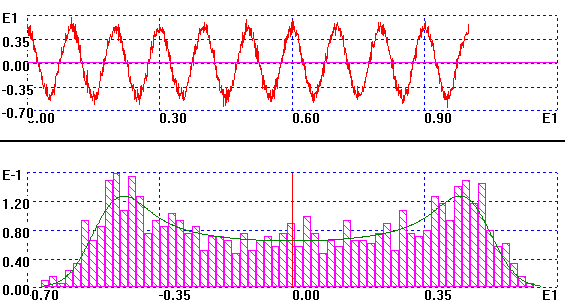
Рис. 7.1. Внешний вид программы и результаты исследования значений дифференциальной энтропии
Этап II
Реализовать программу вычисления дифференциальной энтропии в MatLab.
Сформировать массив, содержащий сигнал, выбранный Вами в программе лабораторной работы. Для построения сигнала с нормальным законом распределения Вам рекомендуется сложить несколько процессов с равномерным законом распределения:
.
По полученному массиву Вам необходимо построить гистограмму процесса и по (7.3) рассчитать значение дифференциальной энтропии.
Содержание отчета
Отчет по лабораторной работе должен содержать:
Виды сигналов и плотности распределения исследуемых в программе лабораторной работы сигналов и значения дифференциальной энтропии этих сигналов.
График и плотность распределения процесса, построенного в MatLab.
Листинг сеанса MatLab.
Рассчитанное значение дифференциальной энтропии.
Выводы о том, какие свойства сигналов больше влияют на значение дифференциальной энтропии.
Лабораторная работа №7. Линейные коды
В лабораторной работе исследуются линейные коды, получившие большое распространение на практике. Линейным двоичным кодом называется код, для которых сумма по модулю два любых разрешенных кодовых комбинаций является разрешенной кодовой комбинацией.
Линейный код является систематическим,
если
символов его являются информационными,
а
символов являются проверочными (
–
длинна кодовой последовательности).
Линейный код обозначают
и его можно записать как:
Избыточность линейного кода определяется как:
.
Для примера рассмотрим код (8,4), проверочные символы которого формируются следующим образом:
.
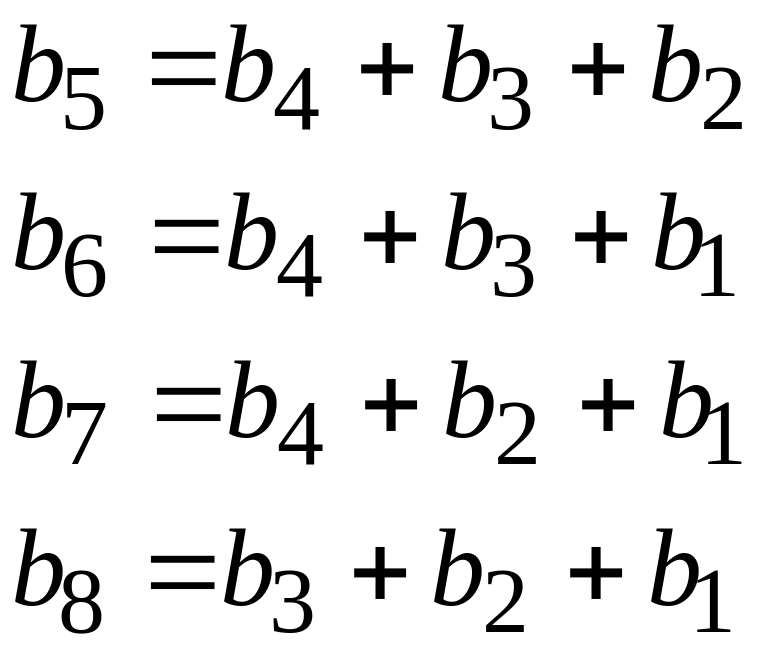Например,
при передачи символа
,
кодовая последовательность будет имеет
значение:
.
Получатель
сообщения примет последовательность
.
Вследствие ошибки в канале принятая
последовательность может отличатся от
переданной последовательности:
.
В этом случае выбирается комбинация
наиболее близкая по расстоянию по
Хеменгу из числа всех возможных
комбинациях.
Например, при передаче рассмотренной выше последовательности возникли ошибки, результаты сравнения приведены в табл.7.1.
Табл. 7.1. Пример работы линейного кода (8,4)
Переданная
последовательность
|
0 1 0 0 1 0 1 1 |
0 1 0 0 1 0 1 1 |
0 1 0 0 1 0 1 1 |
|
Ошибка |
0 0 0 0 0 0 0 0 |
0 0 0 0 0 0 0 1 |
1 0 0 0 0 0 0 1 |
|
Принятая последовательность |
0 1 0 0 1 0 1 1 |
0 1 0 0 1 0 1 0 |
1 1 0 0 1 0 1 0 |
|
Все возможнее комбинации кода |
Расстояние по Хеменгу между переданной и принятой последовательностью |
|||
|
|
|
|
|
0 |
0 0 0 0 0 0 0 0 |
4 |
3 |
4 |
1 |
0 1 1 1 1 0 0 0 |
4 |
3 |
4 |
2 |
1 0 1 1 0 1 0 0 |
8 |
7 |
6 |
3 |
1 1 0 0 1 1 0 0 |
4 |
3 |
2 |
4 |
1 1 0 1 0 0 1 0 |
4 |
3 |
2 |
5 |
1 0 1 0 1 0 1 0 |
4 |
3 |
2 |
6 |
0 1 1 0 0 1 1 0 |
4 |
3 |
4 |
7 |
0 0 0 1 1 1 1 0 |
4 |
3 |
4 |
8 |
1 1 1 0 0 0 0 1 |
4 |
5 |
4 |
9 |
1 0 0 1 1 0 0 1 |
4 |
5 |
4 |
10 |
0 1 0 1 0 1 0 1 |
4 |
5 |
6 |
11 |
0 0 1 0 1 1 0 1 |
4 |
5 |
6 |
12 |
0 0 1 1 0 0 1 1 |
4 |
5 |
6 |
13 |
0 1 0 0 1 0 1 1 |
0 |
1 |
2 |
14 |
1 0 0 0 0 1 1 1 |
4 |
5 |
4 |
15 |
1 1 1 1 1 1 1 1 |
4 |
5 |
4 |
Декодирование |
Верно |
Верно |
Невозможно |
|
При реализации декодера все возможные комбинации кода записываются в ПЗУ. Формируемые полиномы в кодере, так же обычно представляются в виде двоичной матрицы. Для рассмотренного примера эта матрица имеет значение:
.
Процесс кодирования в этом случае выглядит следующим образом:
.
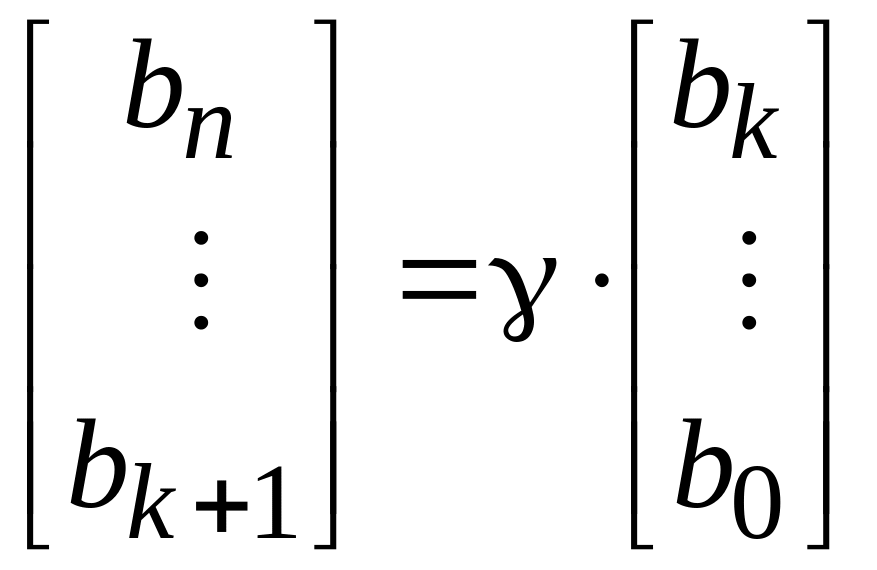К недостаткам линейных кодов можно отнести необходимость хранения больших массивов чисел.