Лабораторная работа 7. Определение рационального числа постов для оказания услуги методами теории массового обслуживания

7.1. Общие положения

Критериями качества и эффективности работы сервисного предприятия полнота загрузки его производственных мощностей при минимальных размерах очередей потребителей услуг.

Можно менять произ­водительность оказания услуги с помощью резервного персонала и оборудования, выделенного определенным пунктам обслуживания, чтобы предотвратить или сократить оче­реди. По мере того как обслуживание улучшается (а именно — ускоряется), стоимость времени, потраченного на ожидание в очереди, снижается. Издержки ожидания могут отражать потерянную производительность работников, когда их инструменты или станки нуждаются в ремонте, или просто могут быть оценкой издержек потребителей, понесенных из-за плохого обслуживания и длинной оче­реди.

Системы обслуживания обычно классифицируются с позиций количества кана­лов (т. е. количества постов обслуживания) и количества фаз (т. е. количества ос­тановок в обслуживании, которые необходимо сделать).

Однофазовые системы — это те, в которых потребитель получает услугу только в одном пункте и покидает систему. Модели массового обслуживания помогают принять решения, чтобы уравновесить затраты на требуемый объем деятельности с затратами на ожидание в очереди. Вот некоторые оценки обслуживания очередей, полученные в резуль­тате анализа образования очередей:

- среднее время, которое каждый потребитель или объект проводит в очереди;

- средняя длина очереди;

- среднее время, которое каждый потребитель проводит в системе (время ожидания плюс время обслуживания);

- среднее количество потребителей в системе;

- вероятность, с которой средство обслуживания будет простаивать;

- коэффициент использования системы;

- вероятность нахождения определенного количества потребителей в системе.

7.2 Одноканальная модель массового обслуживания

На рисунке 3 представлена одноканальная модель массового обслуживания потребителей

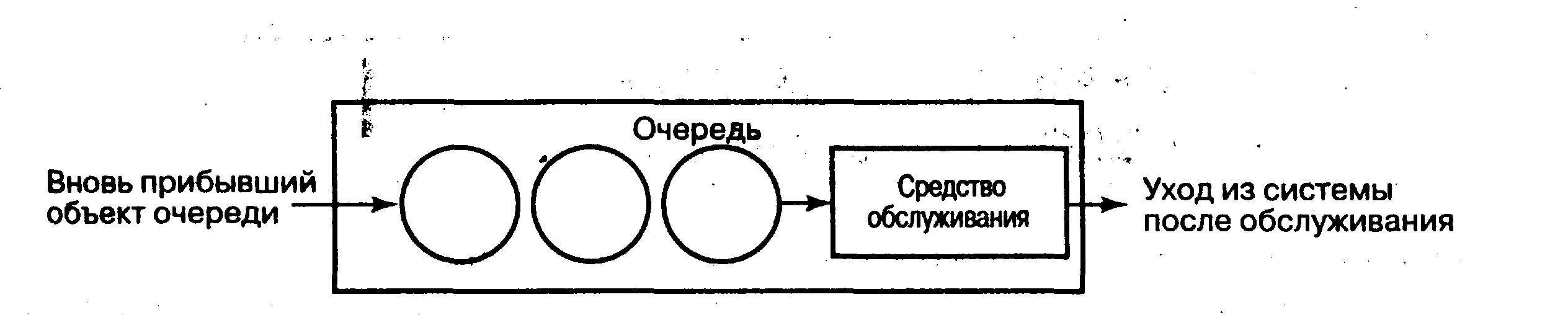
Рисунок 3. Одноканальная система массового обслуживания потребителей

Обычный пример массового обслуживания — это одноканальная или одноузло­вая очередь. Вновь прибывшие объекты формируют единую очередь, чтобы их обслужили на одном пункте. В этом типе системы обычно бывают следующие условия:

- вновь прибывшие обслуживаются в порядке прибытия, по принципу «первым прибыл — первым обслужили», каждый вновь прибывший ждет своей очереди независимо от длины очереди,

- вновь прибывшие клиенты независимы от прибывших раньше, но среднее количе­ство объектов в очереди (интенсивность входного потока) не меняется во времени,

- интенсивность входного потока описывается пуассоновским распределе­нием вероятности, и объекты поступают из бесконечной (или очень боль­шой) совокупности,

- периоды времени обслуживания меняются от одного потребителя к друго­му и не зависят друг от друга, но их среднее значение известно,

- время обслуживания изменяется согласно отрицательному, экспоненци­альному распределению вероятности,

- средняя интенсивность обслуживания больше, чем средняя интенсивность входного потока.

Когда эти условия соблюдены, можно применять формулы, позволяющие рассчитать семь оценок обслуживания очередей, описанных выше. Вычисления по этим формулам основаны на общих показателях среднего количества вновь прибывших объектов за период времени (λ) и среднего количества потребителей, обслуженных за период времени (μ). Следующий при­мер иллюстрирует, как можно применять одноканальную модель.

Слесарь шиномонтажного участка, может ремонтировать колеса со средней скоростью три колеса в час (или один примерно за 20 минут) в соответствии с отрицательным экспоненци­альным распределением. Клиенты, нуждающиеся в этой услуге, прибывают в ма­стерскую в среднем два человека в час, следуя пуассоновскому распределению. Клиенты обслуживаются по принципу «первым прибыл — первым обслужили» и поступают из очень большой совокупности возможных потребителей.

Из этого описания мы можем взять операционные характеристики системы массового обслуживания шиномонтажного участка:

λ = 2 машины, поступающие в час;

μ = 3 машины, обслуживаемые в час;

λ 2

L_s = —— = —— = 2 машины в системе в среднем

μ – λ 3 - 2

1 1

W_s= —— = ——=1час;

μ - λ 3-2

Т.е. 1 час — среднее время ожидания в системе.

L_q = λ² / μ(μ – λ) = 2² / 3(3 – 2) = 1,33 машин, ожидающих в очереди в среднем

W_q = λ / μ(μ – λ) = 2 / 3(3 – 2) = 2/3

40 минут среднего времени ожидания в очереди на одну машину.

ρ = λ / μ = 2/3, т.е. 66,6% времени занятости механика.

P_о = 1 – λ / μ = 1 – 2/3 , т.е.0,33 вероятность того, что в системе 0 потребителей

.

Р_n>3 = (λ / μ)^k+1 = (2 /3)¹⁺³ , т.е.0,198, или 19,8%, вероятность того, что в системе больше 3 машин.

Когда операционные характеристики системы массового обслуживания подсчи­таны, важно провести экономический анализ их влияния. Модель линии обслужи­вания, описанная выше, очень полезна при прогнозировании времени ожидания, длины очередей, времени простоя и т. д., но она не определяет оптимального реше­ния или значительных факторов затрат. Решение пробле­мы образования очередей может потребовать от руководства выбора между ростом издержек обеспечения лучшего обслуживания и снижением издержек ожидания, вторичных по отношению к обеспечению этого обслуживания.