4.1.2 Метод обращённой (обратной) матрицы.
Метод обращения матрицы может быть использован для решения СЛАУ, но только для задач, где исходная матрица не изменяется, а решение надо найти для многих правых столбцов . Данный метод достаточно затратный (требует много машинного времени). Поскольку при обращении матрицы реализованы алгоритмы аналогичные методу Крамера.
4.1.3 Метод Гаусса.
Наибольшее распространение из простых алгоритмов получил метод Гаусса. Идея метода проста и заключается в последовательном исключении неизвестных в строках матрицы. В простом методе Гаусса преобразование начинается по порядку следования уравнений.
Наиболее часто реализуется алгоритм решения СЛАУ по методу Гаусса с выборкой главных (ведущих) элементов.
Задание на лабораторную работу №2
Реализовать алгоритм метода Гаусса и решить с его помощью систему 5х5.
Сравнить полученные результаты с результатами работы подпрограммы решения СЛАУ из библиотеки IMSL.
4.2 Итерационные методы решения слау.
Данные методы были разработаны для
решения больших систем СЛАУ. Если порядок
системы
точные методы предпочтительнее по
времени вычисления. Если порядок системы
итерационные методы сопоставимы, если
.
То итерационные методы в 2 раза быстрее.
4.2.1 Метод простой итерации.
Рассмотрим СЛАУ с невырожденной матрицей
(
)
или в матричной форме:
Исходная задача преобразуется к эквивалентному виду
.
Здесь
,
.
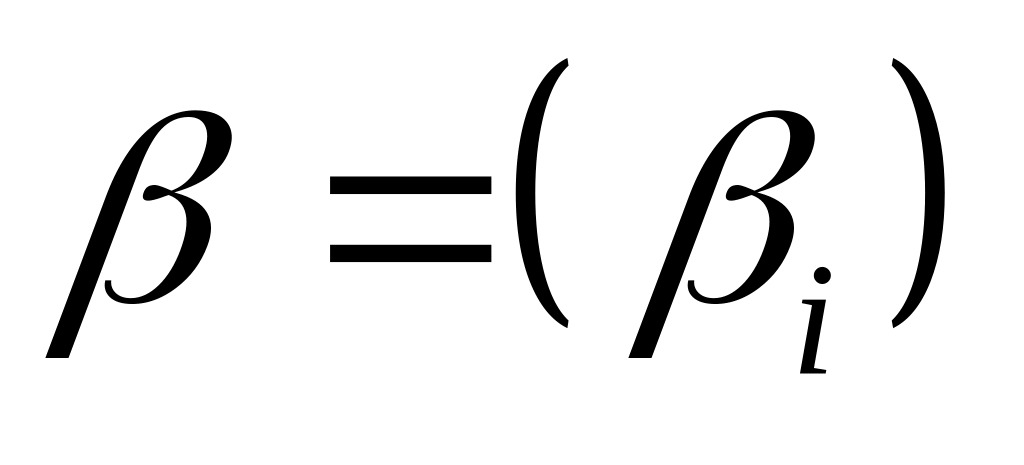Такое преобразование выполняется
различными путями с тем условием, что
.
Наиболее распространённым способом
приведения системы к эквивалентному
виду является следующий:
;
,
где
,
,
,
где
При использовании данной процедуры метод простых итераций называется методом Якоби.
В нулевом приближении за
вектора неизвестных обычно принимается
вектор правых частей
.
Тогда итерационный процесс будет
выглядеть как:
В методах итерационных процедур вводится понятие требуемой точности, она назначается программистом (пользователем):
4.2.2 Метод итераций Зейделя.
В методе Зейделя итерации организованы таким образом , что на каждом последующем шаге в последующем уравнении дополнена информация о всех уже найденных уравнениях.
Рассмотрим итерацию
:
Такой метод позволяет существенно сократить время нахождения решений по сравнению с простой итерацией.
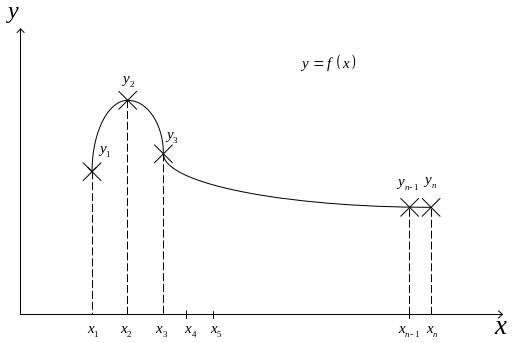
4. Задачи интерполяции и аппроксимации таблично заданной функции.
В задачах сплошности очень часто приходится рассчитывать значение некой функции, которая задана в виде таблиц.
В этом случае для нахождения значения функции (неизвестной) решается две задачи:
интерполяция функции;
аппроксимация функции.
интерполяция аппроксимация
