Донецкий институт железнодорожного транспорта

Харьковская государственная академия железнодорожного транспорта

Кафедра автоматики, телемеханики, связи и вычислительной техники.

Методические указания

по курсовому проектированию

для студентов специальности АТ

по курсу "Электроника и микросхемотехника"

Донецк 2004

1. Задачи курсового проектирования

Курсовое проектирование является завершающим зтапом изучения студентами курса «Электроника и микросхемотехника» и имеет целью:

- систематизировать и закрепить знания студентов в области

разработки злектронных устройств;

- научить студентов самостоятельно пользоваться технической литературой, справочниками, стандартами и другой нормативной документацией;

- научить студентов самостоятельно решать задачи, связанные с

разработкой и расчетом злектронных устройств.

Работа над курсовым проектом подготавливает студентов к будущему дипломному проектированию.

2. Содержание и объем курсового проекта

Курсовой проект состоит из пояснительной записки и чертежей (графической части).

Объем пояснительной записки и графической части должен составлять не менее 20 стр. Курсовой проект, как правило, содержит следующие структурные злементы:

1. Титульний лист (см. приложение 1).

2. Реферат.

3. Индивидуальное задание.

4. Содержание.

5. Введение.

6. Основная часть.

7. Дополнения.

8. Заключение.

9. Список использованной литературы.

Оформление курсового проекта должно соответствовать требованиям, изложенным в методическом пособии по вьіполнению и оформленню курсовых и дипломных работ.

В реферате описывается цель и очень краткое содержание курсового проекта. Здесь же приводится количество страниц, рисунков, дополнений, а также список ключевых слов.

Введение должно содержать анализ места и значения цифровых устройств в современной электронике, краткие теоретические сведения о способах решения задачи и о применяемых элементах цифровой микроэлектроники.

Основная часть включает задание и его подробное решение. Выполнение каждого задания должно завершаться чертежом принципиальной схемы цифрового устройства, выполненного на миллиметровой бумаге размером 210х290 мм² . Перечень злементов, схемы оформляется на отдельных листах формата А4. К последнему заданию следует вичертить эпюры напряжений на выходах триггеров, составляющих счетчик.

3. Указания к выполнению курсового проекта

Выполнение курсового проекта следует выполнять в следующем порядке:

1. Изучить курс лекций "Цифровая электроника", рекомендуемую литературу и настоящее пособие.

2. Определить свой вариант задания на курсовой проект.

3. Решать последовательно задачи своего варианта. После разработки схем их следует проверить на правильность, используя программу WorkBench.

4. Краткие теоретические сведения.

Для описания алгоритмов работы цифровых устройств Джордж Буль создал специальный математические аппарат. Булева алгебра оперирует двумя понятиями – истина и ложь, что соответствует цифрам в двоичной системе счисления единице и нулю.

Над булевыми переменными возможны различные логические операции и функциональные преобразования.

Среди множества операций, выполняемых над булевыми переменными, основными являются операции логического отрицания, сложения и умножения.

Логическое отрицание или инверсия некоторой логической переменной, например переменной х, это также логическая переменная, принимающая значение обратное значению переменной х, и обозначаемая как

_

х. Постулаты операции отрицания:

_

если х=0, то х=1

_

и наоборот если х=1, то х=0.

Дизъюнкция (логическое сложение) или функция ИЛИ (OR) - это функция f(x1, x2), которая истинна тогда, когда истинна хотя бы одна из ее переменных. Постулаты операции сложения:

х1	х2	х1+х2
0	0	0
0	1	1
1	0	1
1	1	1

Число аргументов функции ИЛИ может быть и более двух. Их количество ставится перед обозначением функции, например, 3ИЛИ.

Конъюнкция (логическое умножение) или функция И (AND) - это функция f1(x1, x2), которая истинна тогда, когда все ее переменные одновременно истинны. Постулаты операции умножения:

х1	х2	х1х2
0	0	0
0	1	0
1	0	0
1	1	1

Законы булевой алгебры вытекают из постулатов и отражают связи, существующие между логическими операциями. Большинство из них хорошо известны из школьной алгебры.

При преобразовании ФАЛ следует особо обратить внимание на правило де Моргана: ____ _ _ _____ _ _

х1х2 = х1 + х2 х1+х2 = х1 * х2

При выполнении алгебраических действий следует придерживаться строгого порядка: если в выражении отсутствуют скобки, первыми выполняются операции инверсии, затем конъюнкции и последними – операции дизъюнкции.

Способы записи ФАЛ.

Рассмотрим некоторое логическое устройство, на входе которого присутствует n-разрядное двоичное число (двоичный код), а на выходе – m-разрядный код. Для математического описания работы устройства необходимо определить зависимость каждой из m выходных переменных у от входного двоичного кода.

х1 у1

х2 Логическое у2

хn устройство уm

Зависимость выходных переменны у, выраженная через совокупность входных переменных х1,х2,…хn с помощью операций алгебры логики, носит название функции алгебры логики (ФАЛ). Понятие ФАЛ является базовым в алгебре логики. Для описания ФАЛ используются различные формы: словесная, табличная, алгебраическая, последовательность десятичных чисел и кубических комплексов.

Пример словесного описания для функции 3ИЛИ: логическая функция трех переменных равна единице, если одна из переменных равна единице.

Описание ФАЛ из предыдущего примера в виде таблицы истинности:

х1	х2	х3	У
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

Таблица для описания функции n переменных содержит 2ⁿ строк. Соответственно функция n аргументов имеет 2ⁿ наборов переменных. Количество столбцов равно сумме чисел n+m. В данном случае (всего одна выходная переменная): 3+1=4 столбца.

Описание ФАЛ в виде последовательности десятичных чисел легко понять на примере. Возьмем за основу таблицу истинности предыдущего примера. Первое значение у=1 функция имеет на наборе 001. Переводят этот двоичный код в десятичный –1. Следующая единица: 010 2, и т.д. Полученная ФАЛ записывается в следующем виде:

у(х1,х2,х3) = (1,2,3,4,5,6,7).

На некоторых этапах разработки логических устройств удобно ФАЛ представлять координатным (графическим) способом. При небольшом количестве аргументов (n<6), наиболее распространенным из них является метод карт Карно. Карта Карно представляет собой двухкоординатную таблицу – несколько видоизмененную таблицу истинности. 2ⁿ наборов, представленных соседними клетками, отличаются значением только одной переменной.

Правила построения Карно следующие:

1)Количество клеток равно количеству строк таблицы истинности.

2)Слева и сверху располагаются значения аргументов. Порядок размещения аргументов таков, что в двух соседних по горизонтали и вертикали клетках отличается значение только одного аргумента (поэтому соседними считаются и клетки, находящиеся на противоположных краях таблицы).

3)В клетки заносятся соответствующие значения ЛФ.

На рис.3 приведена карта Карно для функции 3ИЛИ.

х2х3	00	01	00	10
х1
0	0	1	1	1
1	1	1	1	1

Для разработки схем, реализующих различные логические функции, наиболее удобным является описание ФАЛ в аналитической форме, в которой ФАЛ имеет вид алгебраического выражения.

Различают две формы написания ФАЛ алгебраическим выражением ДНФ и КНФ.

Дизъюнктивной нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его инверсия входит один раз. Произведения элементарны, если они без скобок. Пример элементарных произведений (элементарных конъюнкций) :

у(х1,х2,х3) = х1х2+х1х3+х1х2х3

При проектировании устройств чаще имеют дело с совершенной дизъюнктивной нормальной формой (СДНФ). Получают СДНФ из таблиц истинности следующим образом:

• для каждого набора входных переменных на котором ФАЛ равна единице записывают конституенты единицы - элементарные конъюнкции, причем переменные, равные нулю, записывают с инверсией.

• логически суммируют полученные конституенты единицы.

Запись СДНФ для функции 3ИЛИ сделаем, воспользовавшись ее табличным представлением.

у(х1,х2,х3) = х1х2х3+х1х2х3+х1х2х3+х1х2х3+

+х1х2х3+х1х2х3+ х1х2х3

Вторая форма записи ФАЛ – это конъюнктивная нормальная форма (КНФ).

Конъюнктивной нормальной формой называется логическое произведение элементарных логических сумм, в каждую из которых аргумент или его инверсия входит один раз.

Аналогично, существует совершенная конъюнктивная нормальная форма (СКНФ).

Получают СКНФ из таблиц истинности следующим образом:

• для каждого набора входных переменных на котором ФАЛ равна нулю записывают конституенты нуля - элементарные логические суммы входных переменных, причем переменные, равные единице, записывают с инверсией.

• логически перемножают полученные конституенты нуля.

Запись СКНФ для функции 3ИЛИ сделаем, воспользовавшись ее табличным представлением.

у(х1,х2,х3) = х1+х2+х3.

Простейшие функции алгебры логики.

Кроме приведенных выше трех элементарных логических функций практический интерес представляют еще 13. В таблице приведены 16 простейших функций двух переменных х1 и х2.

Функ-ции	х1х2				Обозначение функции
	00	01	10	11
F0	0	0	0	0	константа нуль
F1	0	0	0	1	конъюнкция (и) - х1х2
F2	0	0	1	0	запрет первого аргумента - х1х2
F3	0	0	1	1	повторение первого аргумента – х1
F4	0	1	0	0	запрет второго аргумента - х1х2
F5	0	1	0	1	повторение второго аргумента – х2
F6	0	1	1	0	сложение по модулю 2 (исключающее или)- х1х2+ х1х2
F7	0	1	1	1	дизъюнкция (или) – х1+х2
F8	1	0	0	0	функция Пирса (или-не) – х1+х2
F9	1	0	0	1	равнозначность (искл. или-не)
F10	1	0	1	0	инверсия x2 (не)
F11	1	0	1	1	импликация от 1-го до2-го – х1+х2
F12	1	1	0	0	инверсия x1 (не)
F13	1	1	0	1	импликация от 2-го до1-го – х1+х2
F14	1	1	1	0	функция Шеффера (и-не) – х1х2
F15	1	1	1	1	константа единица

Логические функции и логические элементы.

Вводя понятие логической функции, мы представляли логическое устройство, реализующее эту функцию, в виде «черного ящика». В действительности устройство состоит из набора электронных схем, причем вид логической функции и состав набора схем связаны определенным образом. Аналогично тому, как сложное логическое выражение можно составить из элементарных функций, сложное логическое устройство можно представит в виде комбинации элементарных логических элементов (схем). Соответственно каждой элементарной ФАЛ можно сопоставить электронную схему (логический элемент - ЛЭ). В таблице приведены некоторые простейшие ФАЛ и эквивалентные логические элементы.

Функция	Имя ф-ции	Запись	Графическое обозначение ЛЭ
F1	и	х1х2	&
F6	исключающее или	х1х2+ х1х2	. м2
F7	или	х1+х2	1
F8	или не	х1+х2	1
F10	не	х1	1
F14	и-не	х1х2	&

Полная система логических функций. Понятие о базисе

 

Функционально полная система представляет собой набор логических функций, с помощью которых можно записать любую, сколь угодно сложную функцию. В этом случае говорят, что этот набор образует базис.

В соответствии с принципом двойственности любое сложное устройство можно реализовать в двух базисах:

    1) "И-НЕ" (базис Шеффера)

2) "ИЛИ-НЕ" (базис Пирса или функция Вебба).

 

Примеры реализации логических операций в базисах “И-НЕ” и “ИЛИ-НЕ”.

               

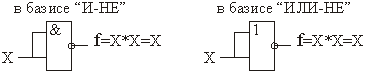
Реализация операции “НЕ”:

Для реализации функции И сделаем следующие преобразования:

у=х1х2  у=х1+х2 = х1х2. Откуда видно, как И можно реализовать в обоих базисах:

            

1

х1х2 & х1х2

1 х1+х2

&

1

Реализация операции И в базисе И-НЕ и ИЛИ-НЕ.

          

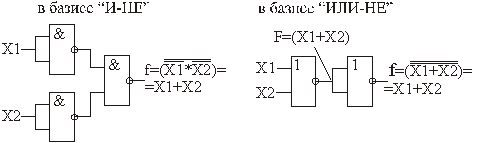
Реализация операции ИЛИ в базисе И-НЕ и ИЛИ-НЕ.

Пример реализации комбинационного устройства в базисе "И-НЕ". Пусть задана функция, реализуемая комбинационным устройством, в аналитической форме

F=x1x2+x3x4+x1x4

Используя закон де Моргана и с учетом закона двойного инвертирования, запишем эту функцию в виде

F = x1x2+x3x4+x1x4 = (x1x2)(x3x4)(x1x4)

 

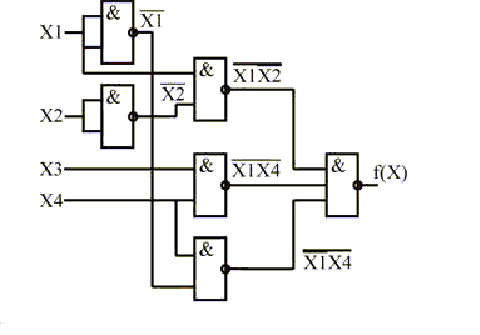
Как следует из полученного аналитического выражения, логическое устройство должно содержать три двухвходовых и один трехвходовой элемент И-НЕ. Функциональная схема комбинационного устройства, построенная в базисе И-НЕ, показана на рисунке.

                 

Мультиплексоры.

Во многих случаях возникает необходимость последовательного опроса логических состояний большого числа переменных и передачи их на один выход. Для этой цели служит специальное устройство, называемое мультиплексором.

Мультиплексор  передает сигнал с одного из информационных входов xi на единственный выход y, причем номер этого входа равен десятичному эквиваленту двоичного кода на адресных входах ai.

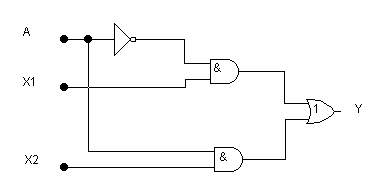
Создадим устройство, передающее на выход У один из двух входных сигналов Х1 или Х2 – мультиплексор 21.

Х 1

У

Х2

А

Таблица истинности устройства будет иметь вид:

Адресный вход	ВыходУ
0	Х1
1	Х2

Исходя из таблицы, построим ФАЛ: У = Х1*А + Х2*А.

Синтезируем устройство, соответствующее такой простой функции:

Х1 MUX

X2 Y

A

Условное графическое изображение мультиплексора.

На следуещем рисунке представлена схема мультиплексора на 4 входа.

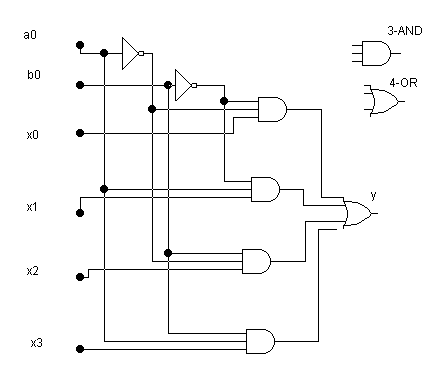
Мультиплексор имеет адресные входы а₀ и а₁ и 4 информационных входа х₀-х₃. В зависимости от состояния адресных входов выход мультиплексора соединяется с одним из его информационных входов. Схема построена таким образом, что с выходом соединяется тот вход, индекс которого равен двоичному числу, определяемому переменными а₀ и а₁. Непосредственно из схемы следует, что

y = a₁a₀x₀ + a₁a₀x₁ + a₁a₀x₂ + a₁a₀x₃

В формуле для у логическое произведение адресных сигналов равно единице только для той входной переменной, индекс которой совпадает с требуемым адресом. Например, если a₁ =1, а a₀=0, то

y = 1*1*x₀ + 1*0*x₁ + 0*1*x₂ + 0*0*x₃

По этому принципу эту схему можно распространить на любое число входных переменных. Если мультиплексор имеет n адресных входов, то ими можно коммутировать 2ⁿ информационных входов.

Промышленностью выпускаются следующие мультиплексоры в интегральном исполнении:

	TTL	ЭСЛ	КМОП
16 входов	SN 74150
8 входов	SN 74151	МС 10164	МС 14512
2х4 входа	SN 74153	МС 10174	МС14539
4х2 входа	SN 74157		МС14519

Кроме функции коммутации входов мультиплексор позволяет реализовать множество ФАЛ.

Пусть ФАЛ задана картой Карно:

x2x3
x1		00	01	11	10
	0	1	0	1	0
	1	0	1	0	1

Запишем ФАЛ

_ _ _ _ _ _

Y = x₁x₂x₃ + x₁x₂x₃ + x₁x₂x₃ + x₁x₂x₃

Сравним ее с формулой мультиплексора для 3-х переменных:

_ _ _ _ _ _ _ _ _ _ _

Y = A₀A₁A₂D₀ + A₀A₁A₂D₁ + A₀A₁A₂D₂ + A₀A₁A₂D₃ + A₀A₁A₂D₄ + A₀A₁A₂D₅ +

_

+ A₀A₁A₂D₆ + A₀A₁A₂D₇

Из сравнения получим значения коэффициентов D_i:

D₀ = D₃ = D₅ = D₆ = 1

D₁ = D₂ = D₄ = D₇ = 0

Тогда для реализации ФАЛ необходимо на адресные входы A_0, A_1, A₂ подать переменные x_{1 ,} x_{2 ,} x₃ а на информационные входы D₀ – D₇ подать 0 или 1 в соответствии с их значениями.

0 1

D₀

D₁ К8-1

D₂

D₃

D₄

D₅ Y

D₆

D₇

X₀ A₀

X₁ A₁

X₂ A₂

Мы рассмотрели простой случай, когда количество переменных равно количеству адресных входов.

Возможно построение ФАЛ на мультиплексоре даже если количество переменных превышает количество адресных входов.

В общем случае, когда требуется синтезировать КУ, реализующее функцию N аргументов на мультиплексоре с M управляющими входами и 2^М информационными входами, М младших переменных из набора Х₁, Х_2, . . . . Х_N следует подать на управляющие входы, а информационные сигналы (настроечные) D₀, D₁, . . . . D₂^м нужно представить функциями остальных (N - M) переменных, как показано на рис. Тогда синтез КУ сводится, по сути дела, к синтезу схемы формирования информационных сигналов, которую можно рассматривать как внутреннее более простое КУ.

X_m+1 D₀

К8-1

Схема

формиро-

вания

КУ Y

X_N

D₂^m

X₀ A₀

X_m A_m

Например, пусть требуется реализовать на мультиплексоре с 3-мя адресными входами (8 информационных) ФАЛ 4-х переменных:

Y = F(x4,x3,x2,x1)

Наведемо формулу комутатора з 3-ма адресними входами:

_ _ _ _ _ _ _ _

Y = А2А1А0D0 + А2А1А0D1 + А2А1А0D2 + А2А1А0D3 +

_ _ _ _

+ А2А1А0D4 + А2А1А0D5 + А2А1А0D6 + А2А1А0D7

Воспользуемся методом декомпозиции и представим ФАЛ в виде функции трех переменных x3,x2,x1 и функции на множестве: [0,1, четвертая переменная]. _ _ _ _ _ _ _

Y = f₀(0,0,0,x₄) x₁x₂x₃ + f₁(0,0,1,x₄) x₁x₂x₃ + f₂(0,1,0,x₄) x₁x₂x₃ +

_ _ _ _

f₃(0,1,1,x₄) x₁x₂x₃ + f₄(1,0,0,x₄) x₁x₂x₃ + f₅(1,0,1,x₄) x₁x₂x₃ +

_

f₆(1,1,0,x₄) x₁x₂x₃ + f₇(1,1,1,x₄) x₁x₂x₃

Подставляя значения аргументов, вычислим f_i.

Таким образом, для реализации заданной ФАЛ необходимо на 3 адресных входа А0, А1, А2 подать переменные x_1, x_2, x₃ , а на каждый из 8-ми информационных входов – соответствующее значение f_i.

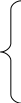
D₀

D₁ К8-1

0,1 D₂

Х4, D₃

Х4 D₄

D₅ Y

D₆

D₇

X₀ A₀

X₁ A₁

X₂ A₂

Заданную ФАЛ можно реализовать на 4-х входовых мультиплексорах.

Формула комутатора з двома адресними входами має вигляд:

_ _ _ _

Y = А1А0В0 + А1А0В1 + А1А0В2 + А1А0В3

Тоді після першої декомпозиції будемо мати:

_ _ _ _

F = f0(0,0)x2x1 + f1(0,1)x2x1 + f2(1,0)x2x1 + f3(1,1)x2x1

Для кожній f_i зробимо ще декомпозицію по х4,х3.

_ _ _ _

f0 = f₀₀(0,0)x4x3 +f₀₁(0,1)x4x3 + f₀₂(1,0)x4x3 +f₀₃(1,1)x4x3

_ _ _ _

f1 = f₁₀(0,0)x4x3 +f₁₁(0,1)x4x3 + f₁₂(1,0)x4x3 +f₁₃(1,1)x4x3

_ _ _ _

f2 = f₂₀(0,0)x4x3 +f₂₁(0,1)x4x3 + f₂₂(1,0)x4x3 +f₂₃(1,1)x4x3

_ _ _ _

f3 = f₃₀(0,0)x4x3 +f₃₁(0,1)x4x3 + f₃₂(1,0)x2x1 +f₃₃(1,1)x4x3

Підрахуємо f_ij:

f₀₀ = 0, f₀₁ = 0, f₀₂ = 1, f₀₃ = 0-;

f₁₀ = 1, f₁₁ = 0, f₁₂ = 1, f₁₃ = 0;

f₂₀ = 0, f₂₁ = 0, f₂₂ = 1, f₂₃ = 1;

f₃₀ = 1, f₃₁ = 0, f₃₂ = 0, f₃₃ = 1;

Отже кожна функція f_i буде реалізуватися на окремому комутаторі, а виходи кожного з них треба подати ра інформаційні входе ще одного комутатора.

0 1 X4 X3 X2 X1

Счетчики.

Электронные счетчики ( далее, просто счетчики) позволяют вести подсчет электрических импульсов, количество которых (поступивших на вход счетчика) представляется, обычно, в параллельном коде. Счетчики могут отличаться модулем счета и типом счетной последовательности, которая, в частности, может быть двоичной, двоично-десятичной, в коде Грея и т.п. Цифровые последовательностные устройства, выполненные по схеме счетчика, но имеющие один счетный вход и один выход называются делителями частоты. Таким образом, любой счетчик может служить в качестве делителя частоты, если используется информация только одного из его выходов. Так как счетчики и делители имеют единую структуру, основное внимание будет уделено синтезу счетчиков.

Счетчики и делители подразделяются на асинхронные и синхронные. У синхронных счетчиков все разрядные триггеры синхронизируются параллельно одними и теми же синхроимпульсами, поступающими из источника этих импульсов. Асинхронные счетчики имеют последовательную синхронизацию, т.е. каждый последующий разрядный триггер синхронизируется выходными импульсами триггера предыдущего разряда. Асинхронные счетчики иногда называют последовательными, а синхронные счетчики - параллельными.

Синхронные счетчики, в свою очередь, подразделяются на параллельно-синхронные и последовательно-синхронные. Параллельные счетчики имеют более высокую скорость счета, чем асинхронные.

Счетчики, независимо от способа синхронизации, подразделяются на счетчики прямого счета (суммирующие) и на счетчики обратного счета (вычитающие). В интегральном исполнении выпускаются также реверсивные счетчики, в которых имеется специальный вход для переключения режима работы, т.е. направления счета. Многие типы счетчиков, выпускаемые промышленностью в интегральном исполнении, имеют дополнительные входы предустановки, позволяющие использовать эти счетчики в режиме регистра памяти.

В качестве разрядных триггеров счетчиков и делителей могут быть использованы двухступенчатые D-триггеры, Т- и JK-триггеры.

Счетчики относятся к последовательностным устройствам с циклически повторяющейся последовательностью состояний. Число, соответствующее количеству импульсов (поступивших на вход счетчика), при котором счетчик “возвращается” в исходное состояние, называется модулем или коэффициентом счета. Модуль счета, обычно, обозначают буквой М (или К_сч). Например, максимальный модуль счета счетчика из двух триггеров равен М = 2² = 4, трех триггеров - М = 2³ = 8 и т.д. В общем случае для n - разрядного счетчика - М = 2ⁿ. Модуль счета счетчика численно совпадает с модулем деления делителя частоты. Счетчик по модулю 8 позволяет реализовать (без дополнительных схемных затрат) делитель частоты на 8. Это значит, что данный делитель делит частоту входной импульсной последовательности на 8.

Счетчики с произвольным коэффициентом счета. Принцип построения подобного класса счетных устройств состоит в исключении нескольких состояний обычного двоичного счетчика, являющихся избыточными для счетчиков с коэффициентом пересчета, отличающимися от двоичных. При этом избыточные состояния исключаются с помощью обратных связей внутри счетчика.

Число избыточных состояний для любого счетчика определяется из следующего выражения:

М = 2^m - К_сч,

где М - число запрещенных состояний, К_сч - требуемый коэффициент счета; 2^m - число устойчивых состояний двоичного счетчика.

Задача синтеза счетчика с произвольным коэффициентом счета заключается в определении необходимых обратных связей и минимизации их числа. Требуемое количество триггеров определяется из выражения

n= [log₂ К_сч],

 

где [log₂ К_сч] - двоичный логарифм заданного коэффициента пересчета К_сч, округленный до ближайшего целого числа.

В каждом отдельном случае приходится применять какие-то конкретные методы получения требуемого коэффициента пересчета. Существует несколько методов получения счетчиков с заданным коэффициентом пересчета К_сч.

Один их этих методов заключается в немедленном сбросе в “0” счетчика, установившегося в комбинацию, соответствующему числу К_сч. Его называют также методом автосброса. Рассмотрим пример реализации счетчика с К_сч=10 методом автосброса. Очевидно, что “сбрасывая” двоичный четырехразрядный счетчик на нуль каждый раз, когда он будет принимать состояние 1010, можно обеспечить”возврат” счетчика в исходное состояние после каждых десяти импульсов.

Другой метод проектирования счетчиков с заданным коэффициентом счета заключается в построении таблицы переходов, в первых столбцах которых будут отражены текущие состояния триггеров счетчика, а в последующих - следующие за ними состояния. Анализ таблицы позволяет установить те переходы, которые должны быть “сделаны” триггерами, входящими в состав счетчика. Затем с помощью управляющей таблицы соответствующего триггера находятся значения логических функций на управляющих входах триггеров, позволяющие осуществить эти переходы.

Синтезируем для примера счетчик-делитель на 6 на основе D-триггеров.

По формуле определим количество триггеров – 3. Построим таблицу переходов. Считая состояние 000 первым, состояния 1- 5 будут рабочими. 6-е состояние соответствует сбросу в начало счета. Последующие состояния обозначим .

№	Q3	Q2	Q1	Q3N+1	Q2N+1	Q1N+1	F
1	0	0	0	0	0	1	0
2	0	0	1	0	1	0	0
3	0	1	0	0	1	1	0
4	0	1	1	1	0	0	0
5	1	0	0	1	0	1	0
6	1	0	1	0	0	0	1
7	1	1	0				
8	1	1	1				

Для каждого выхода триггера Q_i составим карту Карно и получим соответствующую ФАЛ.

X2X1
	Q1N+1				Q2N+1				Q3N+1
	00	01	11	10	00	01	11	10	00	01	11	10
X3 0 1	1			1		1		1			1
	1	0			0	0			1	0		

_ _ _ _ _

Q1 = X1; 2 = X3X2X1 + X2X1; D3 = X2X1 + X3X1

С учетом формулы D-триггера при входе С=1, получим

_ _ _ _ _

D1 = X1; D2 = X3X2X1 + X2X1; D3 = X2X1 + X3X1

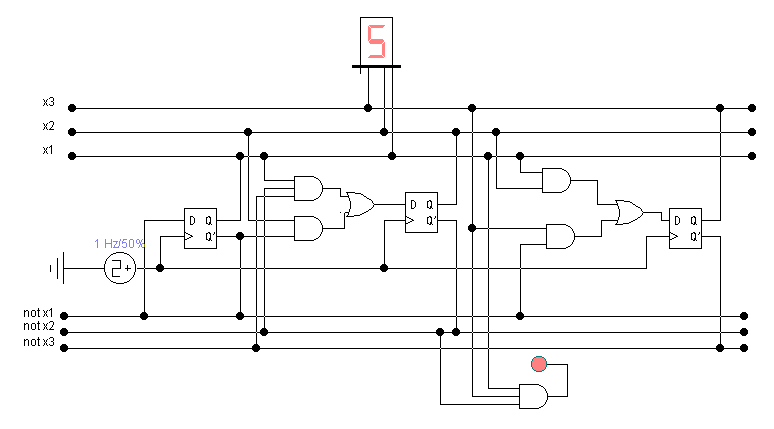
Разработанный счетчик до 6 осталось добавить индикатором каждого 6-го импульса. Его формулу получим из 6-той строки таблицы переходов.

_

F = Q1Q2Q3.