Введение

Лабораторный практикум является обязательной составляющей изучения курса физики на естественных факультетах. В течение каждого семестра изучения физики студенты должны выполнить лабораторные работы, тематика и количество которых определены учебной программой курса для данного направления.

Цели лабораторного физического практикума:

1. Изучение основ физики с использованием экспериментальных методов.

2. Знакомство с методикой проведения физического эксперимента.

3. Приобретение опыта проведения измерений физических величин и оценки их погрешностей.

Для успешного выполнения лабораторной работы и получения зачета за отведенное время студент обязан заранее подготовится к занятию и составить конспект лабораторной работы в соответствии с требованиями методических указаний. Если в течение аудиторного занятия студент не успел получить зачет по лабораторной работе, он должен провести необходимую обработку результатов измерений во внеучебное время, правильно оформить работу и представить ее для получения зачета на следующем по расписанию лабораторном занятии.

Организация учебного процесса в лабораториях осуществляется в соответствии с утвержденными на кафедре общей физики нормами и правилами проведения лабораторных работ, с которыми студенты знакомятся на первом занятии.

Этапы выполнения лабораторной работы:

1. получение допуска к лабораторной работе;

2. правильное и самостоятельное проведение измерений;

3. обработка результатов измерений;

4. получение зачета по лабораторной работе.

Подготовка к допуску осуществляется с использованием методических указаний к лабораторной работе и рекомендованной литературы. Проводится оформление раздела «Краткая теория» в конспекте лабораторной работы.

Допуск студентов к лабораторной работе преподаватель проводит в виде собеседования со студентом. Подготовка к получению допуска к лабораторной работе является основой для ее правильного, грамотного и наиболее быстрого выполнения. В течение подготовки к допуску, которую необходимо проводить заранее во внеучебное время, студент должен выполнить следующее:

1. Подготовить конспект лабораторной работы по установленной форме.

2. Изучить основы теории физического явления, исследуемого в лабораторной работе, и запомнить формулировки понятий, используемых в теории.

3. Разобраться с выводом основных формул, которые используются в лабораторной работе. Понять вид функций и графиков, которые должны быть получены в работе, а также значения или оценки рассчитываемых величин.

4. Понять процедуру проведения измерений и последовательность обработки результатов измерения.

После получения допуска каждый студент самостоятельно проводит обработку результатов измерения и их представление в соответствии с методическими рекомендациями к лабораторной работе.

Итогом работы служит предоставление оформленного отчета по лабораторной работе и получение зачета у преподавателя.

Лабораторная работа № 315

Определение момента инерции тел правильной формы методом крутильных колебаний

Оборудование: тренога со спиральной пружиной, штанга с двумя грузами, секундомер, световой барьер.

Цель работы: определение момента инерции тел правильной формы.

Краткая теория

Момент инерции тела относительно неподвижной оси - физическая величина, равная сумме произведений элементарных масс на квадраты их расстояний до рассматриваемой оси и являющаяся мерой инертности тела во вращательном движении

.

С уммирование производится по всем элементарным массам _, на которые можно разбить тело.

Рисунок 1 – Разбиение тела на элементарные массы

Момент инерции — величина аддитивная: момент инерции тела равен сумме моментов инерции его частей.

Момент инерции тела в случае непрерывного распределения масс

_,

где ρ - плотность тела в данной точке; dm=ρdV - масса малого элемента тела объемом dV, отстоящего относительно оси вращения на расстоянии r.

Интегралы берутся по всему объему тела, причем величины ρ и r являются функциями точки (например, декартовых координат х_, у и z).

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела I относительно любой оси вращения равен моменту его инерции I_c относительно параллельной оси, проходящей через центр масс тела, сложенному с произведением массы m тела на квадрат расстояния а между осями.

.

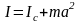Момент силы относительно неподвижной точки - физическая величина, определяемая векторным произведением радиуса-вектора , проведенного из точки в точку приложения силы, на силу

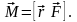
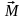- осевой вектор (псевдовектор), его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Модуль вектора момента силы

где - угол между и , 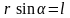- кратчайшее расстояние между линией действия силы и точкой - плечо силы.

Р исунок 2 – Момент силы относительно неподвижной очки О

М омент силы относительно неподвижной оси - скалярная величина , равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки данной оси .

Рисунок 3 – Момент силы относительно неподвижной оси

_{Значение момента} не зависит от выбора положения точки на оси . Если ось _{совпадает с направлением вектора , то момент силы представляется в виде вектора, совпадающего с осью:}

_.

Момент импульса материальной точки относительно неподвижной точки - физическая величина, определяемая векторным произведением радиуса-вектора материальной точки, проведенного из точки , на импульс этой материальной точки

Модуль вектора момента импульса

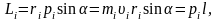
где α – угол между векторами и ; 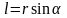- плечо импульса. Перпендикуляр опущен из точки на прямую, вдоль которой направлен импульс частицы.

Р исунок 4 – Момент импульса материальной точки относительно неподвижной точки О

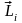- осевой вектор (псевдовектор), его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Момент импульса материальной точки относительно неподвижной оси z - скалярная величина L_iz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки данной оси z.

Значение момента импульса L_iz не зависит от положения точки О на оси z.

Р исунок 5 – Момент импульса материальной точки относительно неподвижной оси z

Момент импульса отдельной точки вращающегося абсолютно твердого тела

.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса с некоторой скоростью . Скорость и импульс перпендикулярны этому радиусу, т. е. радиус — плечо вектора . Тогда момент импульса отдельной частицы и направлен по оси в сторону, определяемую правилом правого винта.

Момент импульса абсолютно твердого тела относительно неподвижной оси z - сумма моментов импульса отдельных его частиц относительно той же оси

,

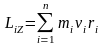равен произведению момента инерции тела относительно той же оси на угловую скорость

_.

_{Учтем, что}

,

где 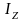- момент инерции тела относительно оси z, – угловая скорость.

Найдем выражение для работы при вращении тела (Рисунок 6). Сила приложена к точке , находящейся от оси на расстоянии 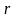, - угол между направлением силы и радиусом-вектором . Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.

При повороте тела на бесконечно малый угол точка приложения силы проходит путь и работа равна произведению проекции силы на направление смещения на величину смещения: . Учитывая, что 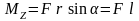, получаем

Рисунок 6 – К вычислению работы при вращении тела

Работа вращения тела идет на увеличение его кинетической энергии: , , . Тогда , или . Так как угловая скорость , то .

Уравнение динамики вращательного движения твердого тела:

.

Момент сил твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловое ускорение.