І МОДУЛЬ. СЫЗЫҚТЫ АЛГЕБРА ЖӘНЕ

АНАЛИТИКАЛЫҚ ГЕОМЕТРИЯ

БІРІНШІ ЛЕКЦИЯ

МАТРИЦА. НЕГІЗГІ ҰҒЫМДАР

Анықтама. m жатық n тік жолдан құрылған кестені mxn өлшемді матрица деп атайды.

Матрицаны құрайтын сандар матрица элементтері деп аталады. Әдетте матрица латын алфавитінің бас әріптерімен, ал элементтері сәйкес кіші әріптермен белгіленеді:

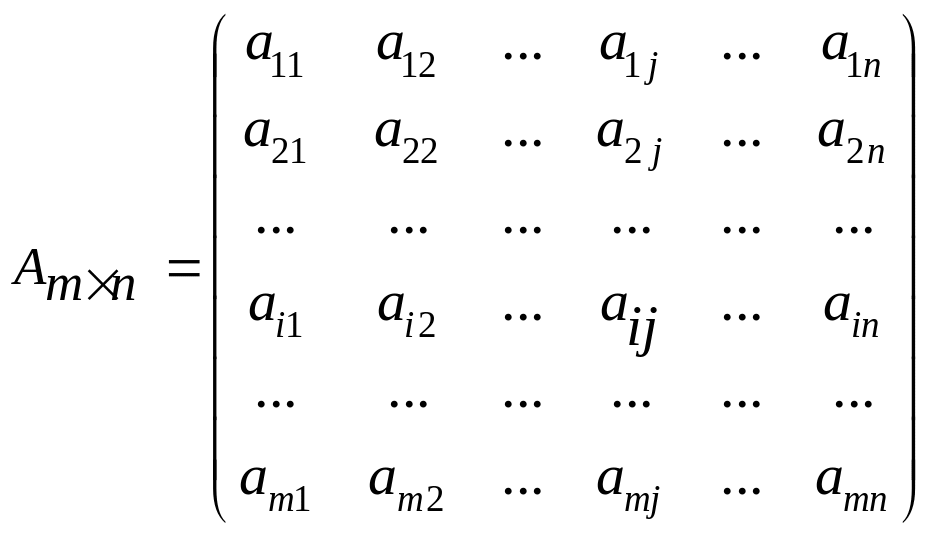
Қысқаша жазылуы:

Матрица элементінің бірінші индексі жатық жол нөмірі, ал екінші индексі тік жол (бағана) нөмірін көрсетеді. Мысалы, элементі екінші жатық жол мен үшінші тік жол қиылысында орналасқан.

Бір ғана жатық жолдан құралған матрицаны жол-матрица, ал бір ғана тік жолдан құралған матрицаны бағана-матрица деп атайды:

- жол-матрица;

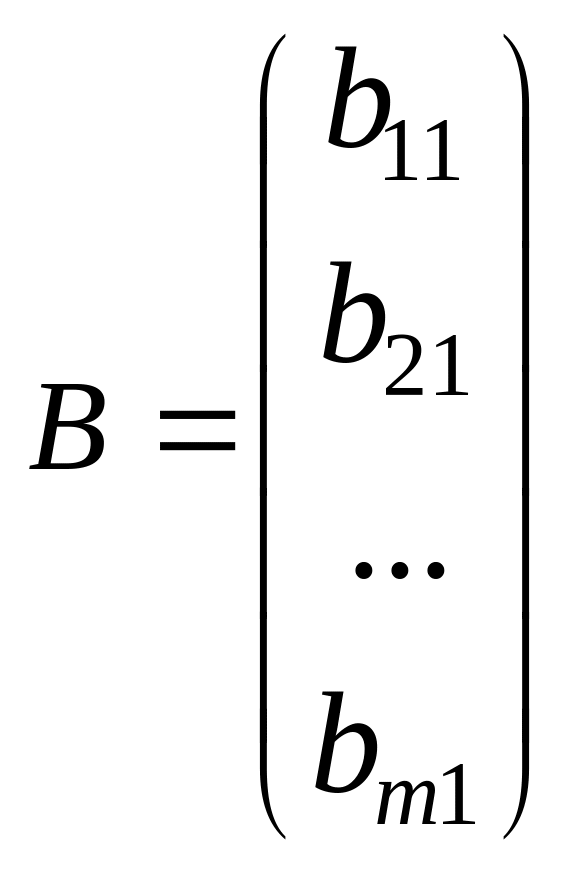- бағана матрица.

Жол матрица мен бағана матрицаны кейде вектор деп те айтады..

Жатық жолдар саны мен тік жолдар саны тең болатын матрица квадрат матрица деп аталады,

.

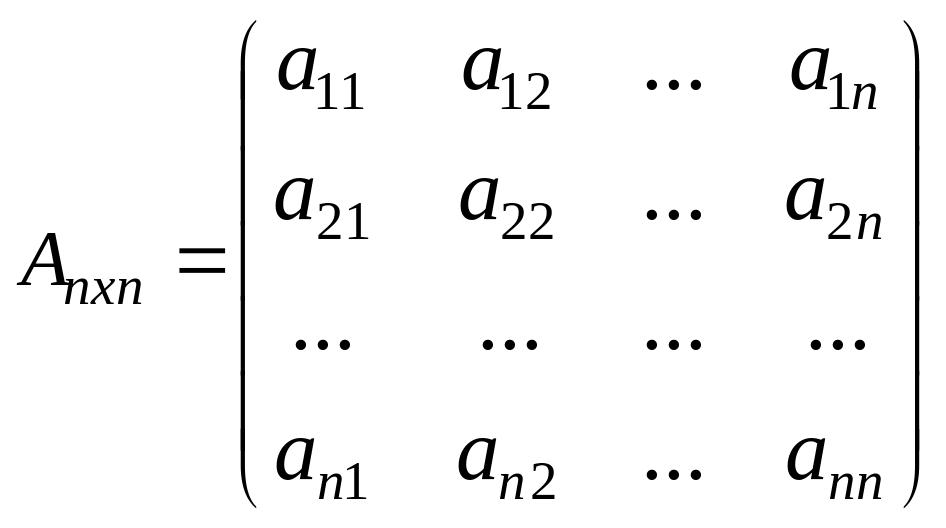Квадрат матрицаның элементтері диагоналдық элементтер деп аталады да, матрицаның негізгі диагоналін құрайды. Ал элементтері қосымша диагоналдық элементтер деп аталады да, матрицаның қосымша диагоналін құрайды.

Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,

,

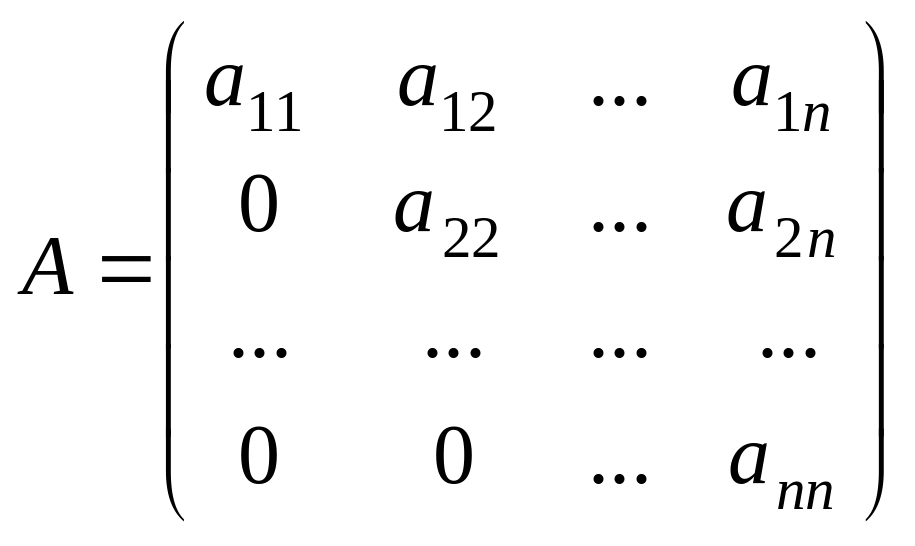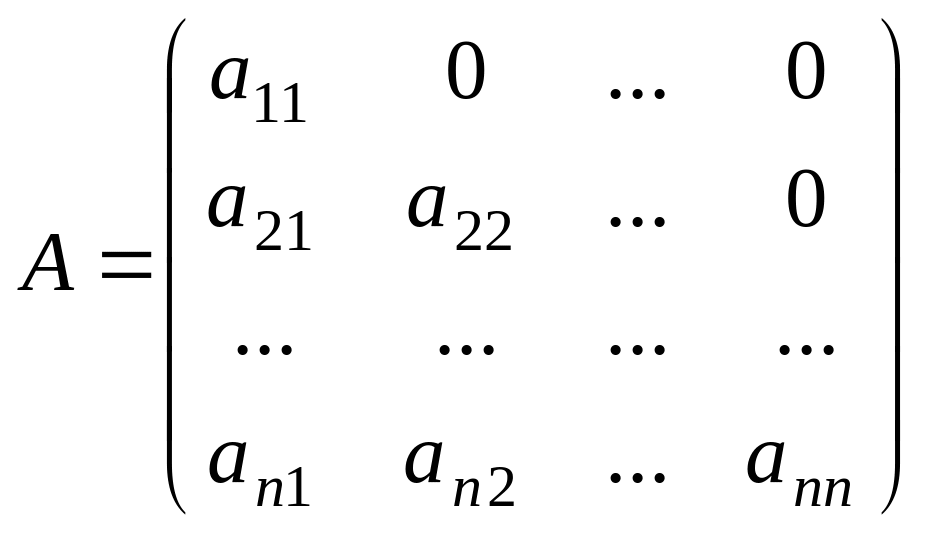
Диагоналды емес элементтерінің бәрі нолге тең болатын квадрат матрица диагоналды матрица деп аталады,

.

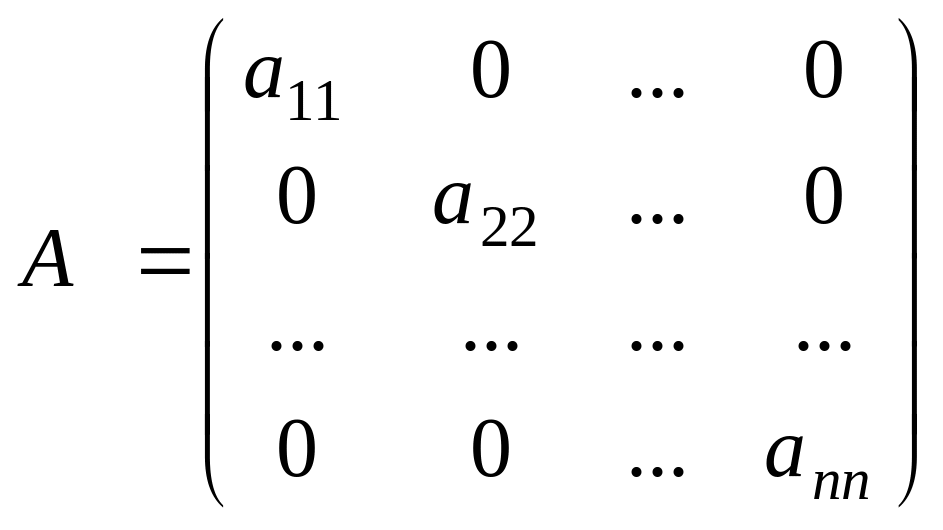Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,

.

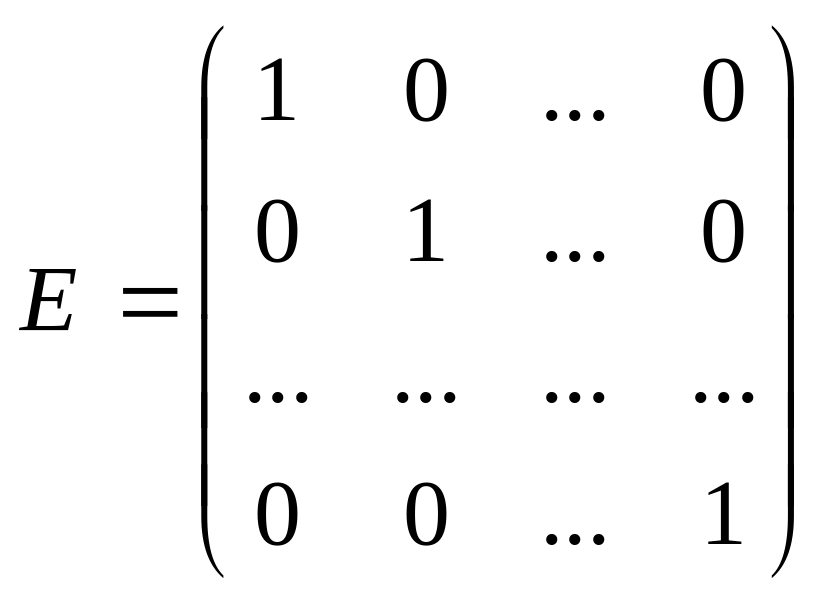Барлық элементтері нолге тең матрица нолдік матрица деп аталады.

Матрицаларға қолданылатын амалдар

1. Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:

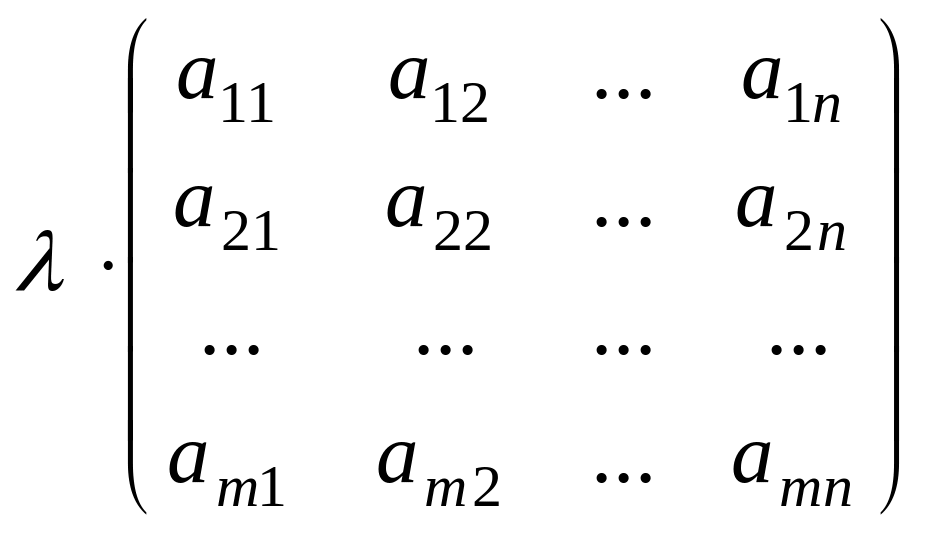
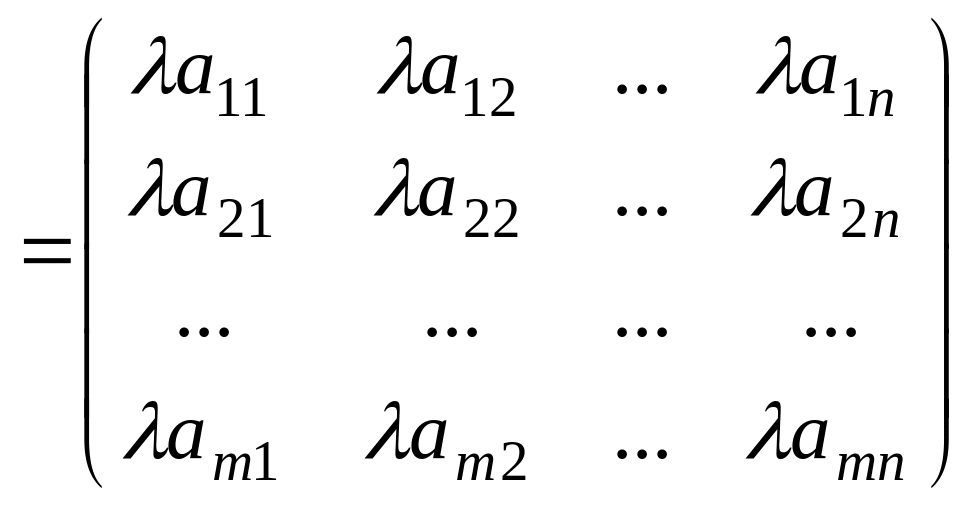
Мысалы, матрицасын санына көбейтейік:

.

Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.

2. Матрицаларды қосу және алу. Өлшемдері бірдей матрицаларды ғана қосуға болады. 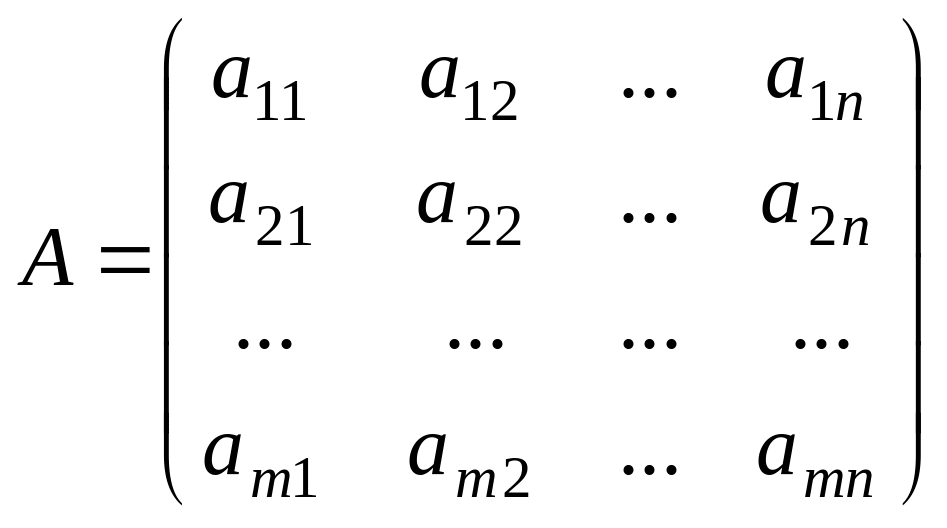және 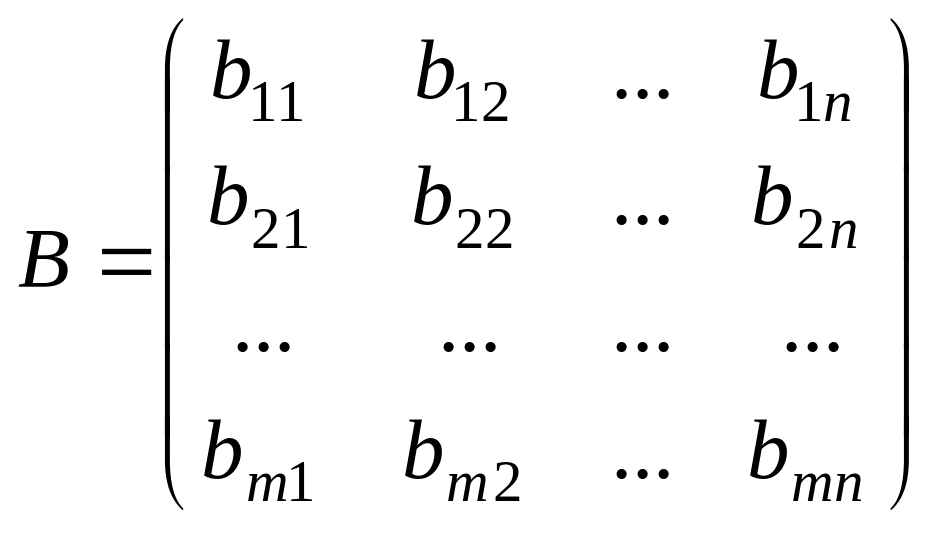матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз:

.

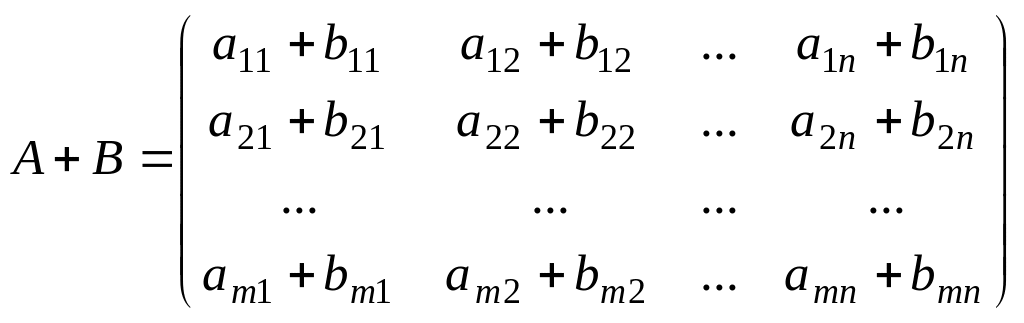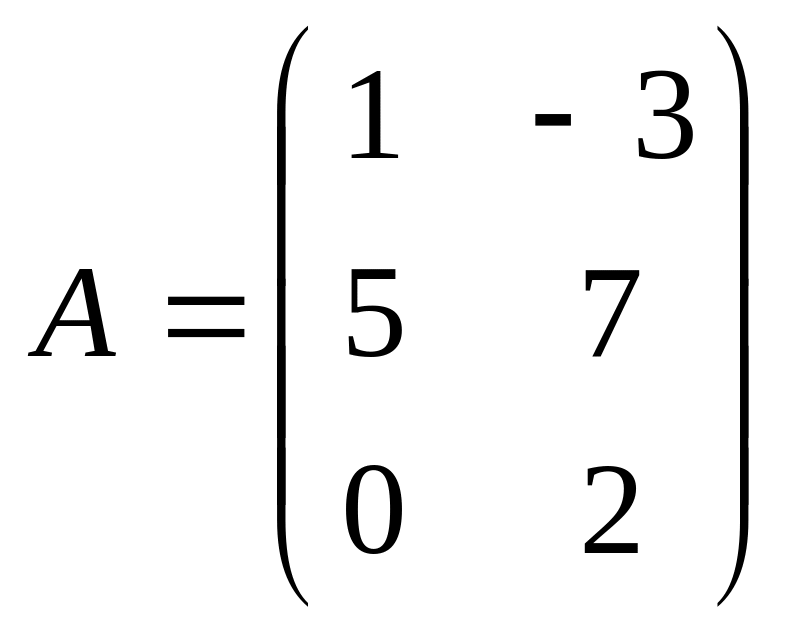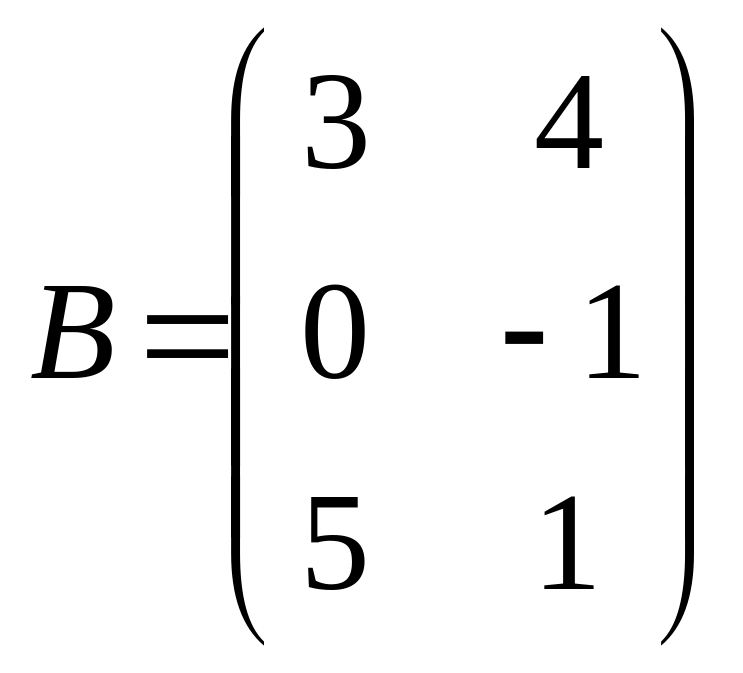Мысалы, мен матрицаларын қосайық:

.

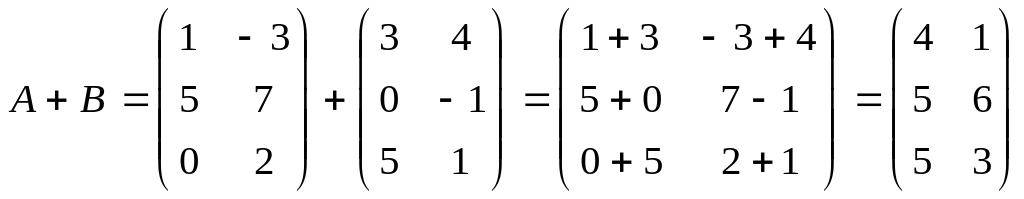А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті:

A – B = A+(-1)B

немесе А матрицасының әр элементінен В матрицасының сәйкес элементтері алынады. Мысалы А матрицасынан В матрицасын алайық:

.

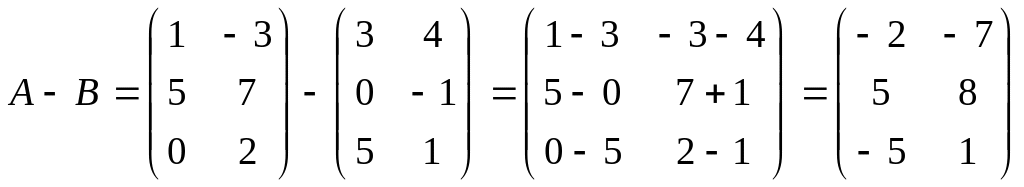3. Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі mxk болатын А матрицасы мен өлшемі kxn болатын В матриасы берілсін:

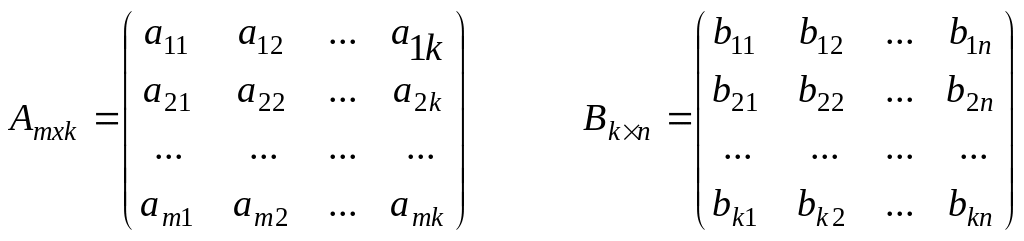
Осы екі матрицаны көбейткенде өлшемі mxn болатын көбейтінді С матрица аламыз:

С матрицасының элементі А матрицаның –жатық жол элементтерін В матрицаның –тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады:

, . (1)

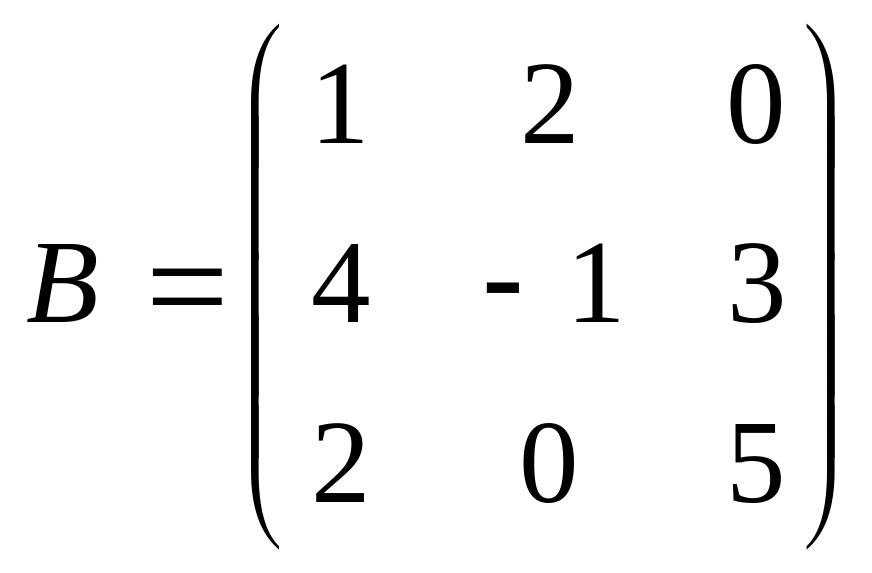Мысалы, матрицасы мен матрицасын көбейтейік. Бірінші матрица үш тік жолдан, ал екінші матрица үш жатық жолдан тұрғандықтан бұл матрицаларды көбейтуге болады. Көбейтінді матрицаның өлшемін анықтайық:

,

яғни, . k=3 болғандықтан (1) формуланы қолданғанда үш қосылғыш болады:

, .

элементін табу үшін формуладағы i=1, j=1 деп аламыз, сонда

,

яғни А матрицаның 1-жатық жол элементтерін В матрицаның 1-тік жолының сәйкес элементтеріне көбейтіп қостық. Осылай С матрицаның барлық элементтері табылады:

C= = = = .

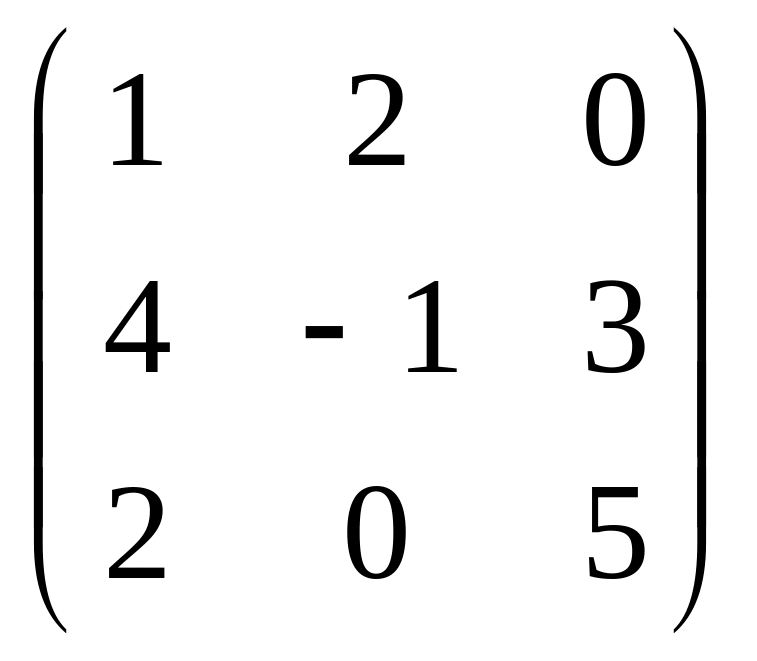Қосу және көбейту амалдарының мынадай қасиеттері бар:

1) A+B=B+A	5) (A+B)C=AC+BC
2) (A+B)+C=A+(B+C)	6) (AB)=( A)B=A( B)
3) (A+B)= A+ B	7) A(BC)=(AB)C
4) A(B+C)=AB+AC

Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық.

8) Біріншіден, екі матрицаның АВ көбейтіндісі болғанмен ВА көбейтіндісі болмауы мүмкін. Мысалы, көбейтіндісі бар, бірақ көбейтіндісі жоқ, себебі бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең емес;

екіншіден, АВ және ВА көбейтінділері бар болғанмен, олардың өлшемдері әртүрлі болуы мүмкін. Мысалы, және көбейтінділер бар, бірақ өлшемдері әртүрлі:

, ;

үшіншіден, АВ және ВА көбетінділер бар және олардың өлшемдері бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті заңы орындалмайды, яғни АВ BA.

Мысал. мен матрицалары берілген. АВ және ВА көбейтінділерін табау керек.

Шешуі. Берілген матрицалар өлшемдері 2х2 квадрат матрицалар, оларды көбейтуге болады:

.

.

Көріп отырғанымыздай АВ BA.

9) А-квадрат матрица болса, онда мына теңдік орындалады:

АЕ = ЕА = А.

4. Матрицаны транспонерлеу. Қандай да бір А матрицасының жатық жолын сәйкес тік жол етіп жазғаннан пайда болған матрицаны берілген матрицаның транспонерленген матрицасы деп атайды да, деп белгілейді. Берілген матрицаның өлшемі mxn болса, оның транспонерленген матрицасының өлшемі nxm болады. Мысалы, матрицасының бірінші жатық жолын бірінші тік жол етіп, ал екінші жатық жолын екінші тік жол етіп жазып оның транспонерленген матрицасын 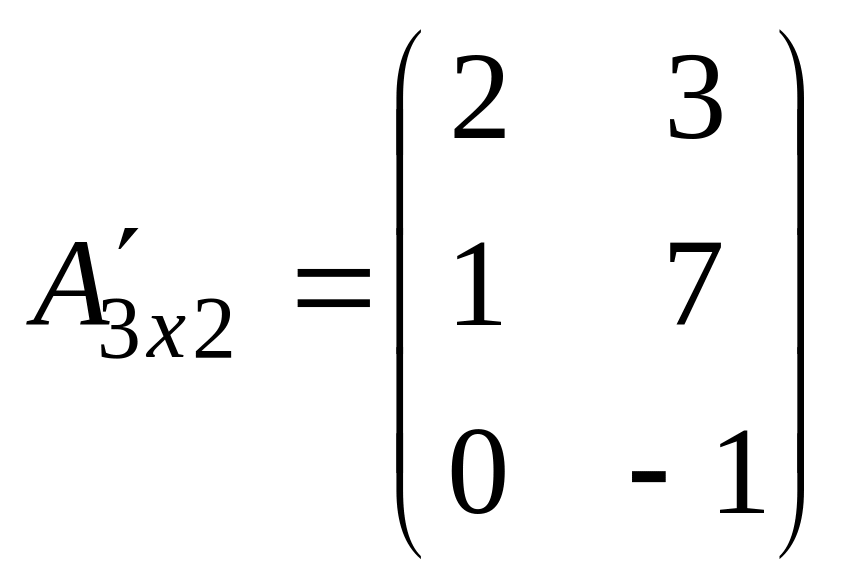аламыз.