Ответы на экзаменационные вопросы по физике / 8

Теория атома водорода по Бору

В качестве последнего примера безуспешных попыток классической физики дать полную теорию физических явлений рассмотрим атом водорода.

Согласно классической модели Резерфорда атом водорода состоит из одного электрона, вращающегося вокруг положительно заряженного малого атомного ядра. Эта классическая модель не смогла объяснить два основных экспериментальных факта:

а) стабильность атома водорода

б) структуру излучаемого им электромагнитного спектра.

В основу теории, исходящей из ядерной модели атома и объясняющей его основные опытные свойства и, прежде всего устойчивость и дискретный спектр излучения, Н. Бор положил два постулата (принципа):

1. Постулат стационарных состояний¹ (орбит) – в атоме существуют некоторые особые стационарные состояния, находясь в которых электрон вращается вокруг ядра по круговым орбитам и не излучает, хотя и движется с ускорением (центростремительным). Этим постулатом Бор, не покушаясь на справедливость теоретических основ классической физики, допускает исключение из общего правила в виде особых состояний атома с круговыми орбитами электрона в них.

Бор установил (догадкой) правило определения стационарных круговых орбит электрона – так называемое правило квантования орбит. Оно утверждает необходимость целочисленности в постоянных Планка момента импульса L электрона на этих орбитах, т. е.: L = mr = n, где m и  – масса и скорость электрона, r – радиус его орбиты, n – номер орбиты; - постоянная Планка.

Правило частот. Излучение и поглощение энергии атомом происходит при переходе его из одного стационарного состояния в другое (при переходе электрона с одной стационарной орбиты на другую²). Частота излучения (поглощения) определяется из условия энергетического баланса: , где и - энергии электрона на m - ой и n - ой орбитах, соответственно.

Процесс обратный излучению заключается в поглощении фотона с частотой _nm. В этом случае атом переходит из состояния с меньшей энергией в состояние с большей энергией.

Д

искретность, квантованность энергетических уровней электрона в атоме (и атома в целом), гипотетически постулируемая Бором, получила свое убедительное экспериментальное подтверждение в опыте Франка и Герца в 1913 г. Пропуская электрический ток через лампу - триод, наполненную парами ртути, они обнаружили провалы на вольтамперной характеристике I(U). Эти провалы, т. е. снижения силы тока при некоторых значениях напряжения между анодом А и сеткой С, были объяснены ими как результат неупругого соударения носителей тока – электронов с атомами ртути³. Сетка С, на которую подавался небольшой, порядка 0,5 В положительный потенциал относительно анода, «перехватывала» «ослабевшие» электроны, потерявшие свою кинетическую энергию в результате неупругих соударений с атомами ртути. Соответственно на анод попадало меньше электронов, что проявляло себя в уменьшении анодного тока. Атомы ртути могли воспринять (забрать) от электронов лишь определенную энергию, кратную энергии их возбуждения. При этом атомы ртути переходят в возбужденные состояния, отстоящие от основного по энергии на 4,9 эВ; 6,7 эВ; 10,3 эВ… . Это говорит о том, что энергия атома ртути обладает дискретным спектром значений.

В математическом плане Бор при построении теории простейшего атома – атома водорода, отталкивался от двух уравнений для электрона в атоме. Одно из них было чисто классическим, представляя собой, второй закон Ньютона с кулоновской силой (центростремительной), а другое – чисто квантовым – уравнение для момента импульса электрона (правило квантования орбит). Отсюда следовал вывод о непоследовательности теории Бора, которая была уже не чисто классической, но не была еще и последовательно квантовой. Такая непоследовательность обусловила значительную ограниченность теории Бора, ее предсказательных возможностей.

Запишем и решим систему из двух уравнений для электрона в атоме с порядковым номером Z. Напомним, что у Бора Z = 1, что соответствовало атому водорода.

здесь ; ; ;

n = 1, 2, 3, … - номера орбит.

Имеем систему двух уравнений с двумя неизвестными  и r. Избавимся от , возведя второе уравнение в квадрат и поделив его на первое, в котором сократим r:

 = .

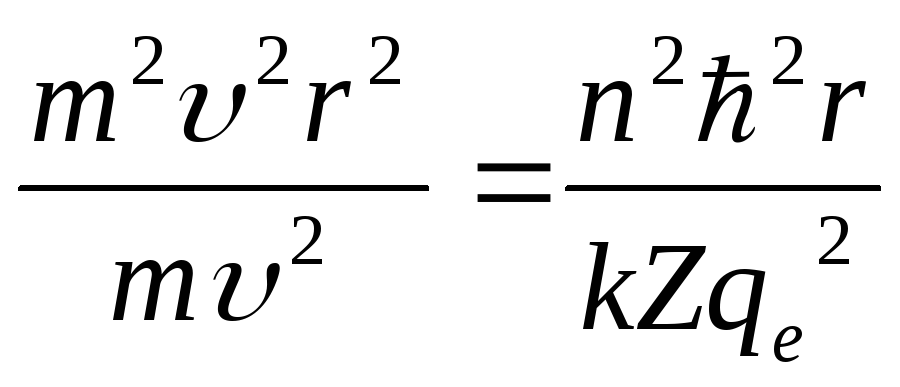
П

олученное выражение для радиуса орбиты электрона в атоме указывает на дискретный, квантовый характер его значений. Для n = 1 и Z = 1 значение радиуса первой (невозбужденной) орбиты r₁ = 0,5310^-10 м - хорошо совпадает с размером атома водорода.

Скорость электрона также квантуется:

, причем _n  1/n.

Полная энергия электрона в атоме складывается из суммы кинетической и потенциальной: ;

- энергия взаимодействия двух, разных по знаку, точечных зарядов – электрона и ядра.

Для   с: ;

Полученное выражение для полной энергии электрона в атоме содержит набор отрицательных значений; это является свидетельством связанности состояния электрона в атоме – энергия связи (отрицательная) превышает энергию движения (положительную). При возрастании полной энергии до нуля электрон оказывается свободным, а атом ионизированным.

С

ростом номера и радиуса орбиты полная энергия электрона возрастает, оставаясь до уровня ионизации отрицательной. При n   и  E = 0 – электрон отрывается от ядра, а атом превращается в положительный ион.

Подставляя в выражение для полной энергии электрона ранее выражение для радиуса его орбиты, получаем формулу для полной энергии электрона: . Полная энергия Е электрона в атоме квантуется, т. е. имеет дискретный спектр.

Для n = 1 (атом водорода)  -13,6 эВ; ; ; … Е_ = 0.

Энергетические уровни атома с ростом номера уровня сгущаются, и при n   изменение энергии атома происходит почти непрерывно. Имеем переход к классической физике, выражаемый принципом соответствия⁴ Бора.

Разность энергий электрона на втором и первом энергетических уровнях называется энергией возбуждения атома: Е_в = Е₂ – Е₁. Энергии возбуждения соответствует потенциал возбуждения V_в: Е = q_еV_в. Для водорода Е_в = 10,2 эВ и V_в = 10,2 В.

Разность энергий на бесконечно удаленной от ядра и первой орбитах называется энергией ионизации, т. е. отрыва электрона от атома; для водорода Е_ = Е_ – Е₁ = - Е₁ = 13,6 эВ.

Энергия фотона, излучаемого при переходе электрона с m - ой на n - ую орбиты может быть записана в виде: Е = Е_(1/n² – 1/m²).

Объяснение закономерностей линейчатого спектра атома водорода.

Вытекающая из теории Бора дискретная структура энергетических уровней электрона в атоме позволяет объяснить закономерности в спектре излучения атома водорода. Из опыта известно, что спектр теплового излучения невзаимодействующих атомов имеет дискретный характер в виде совокупности отдельных спектральных линий, которые определенным образом упорядочены в некоторые группы, называемые сериями. Такая сериальная упорядоченность спектра излучения атома водорода описывается обобщенной формулой Бальмера:

, где и - постоянные Ридберга: ,

n - номер спектральной серии; n = 1, 2, 3 …

m - номер спектральной линии в серии; m = n + 1, m + 2 …

При n = 1;  =(1 – 1/m²), где m = 2, 3, 4 … - серия Лаймана – лежит в ультрафиолетовом диапазоне.

n = 2;  =(1/2² – 1/m²), где m = 3, 4, 5… - серия Бальмера – первые четыре ее линии лежат в

видимой области спектра.

n

= 3;  =(1/3² – 1/m²), где m = 4, 5, 6 … - серия Пашена – лежит в инфракрасной области.

Наглядное представление механизма образования сериально упорядоченного линейчатого спектра атома водорода дано на схеме.

Теория Бора позволяет просто получить и саму обобщенную формулу Бальмера. Выразим из правила частот Бора частоту  излучения:

и, подставив в нее выражение для энергии: получим:

Сравнивая с формулой Бальмера, видим, что постоянная Ридберга образуется набором фундаментальных физических констант: при Z = 1. Подставляя их значения, получим для значение , совпадающее с известным из опыта.

Формулу Бальмера часто записывают не для частоты , а для обратной длины волны 1/.

Из  = с/  1/ = /с = (/с)(1/n² – 1/m²) = R(1/n² – 1/m²), где R = /с = .

Спектральная линия с наибольшей длиной волны в данной серии называется ее головной линией, а с наименьшей длиной волны – границей серии.

Формула Бальмера оказывается применимой для так называемых водородоподобных атомов. К ним относят ионизованные атомы, имеющие один электрон, например, однократно ионизованный атом гелия Не⁺ ( = 2) и двухкратно ионизованный атом лития L⁺⁺ ( = 3).

Ограниченность теории Бора.

Теория Бора была первым серьезным шагом на пути внедрения квантовых идей в физику вещественного состояния материи. Она позволила вывести характер спектра излучения простейшего атома – водорода, но была не в состоянии предсказать распределение интенсивностей в этом спектре, а также рассчитать спектр более сложных, чем водород атомов. Такая ограниченность теории Бора объяснялась ей внутренней непоследовательностью, паллиативностью (половинчатостью). Здесь был сделан лишь один, первый “квантовый шаг”, который вскрыл плодотворность квантовой гипотезы и необходимость ее более полного воплощения в теории. Оно было последовательно осуществлено в рамках новой фундаментальной физической теории – квантовой механики.

В квантовой механике был найден такой формально - математический аппарат, из которого квантованность (дискретный спектр) мер движения частицы получалась как следствие определенных условий движения и взаимодействия, а не вводилась “вручную”, постулативно, как это вначале было осуществлено Н. Бором.

1 Стационарное состояние с наименьшей энергией называется основным.

2 Возможны переходы электрона в атоме «сверху вниз» и без излучения кванта света. В этом случае энергия возбуждения отдается обычно решетке твердого тела, то есть в виде внутренней, тепловой энергии.

3 Обычно соударения легкого электрона с массивным атомом ртути носят упругий характер – без изменения энергии электрона.

4 В квантовой механике принцип соответствия будет выражаться иным, нежели n   условием, а именно  0.