Розв’язок.

а) Область визначення функції знайдемо з умови , отже ; .

Значить .

область значень .

б) Щоб знайти точки перетину графіка з осями координат, покладемо:

, отже ;

, отже при .

Значить, точка перетину графіка з віссю OX має координати , а з віссю OY - .

в) Як видно, область визначення функції - симетрична відносно початку системи координат, точки , а тому разом з будь-яким аргументом їй належить і протилежний - .

Перевіримо, чи виконується одна з рівностей: , що визначає парну функцію, або , що визначає непарну функцію.

, отже функція не є ні парною, ні непарною.

г) Точки розриву та вертикальні асимптоти знайдемо з умови , або ; . Отже, є дві точки розриву другого роду, т.я. , та дві асимптоти і .

д) Перевіримо поведінку функції в нескінченності. Для цього обчислимо:

, при цьому значення функції залишається весь час від’ємним;

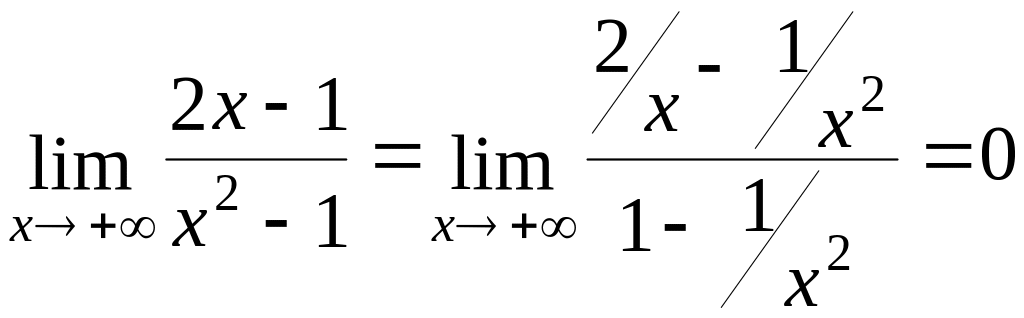, але значення функції залишається весь час додатнім.

Отже, - горизонтальна асимптота для нескінченностей.

Похилу асимптоту, якщо вона існує, будемо шукати у вигляді прямої , де

, а .

,

отже, і знову приходимо до висновку, що існує тільки горизонтальна асиптота - вісь OX, а похилих не існує.

е) Для знаходження екстремумів функції та інтервалів монотонності знайдемо похідну

Похідна не існує в точках , але вони не належать області визначення.

, якщо . Але , тому критичних точок функція не має, а отже і екстремумів - також.

З цього можна зробити висновок, що функція спадаюча у всій області визначення.

Дійсно, якщо , то , функція спадає;

якщо , то , функція спадає;

якщо , то також ,а значить, функція є спадною.

є) Для визначення точок перегину та інтервалів опуклості та вгнутості, знайдемо другу похідну:

при , отже рівняння можемо розв’язати графічно, побудувавши в одній системі координат графіки функцій та та знайшовши абсциси їхніх точок перетину.

Малюнок № 1.

Дійсно, т.я. абсциса точки перетину близька до нуля, то в рівнянні вираз при , значить , отже . Отже, точка перетину наближена до точки .

не існує при , але ці точки не належать області визначення. Отже, вважаємо що точка - єдина критична точка.

Маємо:

якщо , то , крива опукла,

якщо , то , крива вгнута,

якщо , то , крива опукла,

якщо , то , крива вгнута.

ж) Враховуючи проведене дослідження, будуємо графік функції .

Малюнок №2