
Очередная шпора по физике )
.doc№1. Эл/ст поле в вакууме. З-н Кулона. Пр-п суперпозиции д/Е. Поле с-мы точ. зарядов.
В природе сущ. 2 вида заряд: (+) и (-). Точечн заряд—заряженный объект, размерами кот м/пренебречь. Д/точеч. заряд справедлив з-н Кулона: F=k*|q1|*|q2|/r2, В СГС: k=1
If у нас есть заряд q и на него действует сила эл/ст природы, тгд мы говорим, что заряд попал в эл/поле. F=q*E. E — напряж-ть эл. поля (сила, действ-я на единичный неподвижный пробный заряд, н-ся напряж-тью эл. поля) EA=k*q*r/r3 if q>0, то E↑↑r
Пр-п суперпозиции: Напряж-ть эл/поля E неск неподвижных зарядов q1, q2... =на в-орной сумме напряж-тей полей, кот создавал бы кажд из этих зарядов в отсут остальных, т.е. E=∑qi/(ri)3*ri Где ri — радиус-в-ор, проведённый из заряда qi в т наблюдения. Д/наглядного изобр-я эл/полей исп-ся силовые линии (линия, напр-е касательной к кот в кажд т, через кот она проходит, совпадает с напр-ем в-ра E в той же т). Эл/силовые линии нач-ся от положит зарядов и оканч-ся на отриц. В пр-ве, свободном от эл/зарядов, силовые линии там гуще, где поле E сильнее, и реже там, где оно слабее.
№2. Поток в-ра Е. Теор Гаусса д/Е.
И![]() нт-л
Ф=∫E
dS
н-ют потоком в-ра напряж-ти эл/поля Е.
Теор Гаусса
опр-т поток в-ра напряж-ти эл/поля через
произв замк пов-ть S.
За положит нормаль к пов. S
примем внеш нормаль, те нормаль напр-ю
наружу. Ф=∫EndS≈∑Ei
cosαi
∆Si
Матем поясн:
∆Ω=∆S/r2≈∆S┴/r2,
справедливо при малых углах. Возьмём
Точечн заряд. ∆Фi=kq/(ri)2*
cosαi
∆Si=kq/(ri)2*∆Si┴=kq
∆Ωi
нт-л
Ф=∫E
dS
н-ют потоком в-ра напряж-ти эл/поля Е.
Теор Гаусса
опр-т поток в-ра напряж-ти эл/поля через
произв замк пов-ть S.
За положит нормаль к пов. S
примем внеш нормаль, те нормаль напр-ю
наружу. Ф=∫EndS≈∑Ei
cosαi
∆Si
Матем поясн:
∆Ω=∆S/r2≈∆S┴/r2,
справедливо при малых углах. Возьмём
Точечн заряд. ∆Фi=kq/(ri)2*
cosαi
∆Si=kq/(ri)2*∆Si┴=kq
∆Ωi
Ф=∑Ei cosαi ∆Ωi =kq∑∆Ωi=kq*4π
If q<0, то никаких минусов писать не надо (ф-ла всё равно правильная). If зар. лежит во внеш. пр-ве по отн-ю к пов-ти S, то его поток =ен 0. В результате получ-ся следующее фундаментальное соотн-е: Ф≡∫(EdS)=4πQ Наз-ое эл/ст теор Гаусса. Здесь Q — алгебр сумма всех зарядов, окружённых замкнутой пов-тью S.
№3. Циркуляция в-ра Е. Пот-л.
Ц![]() иркуляция
в-ра Е н-ся инт-л ∫ Еl
dl.
Док-м, что он =ен 0. Док-во: Возьмём Точечн
заряд q>0.
Eldl=q/r2*dlcosα
иркуляция
в-ра Е н-ся инт-л ∫ Еl
dl.
Док-м, что он =ен 0. Док-во: Возьмём Точечн
заряд q>0.
Eldl=q/r2*dlcosα
![]()
Из этого выраж-я => т-ма о циркуляции: r1=r2 инт-л ∫ Еl dl=0
В-орное поле Е н-ся пот-льным, if циркуляция в-ра Е по люб замк контуру =на 0.
Д/пот-льных полей м/ввести понятие пот-ла, или точнее, разности пот-лов. Разностью пот-лов φ1–φ2 между тт 1 и 2 н-ся работа, соверш-ая силами поля при перемещении единичного полож заряда по произв пути из т 1 в т 2.
![]()
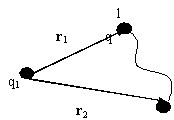
q(φ1–φ2) =q*(q1/r1- q1/r2), φ1= q1/r1+const, φ2= q1/r2+const. (чаще сonst= 0, на бск φ=0
Пр-п суп. позиции д/пот-ла (след. из пр. суп. д/Е)
Аэл.=q(φA–φB)= q(φ1A–φ1B)+ q(φ2A–φ2B)+…
φA= φ1A+φ2A+φ3A+…, φB= φ1B+φ2B+φ3B+…
№4. Эквипот-ые пов-ти. Связь напряж-ти эл/ст поля и пот-ла.
С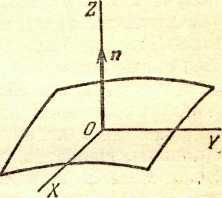 вязь
E
и φ.
вязь
E
и φ.
![]() =>
=>
![]() ,
,
![]()
![]() ,
,
![]() ,т.е.
,т.е.
![]() , где
, где
![]() (1)
(1)
Эквипот-ая
пов-ть
-
такая пов-ть, на кот пот-л
остается const.
Он м/меняться
только при переходе от одной эквипот-ой
пов-ти к др. Возьмем
на эквипот-ой пов-ти произв т О и введем
лок с-му
коорд с началом в этой т (рис.). Ось Z
направим по
нормали
n
к
эквипот-ой пов-ти
в стор возраст-я пот-ла φ.
То
же напр-е примем за положит напр-е нормали
n.
Коорд пл-ть
XY
совместится с касательной
пл-тью к эквипот-ой пов-ти. Тгд в
т О
дφ/дх
= дφ/ду=0.
Кр того,
k=n,
дφ/дz
≡ дφ/дn.
Ф-ла (1)
→
![]() .
Ф-я
φ
возрастает наиб быстро в напр-ии нормали
n,
поэт
градиент
ф-ии φ
(х,
у, z)
есть в-ор, напр-ый в стор max возраст-я
этой ф-ии, а его длина =на производной
ф-ии φ
в том
же напр-ии. Это
опр-е носит инвариантный
хар-р, те
никак не связано с выбором с-мы коорд.
.
Ф-я
φ
возрастает наиб быстро в напр-ии нормали
n,
поэт
градиент
ф-ии φ
(х,
у, z)
есть в-ор, напр-ый в стор max возраст-я
этой ф-ии, а его длина =на производной
ф-ии φ
в том
же напр-ии. Это
опр-е носит инвариантный
хар-р, те
никак не связано с выбором с-мы коорд.
В-ор E напр-н противоположно в-ору градиента пот-ла φ. Эл/силовые линии явл, то, линиями, вдоль кот пот-л φ изм-ся наиб быстро. Они нормальны к эквипот-льным пов-тям. Поэт эквипот-ые пов-ти м/служить д/наглядного изобр-я картины поля.
№![]() 5. Пров-ки в эл/ст
поле.
5. Пров-ки в эл/ст
поле.
1)
![]() В кажд т внутри пов-ти
В кажд т внутри пов-ти
2)
![]()
![]()
![]() .
.
![]()
![]()

![]() =>
=>
![]() Пров-ки в эл-ке представляют эквипот.
объем, а пов-ть пров-ка явл-ся эквипот.
пов-ю.
Пров-ки в эл-ке представляют эквипот.
объем, а пов-ть пров-ка явл-ся эквипот.
пов-ю.
3) Эл/заряды сущ-ют (м/сущ-ть) только на пов-ти пров-ка
4) Сущ-ет
связь между напр. эл/поля вблизи гран.
пров-ка и плотн-ю зар. на пов-ти. Выберем
сплюсн. парал-д, д/этой пов-ти:![]() ,где
Q-заряд
окруж. пов-ю инт-я.
,где
Q-заряд
окруж. пов-ю инт-я.![]() =>
=>
![]() - напр. поля вблизи мет. в проекц. на
нормаль. Проекция Е берется из мет. в
вакуум. Поле в т. 1 созд. всеми зарядами,
но выраж. только через те зар., кот.
распол. поблизости.
- напр. поля вблизи мет. в проекц. на
нормаль. Проекция Е берется из мет. в
вакуум. Поле в т. 1 созд. всеми зарядами,
но выраж. только через те зар., кот.
распол. поблизости.
5)
Поле в полости
т.е. поле внутри полости =0. Проверка:1)Т.к.
![]() то линий внутри полости быть не может,
т.к. получится, что
то линий внутри полости быть не может,
т.к. получится, что
![]() - разные 2) Сил. линии д/обрываться на
минусе, но его нет. 3) Замкн. линий тоже
нет.
- разные 2) Сил. линии д/обрываться на
минусе, но его нет. 3) Замкн. линий тоже
нет.
№6 Теор о ед-ти р-я задач электростатики.
П: задано распр-е пров-ков и их полные заряды, тгд напряж-ть эл/поля в кажд т нах-ся единственным образом.
Док
(от противного): П :
возм/др распр-е зарядов на пров-ках:
:
возм/др распр-е зарядов на пров-ках:
![]() ,
след-но, возм/сущ-е 2-х различных в-оров
Е в 1-ой т (Е=4πσ). Значит,
,
след-но, возм/сущ-е 2-х различных в-оров
Е в 1-ой т (Е=4πσ). Значит,
![]() и соотв им заряды –q1,
–q2,
–q3,
кот создают такое же поле, но противоп
по напр-ю. Перераспределим заряд на
пров-ках:
и соотв им заряды –q1,
–q2,
–q3,
кот создают такое же поле, но противоп
по напр-ю. Перераспределим заряд на
пров-ках:
![]() В общем сл получим
В общем сл получим
![]() но тгд
но тгд
![]() Проанализируем по картинкам: Во всех
возм сл наруш-ся теор о циркуляции д/в-ра
Е!
Проанализируем по картинкам: Во всех
возм сл наруш-ся теор о циркуляции д/в-ра
Е!
1)![]() 2)
2)![]() 3)
3)![]()
№ 8 Связь между плотностью заряда на пов-ти пров-ка и полем вблизи него.
Рассм некот заряж-ю
пов-ть S.
![]() Полупр-во
по одну стор этой пов-ти обозначим
индексом 1, а по другую – индексом 2.
Пов-ая плотность заряда σ м/меняться
вдоль пов-ти S
произвольно. Возьмём бск малый цил,
основания кот располож по разн стор от
S.
Высота цила д/б << л/размеров его
оснований. П: площадь его оснований =на
∆S,
тгд внутри цила нах-ся эл/заряд q=σ∙∆S.
Сумма потоков в-ра Е через основания
цила б/=на
Полупр-во
по одну стор этой пов-ти обозначим
индексом 1, а по другую – индексом 2.
Пов-ая плотность заряда σ м/меняться
вдоль пов-ти S
произвольно. Возьмём бск малый цил,
основания кот располож по разн стор от
S.
Высота цила д/б << л/размеров его
оснований. П: площадь его оснований =на
∆S,
тгд внутри цила нах-ся эл/заряд q=σ∙∆S.
Сумма потоков в-ра Е через основания
цила б/=на
![]() .
Поток через бок пов-ть цила пренебрежимо
мал. Тгд по теор Гаусса получаем
.
Поток через бок пов-ть цила пренебрежимо
мал. Тгд по теор Гаусса получаем
![]() ,
значит,
,
значит,
![]() .
Получим:
.
Получим:
![]() .
Проецируя поля Е1
и Е2
на одну общую нормаль n,
получим Е2n—Е1n=4πσ.
То, при переходе через заряж-ю пов-ть
нормальная составляющая в-ра Е претерпевает
скачок, равный 4πσ. Происхождение скачка
м/объяснить с др т зрения. Полное эл/поле
в люб т пр-ва склад-ся из внутр поля
Евнутр,
т.е. поля, создаваемого зарядами самой
площадки ∆S,
и внеш поля Евнешн,
т.е. поля, создаваемого всеми остальными
зарядами. При пересечении площадки ∆S
внеш поле меняется непрерывно. А площадку
∆S
на бск малых расст-ях от себя м/рассм,
как бск заряж-ю пл-ть. Создаваемое ею
поле перпенд-но к площадке и =но 2πσ.
Однако напр-я этого поля в 1-ой и во 2-ой
областях различны. Т.о., получим
.
Проецируя поля Е1
и Е2
на одну общую нормаль n,
получим Е2n—Е1n=4πσ.
То, при переходе через заряж-ю пов-ть
нормальная составляющая в-ра Е претерпевает
скачок, равный 4πσ. Происхождение скачка
м/объяснить с др т зрения. Полное эл/поле
в люб т пр-ва склад-ся из внутр поля
Евнутр,
т.е. поля, создаваемого зарядами самой
площадки ∆S,
и внеш поля Евнешн,
т.е. поля, создаваемого всеми остальными
зарядами. При пересечении площадки ∆S
внеш поле меняется непрерывно. А площадку
∆S
на бск малых расст-ях от себя м/рассм,
как бск заряж-ю пл-ть. Создаваемое ею
поле перпенд-но к площадке и =но 2πσ.
Однако напр-я этого поля в 1-ой и во 2-ой
областях различны. Т.о., получим
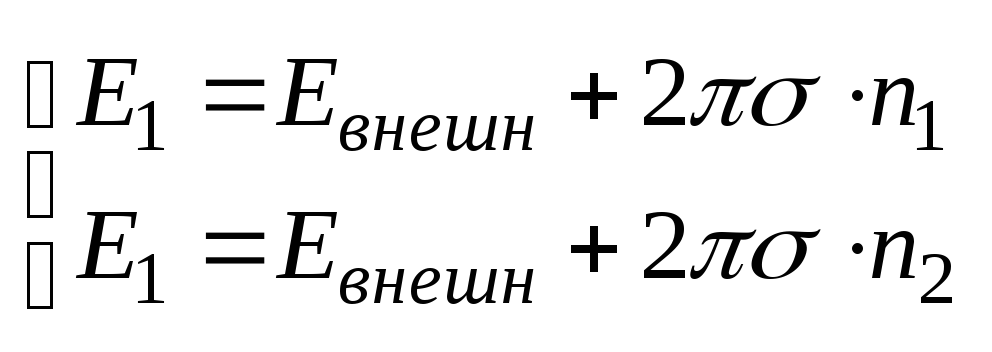 (*).
Итак, мы выяснили, что скачок терпит
только внутреннее поле самой площадки,
а т.к. внутреннее поле не имеет
тангенциальной составляющей и внеш
поле меняется непрерывно, то
(*).
Итак, мы выяснили, что скачок терпит
только внутреннее поле самой площадки,
а т.к. внутреннее поле не имеет
тангенциальной составляющей и внеш
поле меняется непрерывно, то
![]() .
Из ф-лы (*) также =>
.
Из ф-лы (*) также =>
![]()
№ 9. Р-е эл/ст задач
методом эл/ст изобр-ий.
9. Р-е эл/ст задач
методом эл/ст изобр-ий.
К изначально незаряж, бск слою металла поднif положит заряд на расст а от него. Тгд на пов-ти металлич слоя выступит неравномерно распр-ый заряд –q, с плотностью распр-я σ(x). Д/расчёта поля, вне металла заряд, индуц-ый на пов-ть металла, м/заменить мнимым зарядом q΄=-q, располож в толще металла на таком же расст-и а.
Р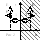 ассм
теперь поле только зарядов, индуц-ых на
пов-ть металла. Выберим тт 1 и 2 вблизи
пов-ти металла, но лежащие по разные
стор от неё. В силу близости этих тт,
тангенц составл-ая поля сохранится, а
нормальная – изменяет своё напр-е, но
не велич. Это => из пр-па суперпозиции.
Получили с-му:
ассм
теперь поле только зарядов, индуц-ых на
пов-ть металла. Выберим тт 1 и 2 вблизи
пов-ти металла, но лежащие по разные
стор от неё. В силу близости этих тт,
тангенц составл-ая поля сохранится, а
нормальная – изменяет своё напр-е, но
не велич. Это => из пр-па суперпозиции.
Получили с-му:
 .
Это поле эквивалентно полю двух точеч
зарядов, располож на одинак расст-и от
плоск-и. Один заряд – тот, который поднif,
а др – мнимый, нах-ся в толще металла.
Такая замена н-ся методом изобр-ий.
.
Это поле эквивалентно полю двух точеч
зарядов, располож на одинак расст-и от
плоск-и. Один заряд – тот, который поднif,
а др – мнимый, нах-ся в толще металла.
Такая замена н-ся методом изобр-ий.
№ 10. Кондр-ы.
Кондр-ы: представляют собой пластины, разнесённые на некот расст-е d, кот << размеров самих пластин. На кажд из них нах-ся заряд, кот и опр-т эл/поле между обкладками.
φ1
> φ2 φ1
- φ2
= U
E
~ q
→ U
~ q.
![]() .
.
![]()
Примеры выч-я
ёмкости конд-ров: 1) Плоский конд-р. σ=q/s.
E=4πσ
=> n=Ed.
En=
4πσ.
U=∫Eldl=Ed.
C=q/(Ed)= S/(4πd)
– СГС.
С=
ε0S/d.
2) Сферич
конд-р:
E=q/r2,
φ1-φ2=
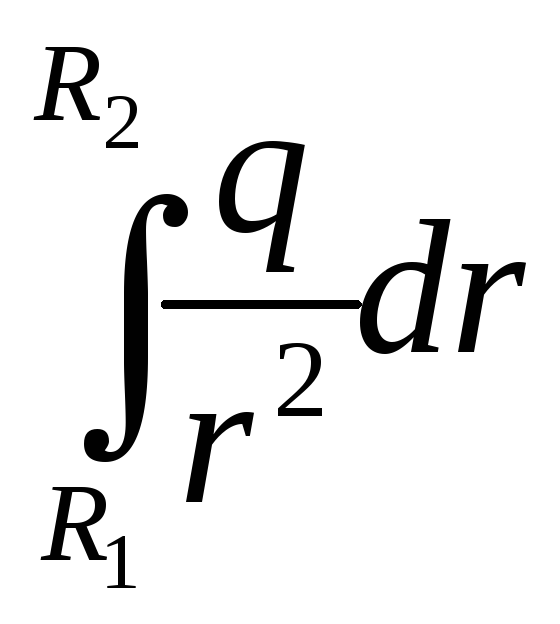 =
q(1/R1-1/R2).
C=q/U=
R1R2/(R2-R1)
=
q(1/R1-1/R2).
C=q/U=
R1R2/(R2-R1)
Соед-е кондр-ов: 1) паралл. U1= U2=U, q= q1+q2. C=q/U= (q1+q2)/U= C1+C2 2) послед. С=q/(U1+U2)= q/(q/C1+q/C2)= C1C2/(C1+C2), 1/C= 1/C1+1/C2+1/C3...
№11. Энергия с-мы точеч зарядов. Энергия заряженного проводника и конд-ра. Плотность энергии эл/поля.
Энергия с-мы точ зарядов: П: точеч заряды q1 и q2 нах-ся в вакууме на бск расст друг от друга. Чтобы их сблизить до расст-я r12, надо затратить работу (q1q2)/r12. Пот-я энергия взаимод-я зарядов б/U=(q1q2)/r12. Д/неск точеч зарядов: U=(1/2)∑∑ (qiqk)/rik (i≠k). Коэф-т ½ поставлен, тк при суммировании пот-я энергия кажд пары учитывается дважды. Ф-лу м/представить в виде: U=(1/2) ∑φiqi где φi - пот-л в т нах-я i-го заряда, созд-ый всеми зарядами: φi=∑qk /rik .
-
Энергия заряженного конд-ра: Энергия зар-го конд-ра опр-ся зарядами его обкладок и разностью пот-лов между ними. Б/переносить полож эл-во б.м. порциями dq с отриц обкладки на полож. Д/переноса dq необх совершать работу против эл/поля: δAвнеш=φdq где φ – мгновенное знач-е разности пот-лов между обкладками. Работа самого конд-ра б/такой же по велич, но противоп по знаку: δA=-φdq. Работа целиком пойдёт на увелич-е эл/энергии конд-ра W, т.е. dW= φdq=qdq/C, т.к. ёмкость остаётся пост, то инт-я получаем: W=q2/2C=1/2φq=1/2Cφ2
-
Энергия с-мы заряженных пров-ков: Рассм с-му неск тел произв формы с зарядами q1, q2, q3,.. и пот-лами φ1, φ2, φ3,.. Примем за начальное такое сост-е, в кот все тела не заряжены. Б/переносить эл-во из бск на эти тела б.м. порциями. Так же, как в случ конд-ра, найдём : W=∫∑φi’dqi’ где сумм-е ведётся по всем телам. Штрихи означают, что эти величины переем-е, мен-ся в процессе зарядки. П: qi и φi – заряд и пот-л i-го тела в конечном сост-и. Осуществим зарядку так, чтобы в люб мом времени перем-е заряды qi’ б/пропорц их конечным знач-ям qi : qi’=k qi где k – переем-я велич, одинак д/всех qi . Во время зарядки k возраст от 0 до 1. Тк D=ξE : φi’=k φi . Очевидно: k – переем-я инт-я, и dqi’= qidk, и W=∑ φiqi
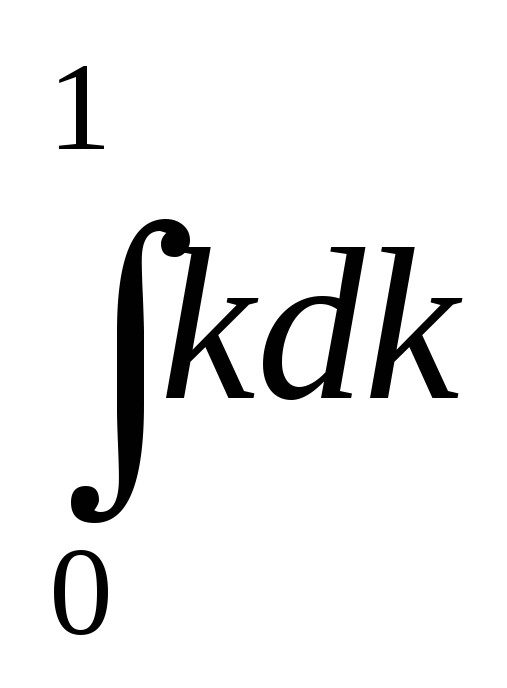 ,
выполнив
инт-е, получим: W=1/2∑
φiqi
.
,
выполнив
инт-е, получим: W=1/2∑
φiqi
.
№12. Дипольный мом молек. В-ор поляризации.
∑qn+=q+=q>0 - в атоме (эл/нейтр с-ма), ∑qn-=q-= -q>0
p - дипольный мом (не зав от выбора нач коорд)
p=∑qnrn=∑qn+rn + + ∑qn-rn-= q(r+ - r-) где r+ - r- = l - плечо диполя (пров-ся из ‘–‘ в ‘+’). p= ql.
P= (∑pi)/(dV) - в-ор поляризации (pi – дипольн мом-т i-ой молек), [P]= [E]СГС
№ 13. Теор Гаусса
д/в-ра P.
P=∑pi/∆V.
Участок ∆S
маленький так, что p
одинак у всех молек. Возьмём призму на
гр-це. N
– число молек (диполей) в 1 куб см. Pn∆S=
pNcosα∆S=
q(lcosα∆S)N.
P=Np.
П: cosα>0.
Pn∆S=-dqсвяз.
13. Теор Гаусса
д/в-ра P.
P=∑pi/∆V.
Участок ∆S
маленький так, что p
одинак у всех молек. Возьмём призму на
гр-це. N
– число молек (диполей) в 1 куб см. Pn∆S=
pNcosα∆S=
q(lcosα∆S)N.
P=Np.
П: cosα>0.
Pn∆S=-dqсвяз.
![]() =-Qсвяз.
=-Qсвяз.
№ 14. В-ор эл/инд-ии D. Теор Гаусса д/D. Влияние диэл-ка на эл/поле сводится к действию поляризационных зарядов. По теор Гаусса: ∫EndS=4π(q+qпол). Поскольку qпол =-∫PndS, то получаем ∫(En+4πPn)dS=4πq.
Введём новый в-ор D=E+4πP, н-ый в-ором эл/индукции. Тгд ∫DndS=4πq. Это есть теор Гаусса д/в-ора D. В диф-ой ф-ме она выглядит так: DivD=4πρ, где ρ – объемная плотность своб зарядов.
№ 15. Л/среды. Связь между P и E, E и D. Опыт показывает, что д/обширного класса диэл-ков и связь между в-орами P и E линейна. Это объясняется тем, что напряж-ти макроскопич эл/полей обычно оч малы по сравн с напряж-ми микрополей внутри атомов и молек. If среда изотропна, то в-оры P и E коллинеарны и м/написать: P=αE, где α – безразмерный коэф-т, н-ый поляризуемостью диэл-ка. Он зависит от плотности и температуры диэл-ка. Связь между D и E м/записать в виде D=εE, безразм велич ε=1+4πα н-ся диэл/проницаемостью диэл-ка. Этой величиной обычно характ-ся индивидуальные св-ва диэл-ков. Д/вакуума α=0, ε=1.
№ 16. Механ
поляризации диэл-ков с неполярн и полярн
мол. Заряды
диэл-ка м/смещаться из своих полож равнов
лишь на небольшие расст-я. Допустим, что
диэл-к сост из эл/нейтральных молек. Под
действием приложенного эл/поля центр
тяжести электронов в молек смещается
отн центра тяжести атомных ядер. Молек
становятся эл/диполями, ориент-ми положит
заряж концами в напр-ии эл/поля Е.
В![]() этом случ говорят, что диэл-к поляризован,
а само смещение полож и отриц зарядов
диэл-ка в направлении эл/поля Е
н-т эл/поляризацией. На схематическом
рисунке диэл-к изображен в виде
прямоугольника, а молек – в виде кружков.
(+) - чёрный цвет, (-) - белый. На конце AB
параллелепипеда ABCD
выступают нескомпенсированные отриц,
а на конце CD
положит поверхностные заряды. Это и
есть индукционные заряды, появляющиеся
в результате поляризации диэл-ка. Их
н-т связ зарядами.
этом случ говорят, что диэл-к поляризован,
а само смещение полож и отриц зарядов
диэл-ка в направлении эл/поля Е
н-т эл/поляризацией. На схематическом
рисунке диэл-к изображен в виде
прямоугольника, а молек – в виде кружков.
(+) - чёрный цвет, (-) - белый. На конце AB
параллелепипеда ABCD
выступают нескомпенсированные отриц,
а на конце CD
положит поверхностные заряды. Это и
есть индукционные заряды, появляющиеся
в результате поляризации диэл-ка. Их
н-т связ зарядами.
Механизм поляризации диэл-ка м/б и иным. Сущ-т диэл-ки, молек кот обладают дипольным мом-ом и в отсутствие внеш полей. Такие молек н-ся полярными. If поля нет, то полярные молек совершают хаотич тепл дв-я и ориент-ны беспорядочно. При наложении эл/поля дипольные мом-ты молек ориент-ся преимущественно в напр-ии поля. А это означает, что диэл-к становится поляризованным.
№ 17. Гу д/в-ов E
и D.
Из теор Гаусса д/в-ора D
м/вывести гу. Рассм границу S
двух диэл-ков. Возьмём бск малый цил,
основания кот располож по разные стор
от S.
If площадь основания ΔS,
то внутри цила нах-ся заряд q=σΔS.
Сумма потоков в-ора D
через основания цила б/ (Dn1+Dn2)
ΔS,
поток через бок пов-ть пренебрежимо
мал. П![]() риравнивая
это выраж-е величине 4πσΔS,
получим Dn1+Dn2=4πσ.
Выберем единую нормаль n
к пов-ти S.
Направим её из среды 1 в среду 2. Тгд
D2n-D1n=4πσ.
Аналог м/док, что E2n-E1n=4π(σ+σсвяз).
При это тангенц сост-я в-ора E
не меняется (Eτ1-
Eτ2=0).
Это м/объяснить так: полное поле в любой
т м/представить в виде суммы поля Eвнутр,
создаваемого поверхн зарядом площадки
ΔS,
и поля Eвнешн,
создаваемого всеми остальными зарядами.
При пересечении площадки поле Eвнешн
остаётся
непрерывным, а значит, не меняется Eτ.
риравнивая
это выраж-е величине 4πσΔS,
получим Dn1+Dn2=4πσ.
Выберем единую нормаль n
к пов-ти S.
Направим её из среды 1 в среду 2. Тгд
D2n-D1n=4πσ.
Аналог м/док, что E2n-E1n=4π(σ+σсвяз).
При это тангенц сост-я в-ора E
не меняется (Eτ1-
Eτ2=0).
Это м/объяснить так: полное поле в любой
т м/представить в виде суммы поля Eвнутр,
создаваемого поверхн зарядом площадки
ΔS,
и поля Eвнешн,
создаваемого всеми остальными зарядами.
При пересечении площадки поле Eвнешн
остаётся
непрерывным, а значит, не меняется Eτ.
№ 18. Энергия эл/поля при налич диэл-ков. Плотность энергии эл/поля. Выразим эл/энергию диэл-ка через в-оры E и D. Выч-им элементарную работу δ*Aвнешн, кот производят внеш силы при квазистатич проц-е электризации диэл-ка. Возьмём в изотропном диэл-ке 2 бск малые плоские площадки AB и CD, перпенд к эл/полю E. Расст-е между ними предполагается бск малым высшего порядка по сравн с их л/размерами. П: эл/силы, напр-е против эл/поля E, переносят с площадки AB на площадку CD эл/заряд δq=Sδσ. Тгд δ*Aвнешн= δqEl= SlEδσ= Veδσ
В результате такого переноса (по теор Гаусса) эл/поле изм-ся только между площадками, а вне их всюду останется неизменным. Длина в-ора D между площадками изменяется на величину δD= δ(E+4πP)= 4πδP= 4πδσпол, так что д/δ*Aвнешн получим δ*Aвнешн=(1/4π)VEdD. Поделим это выраж-е на объём δAвнешн= (1/4π)EdD. Эта ф-ла б/давать приращение плотности эл/энергии W. Плотнось энергии W м/найти как инт-л W=(1/4π)∫EdD.
№ 19. Поверхностная плотность силы, действующей на границе металла. f – сила, действ-я на 1 куб см диэл-ка (плотность силы)
f= n(p▼)E= (P▼)E= (ε-1)/4π (E▼)E= (ε-1)/8π grad E2
№ 20. Объемная
плотность силы,
действующей на диэл-к в эл/полях. (F,
E,
l,
f,
p,
P,
орта – все это в-ора). F
= qE++
(-q)E_
- сила действ-я на диполь. Е+
- напр-е внеш поля в т нах-я заряда q>0.
![]()
![]()
Сила действ-я на 1 см куб – плотность силы. f – сила действ-я на 1 см куб. в-ва диэл-ка, n – число диполей в 1 см куб.
![]() ,
т.к
,
т.к
![]() ,
,
![]()
![]() .
.
№ 21. З-н Био-Савара-Лапласа. Он опр-ет м/поле дв-ся точ зар q. B=q/cr3*[vr], где r – р-в-ор из т наблюд к q, с – коэф пропорц (зав от с-мы коорд). Учитывая E=q*r/r3: B=1/c*[vE]. Рассм 2 дв-ся зар. Поле от q1 в т q2: B=q1/cr312*[v1r12] и сила: F12= q2/c*[v2B1]= (q1q2)/(c2r312)[v2[v1r12]], аналог д/q2. М/поле объёмного эл-та тока: dB=[jr]/сr3*dV, аналогично д/линейного: dB=(J[dlr])/(cr3). Полное поле нах-ся инт-ем по всем токам: B=1/с∫[jr]/r3*dV и B=∫(J[dlr])/(cr3) (послед - по замкн контуру).
№22 Поле прямого провода.
М /поле
эл-та тока Jdl
/поле
эл-та тока Jdl
![]() М/линии
– окр-ти, с центром на оси провода
М/линии
– окр-ти, с центром на оси провода
В скал ф-ме
![]()
![]()
![]() If провод бск, то
If провод бск, то
![]() ,
а
,
а
![]() =>
=>
![]()
№23 Поле на оси соленоида
1) Поле витка с током
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ;
x>>R=>
;
x>>R=>
![]()
 2)
Поле катушки
2)
Поле катушки
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
№24 Сила Лоренца и сила Ампера

![]() ,
if
есть E=>
,
if
есть E=>![]()
![]() ,
j=qnv,
,
j=qnv,
![]()
![]()
Сила, действ-я на провод конечной длины
![]()
№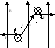 25. Момент сил,
действующих на виток с током в магнитном
поле.
25. Момент сил,
действующих на виток с током в магнитном
поле.
Рассм однор м/поле. S=ab – площадь рамки. F1=F2= i/c*Ba. M= (i/c)Ba(b/2)cosα*2= (i/c)BScosα. M=[pм, B], где pм= (i/c)Sn (n – единич нормаль).
Опыт: виток развор-ся нормалью по полю и втяг-ся в обл сильн поля.
№ 26.
Теор о цирк в-ора В.
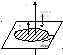
26.
Теор о цирк в-ора В.
Возьмём на контуре малое dl. B=(2i)/(cr) – д/бск провода. Bldl= Bdlcosα= Brdφ= (2irdφ)/(cr), где r – расст от провода до dl, dφ – угол от нач dl к концу dl.
![]()
Д/невыпуклого контура угол всё равно возраст монотонно (тк кое-какие углы берём 3 раза и 2 - компенсируются). Ток вне контура не вносит вклада, тк там углы полностью компенсируются. Д/неплоского контура та же ф-ла, тк не важна высота, а только угол в плоскости, перпенд пров-ку. При неск токах они склад-ся алгебраически (только те, что охвачены контуром!).
№ 27. Теор о цирк в-ора
I.
N
– число молек в 1 куб см. If
ядро атома попадёт в цилл, то его ток
пересеч штрихов обл 1 раз (иначе либо не
пересечёт, либо 2-жды). dV=Sdlcosα.
diмол=
i1молNSdlcosα=
CIdlcosα.
27. Теор о цирк в-ора
I.
N
– число молек в 1 куб см. If
ядро атома попадёт в цилл, то его ток
пересеч штрихов обл 1 раз (иначе либо не
пересечёт, либо 2-жды). dV=Sdlcosα.
diмол=
i1молNSdlcosα=
CIdlcosα.
∫Ildl=iмол/c (iмол – полн ток с учётом знака. Инт-л по контуру L).
№ 28. Напряж-ть м/поля. Теор о цирк в-ра Н. I – в-ор намаг-ти. B=H+4πI, где Н – в-ор напряж-ти м/поля. Н=В-4πI, Н не имеет разм-ти. ∫Bldl=(4π/с)∑(i+iм) (везде инт-л по замк контуру L), где ∑i – токи пров-ти, ∑iм – молек токи. (4πiм)/с= ∫4πIldl, ∫(Bl-4πIl)dl= (4π)/c*∑i. ∫(H)ldl= (4π)/c*∑i.
№ 29. Л/среды. Связь в-ов B, H, I. I=æH (æ<<1), I=æB (верно вне в-ва). Это верно д/парамаг-ов и диамаг-ов. B=H+4πI – вып-ся всегда. B=H+4πæH= μH, μ=1+4πæ, æ=(μ-1)/(4π). æ – м.восприимч-ть, μ – м/прониц-ть, I – в-ор намаг-ти, H – в-ор напряж-ти м/поля.
№ 30. Гу д/в-оров B и H.
1 )
∫B
)
∫B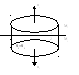 ndS=0
– всегда. S1,
S2
– малы, так что B=const.
Sбок<<S1.
Тгд
B1n1S1+
BcpSбок+
B2n2S2=0
=> B1n=B2n
ndS=0
– всегда. S1,
S2
– малы, так что B=const.
Sбок<<S1.
Тгд
B1n1S1+
BcpSбок+
B2n2S2=0
=> B1n=B2n
2)
![]()
а) iпов=0, l – малы (H=const), ∆l<<1: H1l1l+ Hср2∆l+ H2l2l=0 => H1τ= H2τ
