1.Пузырьковый режим; 2. Расслоенный; 3. Волновой; 4. Пробковый

5. Пленочно-диспергированный; 6. Кольцевой; 7. Эмульсионный

Приём, критерий Фруда для смеси находится по формуле:

(246)

Недостатками большинства приведённых диаграмм является то, что они получены для узкого интервала условий давлений и температур (близких к стандартным), на модельных смесях (в основном водо – воздушных) в ограниченном диапазоне поперечных сечений трубопровода.

Границы между различными режимами достаточно условны, поскольку взаимопереход различных структур потока, как правило, осуществляется через промежуточные состояния.

Тем не менее существуют многочисленные аналитические и графические зависимости с помощью которых авторы предлагают определять границы существования того или иного режима.

Так, А.И.Гужов для горизонтальных и нисходящих трубопроводов, транспортирующих реальные газо-нефтяные смеси, в области перехода от пробкового к расслоенному режиму предлагает пользоваться следующим соотношением:

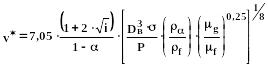(247)

В области перехода от пробкового к пленочно – диспергированному режиму для труб произвольно ориентированных в пространстве (кроме вертикальных):

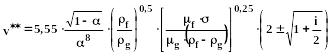(248)

где: и - критическая скорость;

- гидравлический уклон трубопровода;

- среднее давление в трубопроводе;

- плотность смеси при расходном газосодержании:

(249)

При режим течения расслоенный;

при < режим течения пробковый;

при режим течения пробковый;

при < режим течения пленочно – диспергированный.

Д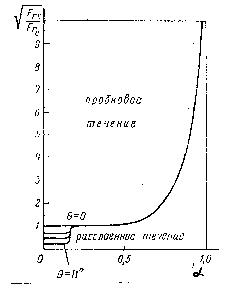 ля горизонтальных и слабонаклоненных трубопроводов ( <11⁰) можно воспользоваться следующей графической зависимостью (рис.37):

Рис.37. Диаграмма структуры потока для

горизонтальных и слабонаклонных потоков.

где:

(250)

Для восходящих и вертикальных трубопроводов можно воспользоваться следующей шрафической зависимостью (рис.38):

Р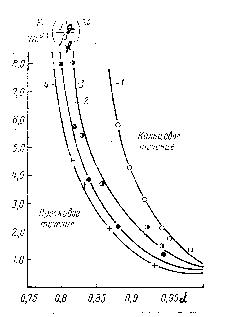 ис.38. Диаграмма структуры потока для

восходящих и вертикальных трубопроводов

1. =0,001 Па^.с; 2. =0,017 Па^.с; 3. =0,043 Па^.с; 4. =0,137 Па^.с

Критерий Вебера ( ) находится по формуле:

(251)

Пузырьковый режим

Для пузырькового режима характерно присутствие отдельных пузырьков в непрерывной жидкой среде. Область объёмных газосодержаний, соответствующих пузырьковому течению, простирается от одиночного изолированного пузырька до сплошного течения пены, когда на долю жидкости приходится менее 1 % объёма.

Имеется множество разновидностей пузырькового течения. Они различаются концентрацией пузырьков, их размерами, распределением по сечению и взаимодействием между собой, жидкостью и стенками.

Устойчивый пузырьковый режим встречается редко, т.к.он самопроизвольно стремится перейти в другие режимы (в основном, в пробковый или расслоенный).

Способы получения пузырькового режима и его основные свойства:

1. Вдув газа в жидкость через отверстия:

Если отверстие невелико, а расход газа мал, то радиус образующихся пузырьков можно оценить с помощью соотношения:

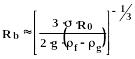(252)

где: - радиус отверстия.

С увеличением радиуса отверстия и расхода газа размеры пузырьков возрастают. Но когда расход газа превысит некую граничную величину, из отверстия начинают истекать не отдельные пузырьки, а сплошная струя газа, которая затем в слое жидкости дробится на отдельные пузырьки. Радиус этих пузырьков примерно в два раза больше радиуса отверстия.

2. Помещение в жидкость поверхности с температурой выше температуры кипения жидкости.

В этом случае:

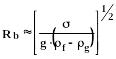(253)

3. Объёмное кипение жидкости или её разгазирование:

В этом случае, пузырьки образуются либо на дефектах стенок, либо на механических примесях.

Размеры пузырьков можно оценить по соотношению Фритца:

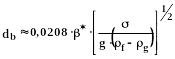(254)

где: - краевой угол смачивания материала стенки жидкостью в градусах.

Если после образования пузырькового режима смесь перемешивать любым способом, то размеры пузырьков могут измениться. Их новый диаметр можно оценить по соотношению Хинце:

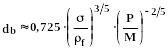(255)

где: - диссипированная механическая мощность, отнесённая к единице массы.

В целом, всегда существует определённое распределение пузырьков по размерам.

Если не предпринимать специальных мер (добавка ПАВ или непрерывное перемешивание), то с пузырьками сразу после их образования начинают происходить самопроизвольные процессы:

1. Любой пузырёк стремится всплыть, т.е. изменить своё первоначальное положение смеси, а, значит, и распределение по сечению трубопровода.

2. Любой пузырёк стремится слиться с соседним или хотя бы агломерироваться с ним (для уменьшения свободной энергии смеси). Обычно, сливаются пузырьки с диаметром превышающим диаметр Хинце, а агломерируются пузырьки с диаметрами меньшими или равными диаметру Хинце. В результате, пузырьковый режим переходит в пробковый.

3. Любой пузырёк стремится лопнуть с образованием непрерывной газовой фазы. В результате, пузырьковый режим переходит в расслоенный.

Скорость движения пузырьков может быть как меньше, так и больше скорости жидкости.

Оценить предельную самопроизвольную скорость движения (подъёма) одиночного пузырька ( ) можно с помощью следующих соотношений:

(256)

Данная зависимость справедлива только если:

В противном случае:

(257)

Данная зависимость справедлива только если:

< (258)

В противном случае:

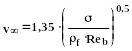(259)

Данная зависимость справедлива только если:

< (260)

В противном случае:

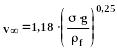(261)

Данная зависимость справедлива только если:

> (262)

где: и - безразмерные комплексы, определяемые соотношениями:

(263)

(264)

Разумеется, реальная самопроизвольная скорость движения пузырьков будет меньше предельной и может быть оценена соотношением Лансберга – Эдгара:

(265)

где:

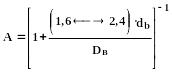(266)

Различие в скоростях газовых пузырьков и жидкости принято называть скоростью дрейфа , которую можно оценить соотношением:

(267)

где: - безразмерный показатель степени, величину которого можно оценить соотношением:

, если

, если

, если >

Таким образом, скорость дрейфа это самопроизвольная линейная скорость всплытия на фоне жидкости, двигающейся в пространстве в произвольном направлении.

Г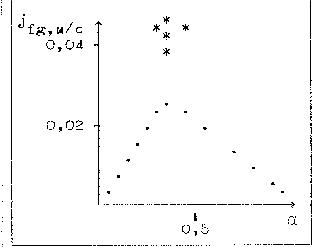 рафически зависимость (267) выглядит следующим образом:

Рис.39. График скорости дрейфа

Из рис.39 следует, что при расходном объёмном газосодержании менее 10 % или более 90 % пузырьки движутся практически с той же скоростью, что и жидкость, т.е. скорость самопроизвольного всплытия равна нулю.

Но если размер пузырьков превысит величину:

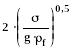(268)

то возникает специфический, так называемый, кильватерный эффект при котором всплывающий пузырёк увлекает за собой в своей кильватерной струе следующий пузырёк и т.д. В результате, получает значения лежащие существенно выше приведённой кривой (точки отмечены звёздочкой), и носящие название точек захлёбывания. При этом, в формуле (267) будет меньше 1.

В результате, смесь сильно турбулизируется и течение приобретает неустановившийся характер; а пузырьки начинают интенсивно агломерироваться и сливаться.

При этом, надо иметь в виду, что кроме увлекающей силы жидкости и силы самопроизвольного всплытия на пузырёк могут действовать и другие силы, например, под действием вибраций возникает опускающая сила, противодействующая подъёмной. И если она достаточно велика, то пузырёк перестает подниматься и лишь колеблется около положения равновесия и даже способен опускаться.

Перейдём непосредственно к гидравлическим расчетам.

Если смесь ведёт себя как однофазная ньютоновская жидкость (разумеется, если сама жидкость не является неньютоновской), подчиняющейся обычным формулам Дарси – Вейсбаха и Лейбензона, за той лишь особенностью, что в турбулентной области:

(269)

а в ламинарной:

(270)

При больших объёмных газосодержаниях смесь быстро приобретает свойства неньютоновской жидкости, а, затем, и вязкоупругой жидкости, что требует соответствующего решения вышерассмотренными методами.

Если же реология смеси неизвестна или не ясен вид течения, то гидравлический расчет для пузырькового режима можно осуществить с помощью так называемого общего подхода, согласно которого для изотермического течения:

(271)

где: - потери давления, связанные с относительным движением фаз;

- потери давления, связанные с трением;

- потери давления, связанные с действием силы тяжести.

(272)

(273)

где: - величина без названия, находящаяся по соотношению:

(274)

где: - приведённая скорость газа, определяемая как:

(275)

- приведённая скорость жидкости, определяемая как:

(276)

- безразмерная величина, находящаяся по соотношению:

(277)

(278)

Поскольку в общем случае при осуществлении гидравлических расчетов более правильно пользоваться не расходным газосодержанием , а его истинным значением . Однако, его нахождение для пузырькового режима течения настолько сложно, а разница в итоговых результатах настолько незначительна, что рассмотрением этого вопроса мы принебрегём.

Практическое занятие № 11

Пробковый режим

Он характеризуется последовательным прохождением по трубопроводу одиночных больших пузырей, занимающих почти всё его сечение и отделённых друг от друга жидкостными пробками с сохранением на стенках жидкостной плёнки.

Для данного режима течения истинное газосодержание можно рассчитать достаточно легко по формулам А.И.Гукова:

Для восходящих труб:

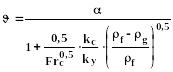(279)

Для нисходящих труб:

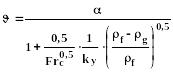(280)

где: - коэффициент, учитывающий влияние газонасыщенной среды на относительное движение фаз;

- коэффициент, учитывающий устойчивость газовых включений в газожидкостном потоке.

(281)

(282)

где: - расходное объёмное газосодержание при среднем давлении .

Практически не существует нижней границы газосодержания меньше которой было бы невозможно существование пробкового режима.

Если в горизонтальных и восходящих трубах затормозить движение пузырей, то они начнут дробиться на более мелкие (примерно в 2 – 3 диаметра трубопровода), но к смене режима это не приведёт.

А вот если разогнать смесь до очень высоких скоростей, пузыри начинают дробиться со сменой режима течения на пузырьковый. Этот процесс начинается если:

> (283)

В нисходящих трубах возможно возникновение противоточного движения, т.е.случая когда жидкость не в силах увлечь пузыри, стремящиеся всплыть. Этот случай носит название захлёбывания и является переходным к кольцнвому режиму течения.

О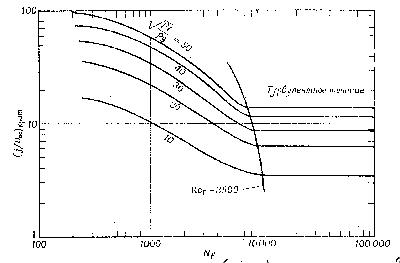 ценить вероятность захлёбывания можно с помощью графика Порто (рис.32):

Рис.32. График Порто.

Если:

> (284)

то захлёбывание становится неизбежным.

Безразмерный комплекс определяется соотношением:

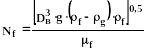(285)

Неплохие результаты даёт так же соотношение Уоллиса, согласно которого захлёбывание наступает, если:

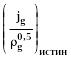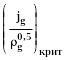< (286)

где:

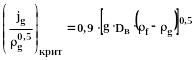(287)

В общем случае:

(288)

где: - падение давления в жидкой пробке – оно может быть определено по обычной методике для однофазной жидкости;

- падение давления на концах газового пузыря – оно может быть определено через основные параметры состояния;

- падение давления вдоль пузыря – оно обычно ~0, т.к.плотность и вязкость газа намного меньше чем жидкости.

А.И.Гудковым так же была сделана попытка подойти к определению потерь давления в общем случае т.е.без рассмотрения конкретных особенностей пробкового режима.

Им было предложено соотношение:

(289)

где: расходная плотность может быть определена из соотношения:

(290)

Истинная плотность может быть определена из соотношения:

(291)

Приведённый коэффициент сопротивления, учитывающий относительное движение фаз, предлагается определять по формулам:

Для восходящих потоков:

(292)

для нисходящих потоков:

(293)

Коэффициент гидравлического сопротивления предлагается находить полагая, что по трубопроводу движется только жидкость с тем же массовым расходом.

Разумеется, такой общий подход не может обеспечить требуемую точность и может применяться лишь для оценочных расчетов.

Более точные расчеты базируются на рассмотрении конкретных особенностей пробкового режима.

Вертикальное пробковое течение

Начнём с простейшего случая – жидкость неподвижна.

Если вязкостью газа в пузыре принебречь, то его поведение определяется 4 факторами: подъёмной силой, инерцией жидкости, вязкостью жидкости и поверхностным натяжением.

Ещё упростим задачу:

1. Пусть преобладающее влияние оказывают силы инерции, т.е. другими силами можно принебречь. Тогда:

(294)

где:

2. Пусть преобладающее влияние оказывают вязкостные свойства жидкости, тогда:

(295)

где:

3. Пусть преобладающее влияние оказывают силы поверхностного натяжения (т.е.пузырёк неподвижен). Тогда:

(296)

Граничные условия для остановки пузырька оцениваются с помощью параметра Этвешта или параметра Бонда :

(297)

(298)

Пузырёк перестаёт самопроизвольно всплывать, если:

< (299)

или:

< (300)

Если неизвестна природа преобладающих сил, то пользуются следующими соотношениями:

Если: >300 и >100, то это область преобладающего влияния инерционных сил.

Если: < 2 и >100, то это область преобладающего влияния сил вязкости.

Если:

(301)

и <3,37, то это область преобладающего влияния сил поверхностного натяжения.

где:

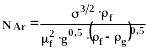(302)

Во всех остальных случаях действует совокупность всех сил, без преобладающего влияния одной из них. Расчет в этом случае настолько усложняется, что рассмотрение этого вопроса выходит за рамки курса.

Поскольку жидкость неподвижна, скорость дрейфа пузыря будет постоянна и может быть определена по соотношению:

(303)

где:

(304)

В общем случае при неподвижной жидкости:

(305)

Перейдём к рассмотрению более сложного случая когда жидкость движется. При этом, скорость дрейфа пузыря уже не является постоянной величиной, ибо на неё оказывает влияние профиль скорости жидкости, а он по сечению переменен. В целом, жидкость может двигаться быстрее пузыря, с равной ему скоростью и медленнее пузыря; хотя представит себе, например, более медленное движение жидкости в нисходящих трубахх достаточно сложно.

Итак, если жидкость движется:

(306)

Горизонтальное пробковое течение

В условиях горизонтального течения скорость дрейфа, обусловленная действием подъёмных сил, равна нулю. Поэтому параметр теряет смысл. Однако, средняя скорость движения пузырей отличается от средней скорости жидкости, причём, плёнка жидкости на стенке практически неподвижна. Обычно, > и < , т.е. скорость газовой пробки больше средней скорости смеси, а скорость жидкости меньше средней скорости смеси. И только при очень малых средних скоростях газовая пробка и жидкость движутся с одинаковой скоростью. Обычно это соблюдается до , после чего скорость газового пузыря становится равной:

(307)

Перепад давления в этом случае может быть оценён по одной из следующих формул:

(308)

где: - длина одной жидкостной пробки;

- длина одной газовой пробки.

(309)

где: - объём одного газового пузыря.

(310)

где: - площадь поперечного сечения трубопровода;

- площадь поперечного сечения газового пузыря.

Истинное газосодержание в этом случае может быть оценено соотношением:

(311)

И, наконец, последняя используемая зависимость для нахождения перепада давления:

(312)

Наклонное пробковое течение

Поведение газожидкостной смеси в наклонных трубах аналогично её поведению в вертикальных трубах, причём, скорость самопроизвольного подъёма газового пузыря в наклонных трубах всегда выше, чем в вертикальных. Даже, если угол отклонения от вертикали всего 2 – 3⁰.

О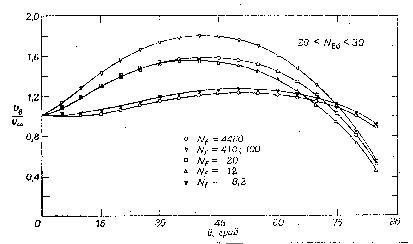 ценить эту самопроизвольную скорость ( ) можно с помощью следующих графиков (рис.39-42):

Рис.39. Зависимость самопроизвольной скорости от угла наклона трубопровода

Р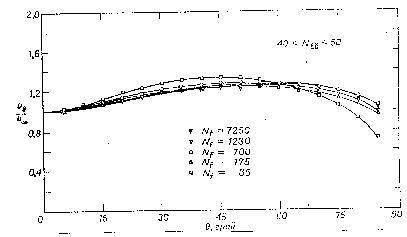 ис.40. Зависимость самопроизвольной скорости от угла наклона трубопровода.

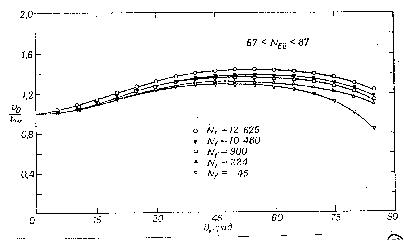
Рис.41. Зависимость самопроизвольной скорости от угла наклона трубопровода.

Р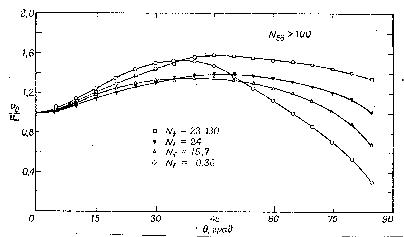 ис.42. Зависимость самопроизвольной скорости от угла наклона трубопровода

Пульсация давления.

Все приведённые выше уравнения для определения градиента давления дают лишь его средние значения. Но в действительности же давление вдоль газового пузыря постоянно, поэтому действительное распределение давления по длине трубопровода сопровождается его пульсациями (рис.37):

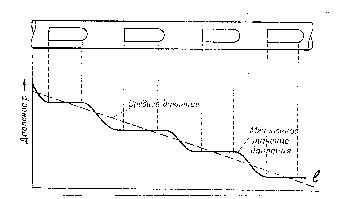
Рис.43. Схема пульсации давления при пробковом режиме

Практическое занятие № 12

Кольцевой режим

При кольцевом режиме течения по стенке трубы движется жидкость в виде плёнки (кольца), а в центральной части трубопровода – газ, несущий капли жидкости ( ядро потока). Если в газовом ядре распределено значительное число унесённых капель жидкости, то это переходная область к дисперсному режиму.

Горизонтальные трубы

Границы кольцевого течения для горизонтальных труб до сих пор точно не определены, хотя понятно, что чем больше расход газа, тем интенсивнее унос капель, а чем больше расход жидкости, тем более вероятен переход к пробковому или пузырьковому режиму.

Границу между пробковым и кольцевым течением можно примерно описать с помощью соотношения Бейкера:

(313)

Величина не имеет не только специального названия. Но и физического смысла, хотя и характеризует соотношение сил инерции газовой фазы и сил тяжести газа.

Переход от пробкового режима к кольцевому осуществляется при достижении величины 0,25 – 1,0.

Граница между кольцевым и дисперсным течением может быть оценена с помощью так называемой критической скорости газа , определяемой из соотношения:

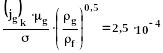(314)

Как только достигнет значения - обычно десятки метров в секунду- при котором будет соблюдаться данное равенство, произойдёт смена режима течения.

Если скорость газа невелика, поверхность жидкостной плёнки гладкая и величина коэффициента трения приблизительно такая же, что и в гладких трубах с однофазной жидкостью. Это позволяет для нахождения перепада давления использовать обычные формулы Дарси – Вейсхбаха и Лейбензона.

Если скорость газа превысит некую критическую величину, то начнётся волновое движение плёнки и величина коэффициента трения резко возрастёт вплоть до максимального значения.

В этом случае, уравнение для нахождения перепада давления имеет вид:

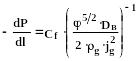(315)

При ещё больших скоростях газа происходит срыв верхушек волн и унос капель, приводящий к увеличению плотности ядра потока. При этом, коэффициент трения ещё более возрастает до тех пор пока почти вся жидкость не переёдёт в газовое ядро. В этом случае:

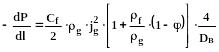(316)

Коэффициент трения, входящий в вышеприведённые формулы, можно определить по следующим соотношениям:

(317)

(318)

где: - толщина жидкостной плёнки на стенке трубопровода.

Истинное газосодержание (а, значит, и относительную скорость газа) можно оценить с помощью параметра Мартинелли :

(319)

Величина показывает, в какой степени поведение двухфазной смеси ближе к жидкости, чем к газу.

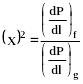(320)

т.е. это отношение гипотетического падения давления в трубопроводе если бы по нему двигалась только жидкость с тем же массовым расходом к гипотетическому падению давления в трубопроводе если бы по нему двигался только газ с тем же массовым расходом.

Вертикальные и наклонные трубы

1. Жидкость стекает вниз, газ поднимается вверх

Подобная ситуация возможна при незначительных скоростях газа. В этом случае количество стекающей жидкости ( ) можно оценить соотношением:

(321)

При этом, толщину жидкостной плёнки ( ) можно найти через относительную безразмерную толщину ( ), вычисляемую по соотношению:

(321)

Тогда ( ) можно найти с помощью одной из двух следующих формул:

(322)

или:

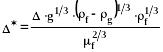(323)

С увеличением количества газа (при том же количестве жидкости) на её поверхности возникают всё большие волны, количество стекающей жидкости уменьшается и, наконец, жидкость начинает двигаться в одном направлении с газом. Момент перемены направления движения жидкости носит название захлёбывания, но в отличии от других видов течения не ведёт к смене способа течения. Захлёбывание наступает при достижении равенства:

(324)

где: - находится аналогично уже известной нам :

(325)

В случае противоточного движения перепад давления можно найти с помощью одного из двух следующих соотношений:

(326)

или:

(327)

где: ( ) представляет собой следующее соотношение:

(328)

- изменяется в диапазоне от 2,5 до 3,5

Если жидкость вязкая, то условие захлёбывания несколько иное:

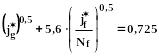(329)

да и перепад давления будет определяться из следующего иного соотношения:

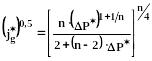(330)

2. Жидкость и газ движутся вниз

В этом случае количество стекающей жидкости можно оценить тем же соотношением (321), а величину определить с помощью графика (рис. 44).

Параметр , характеризующий величину касательных напряжений на поверхности жидкости, можно найти по уравнению:

Р ис.44. Номограмма для определения

(331)

3. Жидкость и газ движутся вверх

Данная ситуация возможна, если:

(332)

В этом случае перепад давления можно оценить несколькими способами:

а) Можно воспользоваться соотношением Миланского информационного центра научных исследований, согласно которого:

(333)

где: - удельный объём смеси

б) Для турбулентного течения жидкостного кольца возможно соотношение:

(334)

для ламинарного течения кольца жидкости возможно соотношение:

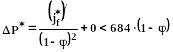(335)

где:

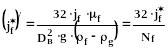(336)

в)

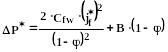(337)

где: коэффициент определяется по графику (рис.45):

Параметр - учитывает крутизну профиля касательных напряжений.

Если <1000, то = 0,684

Если 1000 < < 8000, то = 0,193^.

Если > 8000, то ~1

г) Наконец:

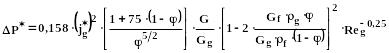(338)

Дисперсный режим

Основное отличие от пузырькового режима состоит в том, что у пузырькового течения основная часть сил инерции приходится на непрерывную фазу, поэтому пузырьки следуют за движущейся жидкостью почти совпадая с ней. У дисперсного течения основная часть сил инерции приходится на дискретную фазу, поэтому отличия в движении фаз существенно больше (жидкость в виде тумана в газе).

Р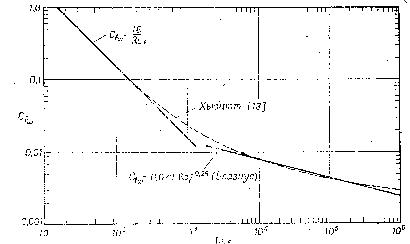 ис.45. График для определения коэффициента

Образование капель

1. Прокапывание жидкости через отверстия в движущийся газ. В этом случае размеры образующихся капель можно оценить соотношением:

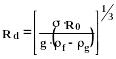(339)

где: - радиус отверстия

2. Конденсация паров на стенке. В этом случае размеры образующихся капель можно оценить соотношением:

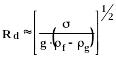(340)

3. Дробление газом струи жидкости. В этом случае размеры образующихся капель можно оценить соотношением:

(341)

4. Распыление жидкости. Сначала размер капель определяется конструкцией распыляющего устройства, затем поведение капель описывается критерием Вебера ( ):

(342)

Если <12, то образовавшиеся капли устойчивы и их размеры можно вычислить из соотношения:

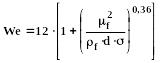(343)

Если >12, то образовавшиеся капли начинают дробиться. Их новые размеры можно оценить соотношением:

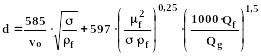(344)

где:

(345)

отношение начальных скоростей, причём: - в г/см³; - в мк; - в дин/см; - в дин^.с/см².

Если >>12, то размеры капель можно определить из соотношения:

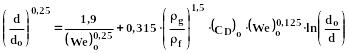(345)

где: индекс «о» относится к начальным условиям, а - некий коэффициент сопротивления, подбираемый опытным путём.

5. Унос. При малых скоростях газа его действие на плёнку жидкости незначительное.

С ростом относительной скорости газа в плёнке возникают возмущения, причём, в горизонтальных или наклонных трубах сила тяжести действует как восстанавливающая сила, затягивающая начало заметной волновой активности.

Первые волны представляют собой небольшую рябь, бегущую в направлении движения плёнки жидкости. С увеличением скорости газа растёт амплитуда этой ряби и вскоре появляются трёхмерные возмущения. Поверхность раздела фаз приобретает «насеченную» в поперечном направлении структуру.

При скорости газа примерно в два раза больше, чем для возникновения вышеописанных возмущений, появляются первые скатывающиеся волны, которые имеют значительно большую амплитуду и скорость. Чем предыдущие и как бы перекатываются через более равномерные волны малой амплитуды. Их фронт крутой, а между гребнями – протяженная область сравнительно спокойной жидкости.

При ещё большей скорости газа силы, действующие на верхушки гребней, становятся достаточными для того, чтобы сорвать с них капли жидкости, которые уносятся в газовый поток. Началу уноса обычно предшествует появление «белых барашков», бегущих по поверхности жидкостной плёнки.

Дальнейшее увеличение расхода газа приводит к росту уноса и уменьшению толшины жидкостной плёнки, в следствии потери массы.

Расход жидкости оказывает слабое влияние на переход от кольцевого к дисперсному режиму. Критическая скорость газа (начало уноса) слабо зависит от размеров трубопровода, его ориентации в пространстве и расхода жидкости.

Начало уноса определяется критерием Стина: :

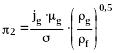(346)

Как только превысит величину 2,46^.10^-4 начинается унос.

Разумеется, что все диаметры, рассмотренные выше, средние. На самом деле капли имеют некое распределение по диаметру, которое лучше всего описывается функцией Нукиямы – Танасавы:

(347)

Обычно, и - целые числа, которым иногда можно придать физический смысл. и - нормирующие множители.

Как правили:

(348)

(349)

(350)

где: - это средний диаметр, рассчитанный по вышеприведённым формулам.

Все капли стремятся самопроизвольно осесть.

Если Re<1 капли подчиняются уравнению Адамара – Рябчинского и их максимальная скорость оседания определяется по формуле:

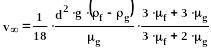(351)

Если Re>1000:

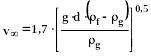(352)

Если капли не круглые:

(353)

Данный режим тоже может захлёбываться. Это происходит когда характеристическая скорость ( ) достигнет величины:

(354)

где:

(355)

Расчет потерь давления при данном режиме аналогичен определению потерь давления при движении смеси газов и жидкости с твёрдыми частицами и будет рассмотрен ниже в следующей главе.

Расслоенный и волновой режим

Расслоенная структура потока характеризуется наличием непрерывной газовой фазы в верхней части сечения горизонтальной трубы. Характерными особенностями расслоенного потока является относительно большая разница в скоростях фаз и полное отсутствие пульсаций давления. Расслоенная структура может наблюдаться только в горизонтальных и нисходящих трубопроводах, при этом, в горизонтальном трубопроводе скорость газовой фазы выше, чем жидкой, а в нисходящем трубопроводе, наоборот.

Волновая структура потока характеризуется наличием на поверхности раздела фаз волн. Если волны не достигают верхней образующей трубы, движение газо – жидкостной смеси происходит при очень малых пульсациях давления, но при высоких частотах. Если волны достигают верхней образующей трубы, происходит периодическое затормаживание потока в результате чего пульсация давления достигает весьма ощутимых величин.

Гидравлические расчеты для расслоенного и волнового течения аналогичны соответствующим расчетам для кольцевого течения и поэтому добавочно здесь не рассматриваются.

Эмульсионный режим

Эмульсионная структура потока (течение пены) встречается крайне редко и обладает всеми рассмотренными ранее свойствами вязко – упругих жидкостей и добавочно не рассматривается.

Практическое занятие № 13

Технические модели течения

Эти модели применяют независимо от конкретного способа течения смеси. Они более упрощены, зачастую базируются на эмпирических данных и гораздо менее точны, но очень удобны в практических расчетах.

Общепризнанные модели:

Трубопровод рассчитывают по участкам; каждый участок должен быть одного диаметра и иметь одинаковую шероховатость, а также одинаковые условия теплообмена с окружающей средой. Если перепад давления на любом участке превышает 5 % от начального давления, то его делят пополам. Каждое местное сопротивление считается отдельным участком.

Горизонтальные трубопроводы

Существует несколько методик расчета, описывающих данные модели. Их выбор осуществляется с помощью табл.1.

Таблица 1.

Выбор методик расчета потерь давления на трение

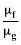
, кг/м2.с		Методика Расчета
До 100 Свыше 100 Независимо	Свыше 1000 Свыше 1000 До 1000	Локкарта – Мартинелли Чисхолма Фриделя

Методика Локкарта – Мартинелли:

В её основе лежит уравнение:

(356)

где: и - эмпирически определяемые поправочные коэффициенты;

и - потери давления на трение при движении по данному трубопроводу только жидкости или газа с теми же массовыми расходами.

(357)

(358)

где: - параметр Мартинелли;

- параметр двухфазности, определяемый по табл.2.

Таблица 2.

Определение параметра

		Параметр
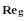
>2000 <2000 >2000 <2000	>2000 >2000 <2000 <2000	20 12 10 5

В области (и газ и жидкость движутся турбулентно) рекомендуется более точное соотношение:

(359)

В области ламинарного течения жидкости и турбулентного течения газа можно воспользоваться соотношением:

(360)

Параметр Мартинелли можно найти несколькими способами:

а) :

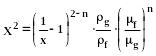(361)

где: - массовое расходное газосодержание;

- эмпирический показатель степени.

Если , то ;

Если < , то

Если < , то

Если > , то

б) С помощью универсальных зависимостей Верма:

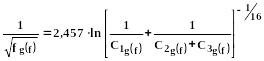(362)

где:

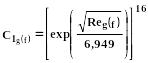(363)

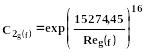(364)

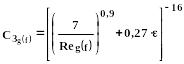(365)

где: - относительная шероховатость внутренней стенки трубы;

- коэффициент гидравлического сопротивления, связанный с коэффициентом гидравлического сопротивления ( ) следующим соотношением:

(366)

Ну, а зная - легко определить параметр Мартинелли:

(367)

в) С помощью универсальной зависимости Черчилла:

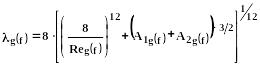(368)

где:

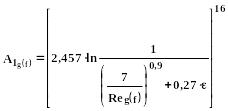(369)

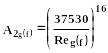(370)

Ну, а зная легко определить параметр Мартинелли.

Методика Чисхолма:

В основе её лежит уравнение:

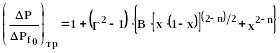(371)

где: - потери давления при движении по данному трубопроводу только жидкости с массовой скоростью равной массовой скорости всего двухфазного потока;

- параметр Чисхолма

для гладких труб:

(372)

для шероховатых труб:

(373)

Для гладких труб параметр определяют по табл. 3.

Таблица 3.

Определение параметра

	, кг/м2.с	Параметр
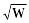
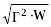
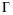
До 90 От 90 до 784 Свыше 784	До 500 От 500 до 1900 1900 и более До 600 Свыше 600 Независимо	4,8 2400/ 55/ 520/ 21/ 15000/

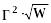
Для шероховатых труб:

(374)

где: - эмпирический коэффициент, подбираемый опытным путём.

Для шероховатых труб

Методика Фриделя:

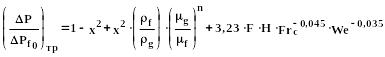(375)

где:

(376)

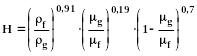(377)

Вертикальные и наклонные трубопроводы

При турбулентном течении применимы все вышеописанные методики, причём параметр двухфазности « » будет равным 26.

Разумеется, в этом случае к потерям давления на трение будут добавляться гидростатические перепады давления.

Расчеты, связанные с ламинарным течением, осуществляют по тем же самым формулам.

Отраслевые методики

В настоящее время имеется множество методик (ГрозНИИ, ВНИИГаз. ВНИИСПНнефть, ГИПРОВостокнефть и др.) гидравлического расчета нефтепроводов с газо – жидкостными потоками.

В качестве примера рассмотрим одну из методик, разработанной на кафедре ГиЭНиГМ Бородиным Ю.И.

(378)

где: и - удельные веса жидкой и газовой компоненты в условиях перекачки соответственно;

- угол наклона оси трубопровода к горизонту.

(379)

где: - приведённый коэффициент гидравлических сопротивлений.

(380)

(381)

где: - расходное газосодержание.

Разумеется, параметры - должны быть приведены к средним термодинамическим условиям перекачки (Р_ср и t_ср).

Параметры, входящие в основную формулу (378), рассчитываются по следующим зависимостям:

1. (382)

где: - удельный вес полностью дегазированной нефти (кгс/м³) в стандартных условиях;

- удельный вес газа, растворённого в нефти:

(383)

где: - удельный вес газа при н.у.;

- количество газа, растворённого в 1 м³ дегазированной нефти при Р_ср и Т_ср, нм³/м³

(384)

где: - газовый фактор однократного разгазирования, рассчитанный на 1 т дегазированной нефти, нм³/т;

- относительный удельный вес нефти в поверхностных условиях:

(385)

где: - удельный вес воды в поверхностных стандартных условиях;

- количество свободного газа, выделившегося из нефти при Р_ср и t_ср и приходящегося на 1 м³ дегазированной нефти.

Эта величина определяется по эмпирической формуле, полученной институтом ГИПРОВостокнефть:

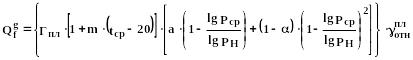(386)

где: и - подставляются в кГс/см²;

- газовый фактор однократного разгазирования, рассчитанный на 1 т пластовой нефти, нм³/т;

(387)

где: - относительный удельный вес газа при однократном разгазировании нефти:

(388)

где: - удельный вес воздуха в тех же условиях.

(389)

(390)

- относительный удельный вес нефти в пластовых условиях:

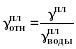(391)

где: - удельный вес нефти в пластовых условиях;

- удельный вес воды в пластовых условиях;

- давление насыщения нефти газом, ата;

- объёмный коэффициент учитывающий увеличение объёма нефти за счет растворенного в ней газа, определяется по номограмме (рис. 46).

Р ис.46. Номограмма для определения объёмного коэффициента

2.

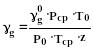(392)

где: =1,033 ата;

=273 К;

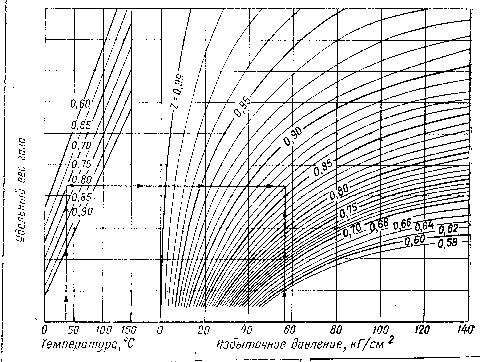
- коэффициент сверхсжимаемости, определяемый по рис.47:

Рис.47.Номограмма для определения коэффициента сверхсжимаемости

3. Истинное газосодержание потока ( ) определяется по формуле:

(393)

Данная формула справедлива в интервале:

0 < < 0,922

0 < < 303,7

При этом, начиная с

4. - может быть определена по любой из известных формул. При этом, для всей области турбулентного режима может быть рекомендована формула Альтшуля:

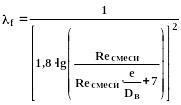(394)

4. Приведённый коэффициент гидравлического сопротивления определяется по формуле:

(395)

Формула справедлива в те же диапазонах и , что и формула для вычисления .

Если , то: и

4. Истинные средние скорости нефти и газа:

(396)

(397)

Практическое занятие № 14