О тчет по циклу лабораторных работ по дисциплине «Информатика» (2 семестр)

ФТПУ 7.1-21/1

 

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего профессионального образования

Томский политехнический университет

__________________________________________________________

Кафедра Информатики и проектирования систем

Отчеты по циклу лабораторных работ по дисциплине

«ИНФОРМАТИКА» (2 семестр)

Выполнил: ст-т гр. 2212 Грибачев В.О.

Принял: доц. каф. ИПС Хамухин А.А.

Томск - 2006

Оглавление

Оглавление 2

Отчёт по лабораторной работе №1 “Интерполяция и экстраполяция”. 3

Вывод: 6

Отчёт по лабораторной работе №2 “Аппроксимация ”. 7

Отчёт по лабораторной работе №3 “ Численное интегрирование ”. 15

Вывод: 18

Отчёт по лабораторной работе №4 “Поиск особых точек”. 19

Вывод: 24

Отчёт по лабораторной работе №5 “Базы данных ”. 25

Вывод: 29

Отчёт по лабораторной работе №1 “Интерполяция и экстраполяция”.

Цель работы:

научиться применять формулы полиномиальной и сплайн-интерполяции для восстановления отсутствующих (дефектных) значений в массивах экспериментальных данных.

Ход работы:

1. В соответствии с пунктами 1-4 создаю файл в Microsoft Excel. Выбираю номер дефектной точки и количество точек в массиве из своего индивидуального задания.

№ варианта (уровень А)	29
Количество точек в исходном ряде данных	20
Номер дефектной точки	15

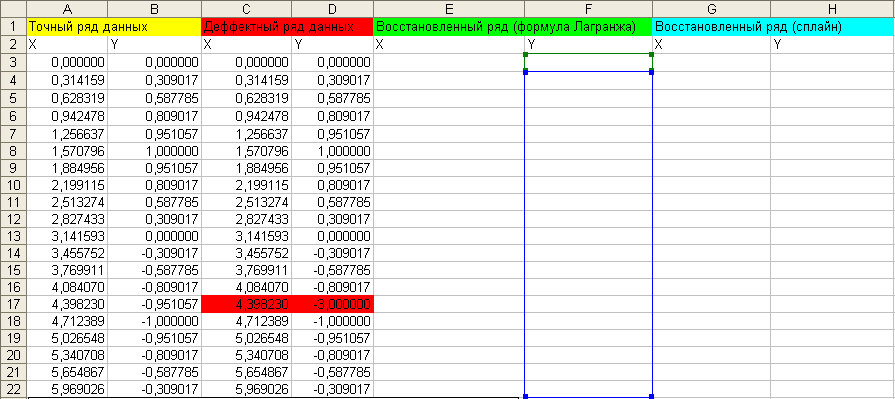
2. Записываю программы для расчета по формуле Лагранжа, сплайн - интерполяции и очистки результатов:

S = 0

For i = 1 To N

p = 1

For j = 1 To N

If j <> i And j <> Nz Then p = p * ((x(Nz) - x(j)) / (x(i) - x(j)))

Next j

If i <> Nz Then S = S + y(i) * p

Next i

y(Nz) = S

'Пуск сплайна

S = 0

For i = Nz - Nspline To Nz + Nspline

p = 1

For j = Nz - Nspline To Nz + Nspline

If j <> i And j <> Nz Then p = p * ((z - x(j)) / (x(i) - x(j)))

Next j

If i <> Nz Then S = S + y(i) * p

Next i

y(Nz) = S

Результаты:

3. Изменяю порядок сплайна и проверяю значения погрешности:

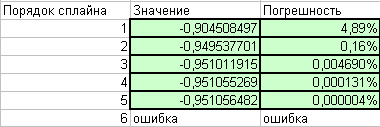
4. В соответствии с пунктом 9 по заданному преподавателем количеству точек создаю ряды данных для экстраполяции:

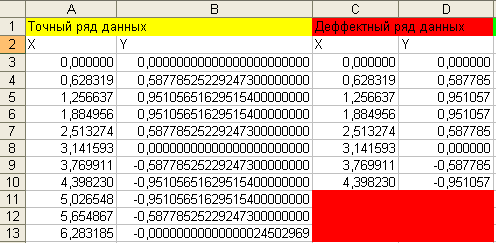
5. Пишу программы для всех кнопок.

Результаты:

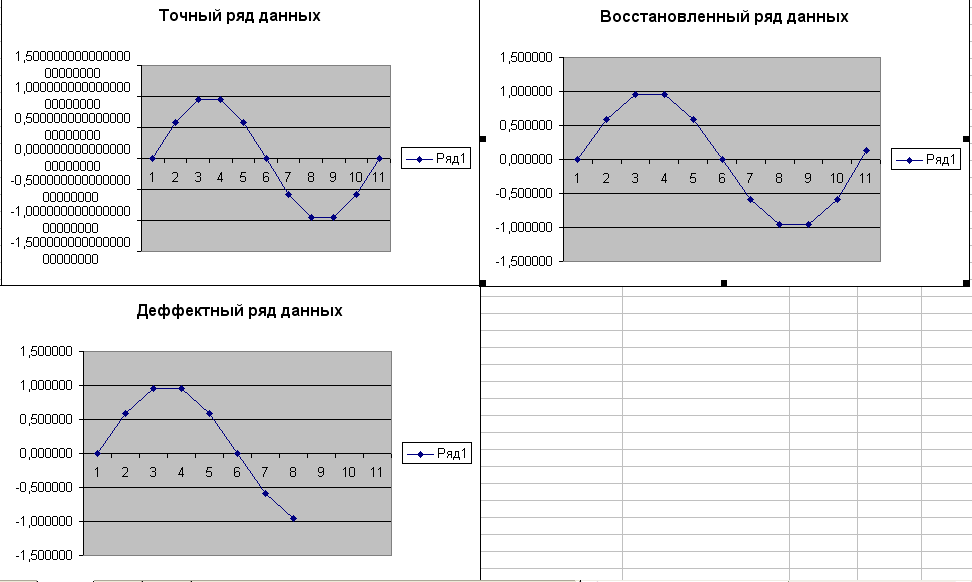
Количество точных точек	11
Восстановить точки	12, 13,14

S = 0

For i = k To N

p = 1

For j = k To N

If j <> i And j <> nz Then p = p * ((x(nz) - x(j)) / (x(i) - x(j)))

Next j

If i <> nz Then S = S + Y(i) * p

Next i

Y(nz) = S

Результаты:

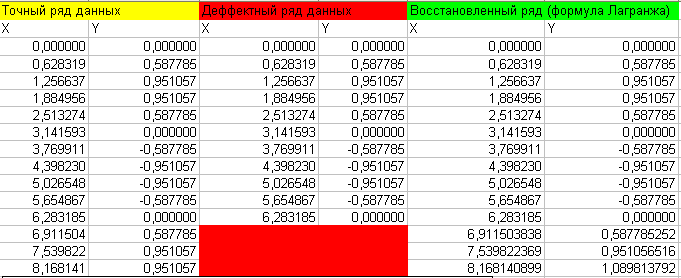
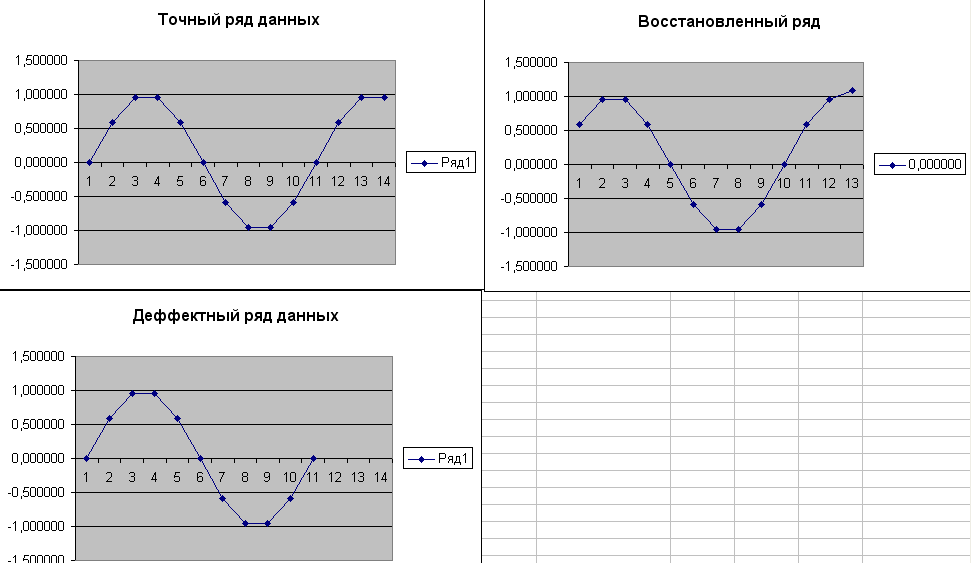
Вывод:

1. Относительная погрешность при использовании метода Лагранжа достаточно мала, значит, точность данного метода очень высока. При увеличении числа исходных точек погрешность снижается.

2. В методе сплайн – интерполяции погрешность достаточно высока, при использовании сплайна первого порядка. С увеличением порядка растет и точность вычислений, то есть погрешность уменьшается, но это происходит до тех пор, пока сумма (разность) номера дефектной точки и порядка сплайна не станет либо отрицательным числом, либо превзойдет количество заданных точек.

3. Относительная погрешность при использовании метода экстраполяции возрастает с увеличением разности между номером дефектной точки и последним известным значением. При увеличении числа исходных точек погрешность снижается.

4. Наиболее практичным методом является: способ Лагранжа для восстановления одной точки. Метод сплайн-интерполяции эффективен, если использовать порядок сплайна больший, чем 1. Метод экстраполяции подходит для восстановления нескольких дефектных точек, если массив данных точек велик (чем больше ток дано, тем больше мы можем восстановить с малой погрешностью).

 Оглавление