2.Решение нелинейного уравнения
2.1.Общие сведения
Уравнение типа F(x)=0 или x=f(x) называется нелинейным. Решить уравнение это значит найти такое х, при котором уравнение превращается в тождество, в общем случае уравнение может иметь 0; 1; 2;…∞ корней. Рассмотренные ниже численные методы решения нелинейных уравнений позволяют находить один корень на заданном интервале [a,b]. При этом на интервале должен существовать только один корень.
Решение уравнения складывается из двух этапов:
1. отделения корня, т. е. грубой оценки значения корня, которое используется в качестве начального приближения при его последующем уточнении;
2. уточнения корня, т.е. доведения его численного значения до заданной степени точности.
Для определения корня (определения начального приближения) следует пользоваться графическим методом.
2.2.Исходные данные
Нелинейно уравнение имеет вид:
х = х2 – 1
2.3.Решение методом половинного деления
При решении нелинейного уравнения методом половинного деления задаётся интервал [a,b], на котором существует только одно решение, и желаемая точность ε. Затем определяется середина интервала с=(а+b)/2 и проверяется условие F(a)∙F(c)<0. Если указанное условие выполняется, то правую границу интервала b переносим в среднюю точку с (b=с). Если условие не выполняется, то в среднюю точку переносим левую границу (а=с). Деление отрезка пополам продолжается пока |b−а| >ε.
2.4.Алгоритм решения
2.5.Программа решения
2.6.Результат работы программы
Корень уравнения х = х2 – 1 на отрезке [0;2] х=1.618
2.7.Проверка работы программы
1.618=1.6182−1=2.617924−1=1.617924
2.8.График функции y(x)=x2–x–1
3.Численное интегрирование
3.1.Общие сведения
Определённым
интегралом функции f(x),
взятом в интервале от a
до b,
называется предел, к которому стремится
интегральная сумма
Δxi
при
стремлении всех промежутков ∆xi
к нулю
=
.
При приближённом вычислении определённого интеграла шаг интегрирования h=∆x выбирается конечным:
=
≈
,
Где Ii – элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближённые формулы для вычисления интеграла методом прямоугольников.
3.2.Исходные данные
Численное интегрирование вида:
3.3.Решение по правилу прямоугольников
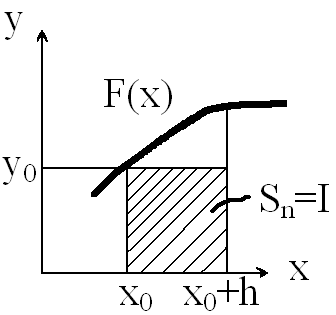
Заменяем график функции F(x) горизонтальной линией (линии нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника
I
=
≈
∙h,
где
h
– шаг интегрирования, y0
– значение функции в точке x=x0y(x0)=y0.
3.4.Алгоритм решения
3.5.Программа решения
3.6.Результат работы программы
S=172.026
3.7.Проверка работы программы
4.ОПИСАНИЕ ПРОГРАММЫ MathCad
4.1.Назначение
Mathcad является математическим редактором, позволяющим проводить разнообразные научные и инженерные расчёты, начиная от элементарной арифметики и заканчивая сложными реализациями численных методов. Пользователи Mathcad – это студенты, учёные, инженеры, разнообразные технические специалисты. Благодаря простоте применения, наглядности математических действий, обширной библиотеке встроенных функций и численных методов, возможности символьных вычислений, а также превосходному аппарату представления результатов (графики самых разных типов, мощных средств подготовки печатных документов и Web-страниц), Mathcad стал наиболее популярным математическим приложением.
В состав Mathcad входят несколько интегрированных между собой компонентов – это мощый текстовы редактор для ввода и редактирования как текста, так и формул, вычислительный процессор – для проведения расчётов согласно введённым формулам и символьный процессор, являющийся, по сути, системой искусственного интелекта. Сочетание этих компонентов создаёт удобную вычислительную среду для разнообразных математических расчётов и, одновременно, документирования результатов работы.