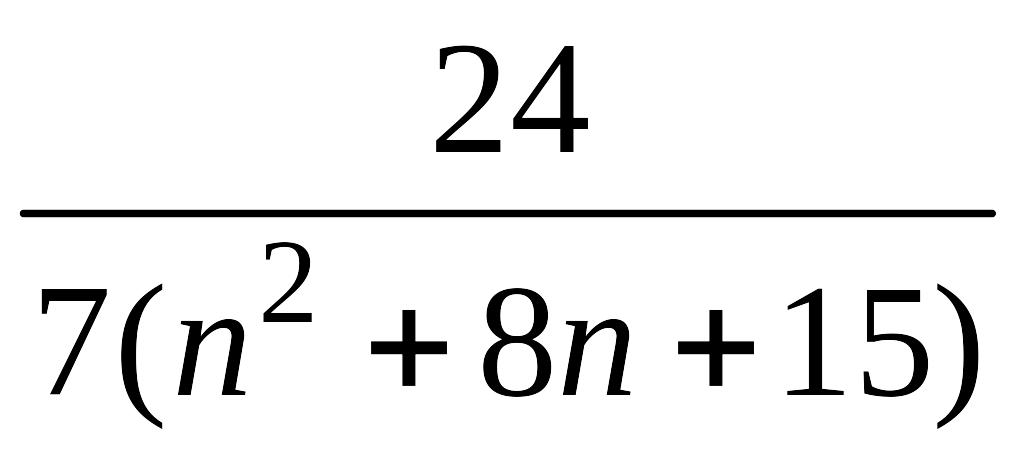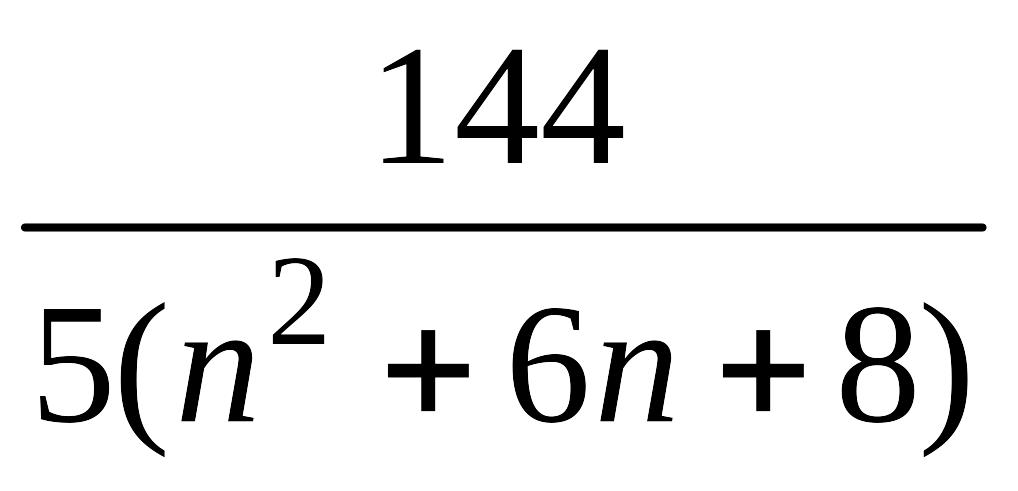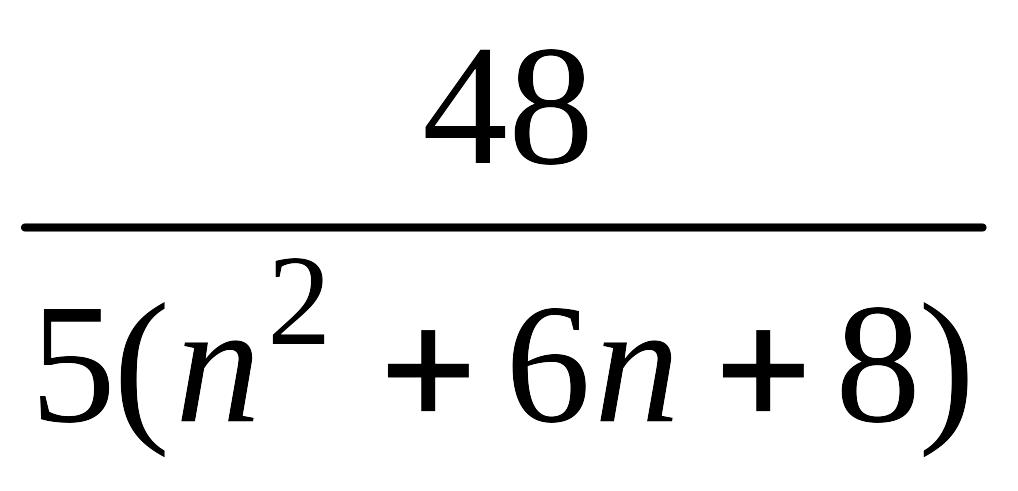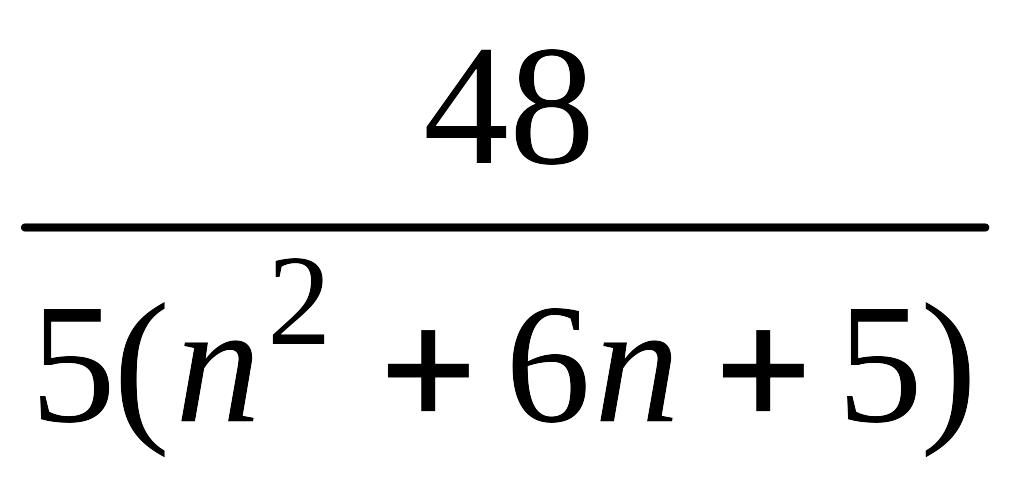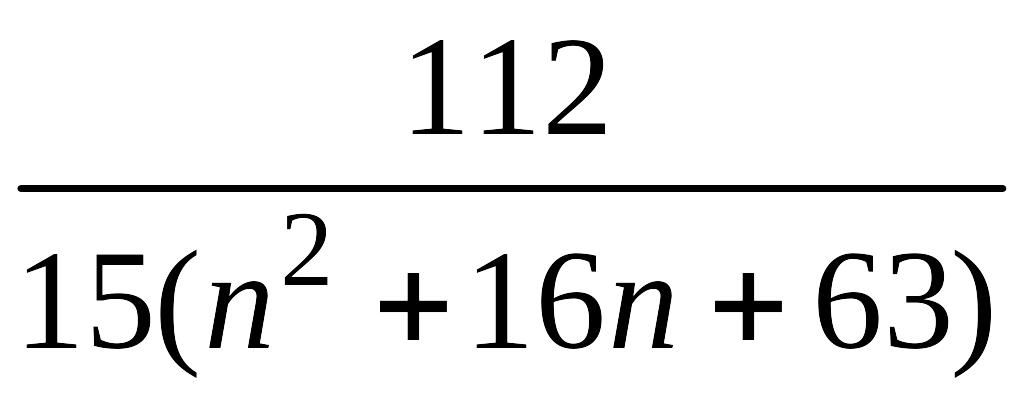Лабораторна робота №1 теорія похибок і машинна арифметика
Теоретичний матеріал до даної теми міститься в [1, розділ 1]. Варіанти до задач наведені в ДОДАТКУ 1.A. Приклад оформлення звіту лабораторної роботи наведений в ДОДАТКУ 1.B.
Задача
1.1. Дано
ряд
.
Знайти суму ряду аналітично. Обчислити
значення часткових сум ряду
і знайти величину похибки при значеннях
=
,
,
,
,
.
ПОРЯДОК РОЗВ’ЯЗКУ ЗАДАЧІ
1. Знайти суму ряду S аналітично як границю часткових сум ряду (див. ДОДАТОК 1.B).
2.
Використовуючи функцію
(
)
=
,
обчислити значення часткових сум ряду
при зазначених значеннях
.
3.
Для кожного
обчислити величину абсолютної похибки
і визначити кількість правильних цифр
в.
4. Подати результати у вигляді гістограми.
Задача
1.2. Дана
матриця A
=
.
У кожний із діагональних елементів
матриці A
по черзі внести похибку в 1%. Як змінився
визначник матриці А?
Указати кількість правильних цифр і
обчислити величину відносної похибки
визначника в кожнім випадку.
Задача
1.3. Для
заданої матриці A
знайти обернену матрицю (якщо це можливо).
Потім в елемент
внести похибку в 10% і знову знайти
обернену матрицю. Пояснити отримані
результати.
Задача 1.4. Знайти ранг заданої матриці A. Потім внести похибку в 0.1%: а) в елемент ; b) в усі елементи матриці і знову знайти ранг. Пояснити отримані результати.
Задача
1.5.
Дано квадратне рівняння
.
Передбачається, що один із коефіцієнтів
рівняння (в індивідуальному варіанті
позначений *) отриманий у результаті
округлення. Зробити теоретичну оцінку
похибок коренів у залежності від похибки
коефіцієнта. Обчислити корені рівняння
при декількох різних значеннях коефіцієнта
в межах заданої точності. Порівняти
отримані результати.
Задача 1.6. Для пакета MATHCAD знайти значення машинного нуля, машинної нескінченності, машинного епсилон (див. ДОДАТОК 1.B).
Задача 1.7. Обчислити значення машинного нуля, машинної нескінченності, машинного епсилон у режимах одинарної , подвійної й розширеної точності на двох алгоритмічних мовах. Порівняти результати.
Задача 1.8. Скласти програму, що моделює обчислення на ЕОМ з обмеженою розрядністю m. Розв’язати задачу 1.1 для випадку =10000, використовуючи цю програму. Побудувати графік залежності похибки від кількості розрядів m=4,5,…8.
Задача 1.9. Для матриці A вирішити питання про існування оберненої матриці в наступних випадках:
1) елементи матриці задані точно;
2)
елементи матриці задані приблизно з
відносною похибкою a)
=%
і b)
=
%.
Знайти відносну похибку результату.
ВКАЗІВКА. Див. ДОДАТОК 1.С.
Задача
1.10. Три
вектори
,
,
задані своїми координатами в базисі i
, j , k . Що
можна сказати про компланарності цих
векторів, якщо: 1) координати векторів
задані точно;
2) координати векторів задані приблизно з відносною похибкою: а) = % ; б) =%.
ВКАЗІВКА. Див. ДОДАТОК 1.С.
Додаток 1.A.
Схема варіантів до лабораторної роботи 1
N |
Виконувані задачі |
N |
Виконувані задачі |
1 |
1.1.1, 1.2.1, 1.7, 1.6, 1.10.1 |
16 |
1.1.16, 1.5.4, 1.7, 1.6, 1.8 |
2 |
1.1.2, 1.3.1, 1,7, 1.6, 1.10.2 |
17 |
1.1.17, 1.2.5, 1.7, 1.6, 1.8 |
3 |
1.1.3, 1.4.1, 1.7, 1.6, 1.10.3 |
18 |
1.1.18, 1.3.5, 1.7, 1.6, 1.8 |
4 |
1.1.4, 1.5.1, 1.7 , 1.6, 1.10.4 |
19 |
1.1.19, 1.4.5, 1.7 , 1.6, 1.9.1 |
5 |
1.1.5, 1.2.2, 1.7, 1.6, 1.10.5 |
20 |
1.1.20, 1.5.5, 1.7, 1.6, 1.9.2 |
6 |
1.1.6, 1.3.2, 1.7, 1.6, 1.10.6 |
21 |
1.1.21, 1.2.6, 1.7, 1.6, 1.9.3 |
7 |
1.1.7, 1.4.2, 1.7, 1.6, 1.9.1 |
22 |
1.1.22, 1.3.6, 1.7, 1.6, 1.9.4 |
8 |
1.1.8, 1.5.2, 1.7, 1.6, 1.9.2 |
23 |
1.1.23, 1.4.6, 1.7, 1.6, 1.9.5 |
9 |
1.1.9, 1.2.3, 1.7, 1.6, 1.9.3 |
24 |
1.1.24, 1.5.6, 1.7, 1.6, 1.9.6 |
10 |
1.1.10, 1.3.3, 1.7, 1.6, 1.9.4 |
25 |
1.1.25, 1.2.1, 1.7, 1.6, 1.10.1 |
11 |
1.1.11, 1.4.3, 1.7, 1.6, 1.9.5 |
26 |
1.1.26, 1.3.1, 1.7, 1.6, 1.10.2 |
12 |
1.1.12, 1.5.3, 1.7, 1.6, 1.8 |
27 |
1.1.27, 1.4.1, 1.7, 1.6, 1.10.3 |
13 |
1.1.13, 1.2.4, 1.7, 1.6, 1.8 |
28 |
1.1.28, 1.5.1, 1.7, 1.6, 1.10.4 |
14 |
1.1.14, 1.3.4, 1.7, 1.6, 1.8 |
29 |
1.1.29, 1.2.2, 1.7, 1.6, 1.10.5 |
15 |
1.1.15, 1.4.4, 1.7, 1.6, 1.8 |
30 |
1.1.30, 1.3.2, 1.7, 1.6, 1.10.6 |
ВАРІАНТИ ЗАВДАНЬ ДО ЛАБОРАТОРНОЇ РОБОТИ 1
Таблиця до задачі 1.1
N |
|
N |
|
N |
|
1.1.1 |
|
1.1.11 |
|
1.1 21 |
|
1.1.2 |
|
1.1.12 |
|
1.1.22 |
|
1.1.3 |
|
1.1.13 |
|
1.1.23 |
|
1.1.4 |
|
1.1.14 |
|
1.1.24 |
|
1.1.5 |
|
1.1.15 |
|
1.1.25 |
|
1.1.6 |
|
1.1.16 |
|
1.1.26 |
|
1.1.7 |
|
1.1.17 |
|
1.1.27
|
|
1.1.8 |
|
1.1.18 |
|
1.1.28 |
|
1.1.9 |
|
1.1.19 |
|
1.1.29 |
|
1.1.10 |
|
1.1.20 |
|
1.1.30 |
|
Таблиця до задачі 1.2
N |
A |
N |
A |
N |
A |
1.2.1 |
3 2 2 33 28 24 360 320 270 |
1.2.2 |
30 34 19 314 354 200 2 8 13 |
1.2.3 |
1.3 1 13 3.4 1.4 23 5 3 1.5 |
1.2.4 |
9 5 6 17 9 11 7 4 5 |
1.2.5 |
-7 -7 -1 0 -2 -6 5 6 4 |
1.2.6 |
3 1 13 5 3 15 11 5 40 |
Таблиця до задачі 1.3
N |
A |
N |
A |
N |
A |
1.3.1 |
1 8 11 |
1.3.2 |
2 4.4 -2 1 2 -1 3 -5 0 |
1.3.3 |
3 5 3 9 15 9 6 7 2 |
1.3.4 |
32 2 4 5 -1 2 |
1.3.5 |
1.1 0.2 3 2.3 1.2 4 |
1.3.6 |
5 5.5 5.5 1 1 1 5 -1 2 |
Таблиця до задачі 1.4
N |
A |
N |
A |
N |
A |
1.4.1 |
1.1 0.1 0.8 1.6 1.3 -0.3 1.2 2.1 0.9 0.5 0.4 1.1 -0.4 -3.8 2 1.3 |
1.4.2 |
0.6 4.5 0.3 3 -2.4 -12 0.9 -7 1.2 9 0.6 6 -1.2 3 3.6 4 |
1.4.3 |
1.8 4 0 1.9 20.9 37 -25 19.2 0.5 3 5 1.1 10.6 16 -20 8.9 |
1.4.4 |
2 15 22 7 1 14.1 18.8 2.3 2 4 9 9 -0.4 2.5 2.1 -2.4 |
1.4.5 |
1.9 9 1.6 0.1 11.3 23 6.8 -3.7 0.5 10 1.1 1.1 0.9 -11 -0.6 -2.1 |
1.4.6 |
1.2 9 0.6 6 1.6 23 -7.2 9 2 4 9 9 2 37 -15 12 |
Таблиця до задачі 1.5
N |
Коефіцієнти |
N |
Коефіцієнти |
N |
Коефіцієнти |
1.5.1 |
b* = -39.6 c = -716.85 |
1.5.2 |
b = 27.4 c* = 187.65 |
1.5.3 |
b* = 37.4 c = 187.65 |
1.5.4 |
b = -30.9 c* = 238.7 |
1.5.5 |
b* = -3.29 c = 2.706 |
1.5.6 |
b = -3.29 c* = 2.706 |
Таблиця до задачі 1.9
N |
A |
|
|
N |
A |
|
|
1.9.1 |
31 27 22 32.2 28.2 24 36 32 27 |
0.1 |
0.4 |
1.9.2 |
30 34 19 31.4 35.4 20 24 28 13 |
0.05 |
0.1 |
1.9.3 |
3 1 13 13.4 11.4 23 5 3 15 |
0.05 |
0.1 |
1.9.4 |
9 5 6 13.5 9.5 11 8 4 5 |
0.1 |
0.5 |
1.9.5 |
-7 -8 -10 28.6 27.6 25 7 6 4 |
0.1 |
0.2 |
1.9.6 |
-3 -1 -13 26.8 22.4 46 5 3 15 |
0.1 |
0.1
|
Таблиця до задачі 1.10
N |
а1 |
а2 |
а3 |
|
|
1.10.1 |
( 10 , 15 , 1) |
( 0.7, 5.7, -9) |
( 11, 16, 2) |
0.05 |
0.1 |
1.10.2 |
(- 2 , - 5 , 13) |
(14.2 , 11.2 , 28) |
( 0, -3, 15) |
0.5 |
0.1 |
1.10.3 |
( 24, 28, 13) |
(21.1, 25.1, 10) |
( 18, 22, 7) |
0.05 |
0.01 |
1.10.4 |
( 9, 17, 1) |
(27, 35, -18) |
( 6, 14, 4) |
0.5 |
0.1 |
1.10.5 |
(14, 4, 17) |
(33.9, 23.9 , 38) |
( 13, 3, 16) |
0.05 |
0.1 |
1.10.6 |
( 9, 17, 1) |
(27, 35, -18) |
( 6, 14, 4) |
0.5 |
0.1 |