1. Вероятность события. Определение статистической вероятности события.

Эксперимент – любая процедура, в результате которой наблюдается то иное явление.

Элементарное событие (исход) – появление/не появление результата испытания.

Пространство элементарных событий – множество, каждому элементу которого соответствует один исход испытания.

Элементарные события должны обладать свойством полноты (указаны всевозможные исходы) и свойством несовместимости (при одноразовом проведении эксперимента наблюдаем только одно элементарное событие)

Событие – подмножество множества элементарных событий (случайное событие). Например, выпадение 8 очков на 2-х игровых костях.

Для обозначения события используют: А, В, С…

Два события называются совместными, если появление одного их них не исключает появление другого в одном испытании. Например, при бросании кубика: совместные А={появление 4} и B={появление четного числа очков}.

Два события несовместны, если появление одного исключает появление другого (бросание монеты, орел/решка).

Два события А и В противоположны, если в данном испытании они несовместны и одно из них обязательно происходит.

Событие А называется достоверным, если оно является единственно возможным исходом некоторого испытания.

Невозможным является событие, которое не может произойти в некотором испытании.

Операции над событиями аналогичны операциям над множествами.

Классическое определение вероятности:

Во многих случаях возможно перечислить все исходы некоторых испытаний.

Вероятностью события А называется отношение 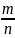, где m – число элементарных события благоприятствующих событию А, n – число всех элементарных событий.

Событие А называется благоприятствующим появлению события В, если наступление событие А влечет за собой наступление события В. (А-выпадет четное число; А₁-выпадет 2, А₂-выпадет 4, А₃-выпадет 6).

Свойства вероятностей:

1. Вероятность достоверного события равна единице,

2. Вероятность невозможного события равна нулю,

3. Вероятность случайного события 0<P(A)<1.

Статическое определение вероятности:

Есть вариант неравномерных событий. Если проведена серия из n опытов, в каждом из которых может появиться или не появиться событие А, то частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А к общему числу опытов.

Частота события и называется статической вероятностью.

m – число появления А, n – общее число опытов.

При небольшом числе опытов P’ носит случайный характер. Однако при увеличении числа опытов P’ теряет свой случайный характер приближаясь с незначительными колебаниями к некоторой средней величине (свойство устойчивости). Впервые математическая формулировка была дана Бернулли закон больших чисел).

Например, из 1000 выбранных деталей примерно 4 бракованных. Сколько бракованных примерно будет среди 2400: А={попалась бракованная}, P’(A)=4\1000=0,004; b=2400*0,004=9,6, т.е. около 10 бракованных деталей.

2. Случайные величины. Их основные характеристики.

Случайная величина – появляется в результате опыта. Может быть дискретной и непрерывной (число появления герба при 3-х бросаниях монет – дискретная, расстояние от точки попадания до центра мишени – непрерывная)

Случайная величина обозначается большими буквами: А,В,С; их значения: x,y,z.

Например, – случайная величина Х принимает значение х₁ с вероятностью

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Xi	X1	X2…	Xn
Pi	P1	P2…	Pn

- Ряд распределения случайно величины Х

Многоугольник распределения (если изображать графически)

Числовые характеристики случайных величин:

1. Характеристики положения

1. Математическое ожидание (среднее случайной величины).

Для дискретной случайной величины:

Xi	X1	X2…	Xn
Pi	P1	P2…	Pn

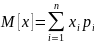
Математическим ожиданием случайной величины называется сумма произведений вех возможных значений случайной величины на вероятности этих значений.

Для непрерывной случайной величины:

Свойства: 1) Ели С не случайная величина, то M[C]=C; 2) С=const, M[CX]=C·M[X], 3)M[X+Y]=M[X]+M[Y], 4) M[ax+b]=a·M[x]+b, 5) M[x·y]=M[x]·M[y] если x,y независимые.

2. Мода (M_o)

Модой случайной величины называется наиболее вероятное ее значение. Строго говоря, это применимо к дискретным случайным величинам, а для непрерывных мода – это то значение, в котором плотность вероятности максимальна.

Если многоугольник распределения (кривая) имеет более одного максимума, то распределение называется полимодальным.

В общем случае, мода и математическое ожидание не совпадают, но если распределение является симметричным и модальным, то они равны и совпадают с центром симметрии.

3. Медиана (М_е)

Этой характеристикой пользуются для непрерывных случайных величин., но возможно и для дискретных.

Медиана случайной величины Х называется такое ее значение M_e, для которого P(x<M_e)=P(x>M_e), т.е. одинаково вероятна случайная величина меньше или больше М_e.

Геометрически медиана это абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

II. Моменты

1. Дисперсия

Это характеристики, которые описывают различные свойства распределения

Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания.

Для дискретной случайной величины:

Для непрерывной случайной величины:

Дисперсия – это характеристика разбросанности (рассеивания) значений случайной величины около ее математического ожидания.

Дисперсия имеет размерность квадрата. Для наглядной характеристики удобнее пользоваться величиной, размерность которой совпадает с размерностью самой случайной величины.

Эта характеристика называется среднее квадратическое отклонение:

Свойства дисперсии:

1)

3. Функция распределения и плотность распределения случайных величин.

Функция распределения

Характеристика «ряда распределения» не является универсальной (не подходит для непрерывной)

Д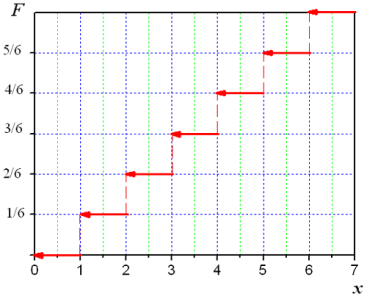 ля количественной характеристики распределения удобно пользоваться не вероятностью, что Х=х, а вероятностью того, что Х<x; х – некоторая переменная.

Эта функция называется функцией распределения случайной величины:

(она универсальна)

Свойства F(x):

1. Не убывающая, 2) F(-∞)=0, 3) F(+∞)=1.

Функция распределения любой дискретной величины – это разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков =1.

По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки меньше. Ступенчатая кривая становится более плавной и приближается к непрерывной величине.

Вероятность попадания случайной величины на заданный участок.

Рассмотрим (α; β). Какова вероятность попасть от α до β?

А={x< β}, B={x< α}, C={α≤x<β}

A=B+C, P(C)=P(A)-P(B). P(α≤x<β)=P(x< β)-P(x< α)= F(β)-F(α).

Плотность распределения

Характеристика вводится для непрерывных случайных величин. Задана случайная величина Х, с F(x) – непрерывная, дифференцируемая.

Вычислим вероятность попадания этой случайной величины на участок [x; x+Δx)

P(x≤X<x+Δx)=F(x+Δx)-F(x)

Замечание:

Свойства плотности:

1. f(x)≥0, т.к. F(x) неубывающая, 2)

4. Нормальный закон распределения и его параметры.

Нормальный закон распределения (закон Гаусса) играет очень важную роль в теории вероятности. Это наиболее часто встречающийся на практике закон распределения. Он является предельным законом, к которому приближаются все другие законы распределения. Можно доказать, что сумма большого числа независимых случайных величин, подчиненных каким угодно законам распределения приближенно подчиняется нормальному закону, и тем точнее, чем большее количество случайных величин.

Вероятность попадания случайной величины подчиненной нормальному закону на заданный участок:

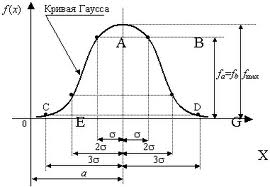
Правило трех сигм:

Для нормального распределения случайной величины с заданными a и σ, вероятность отклонения x-a больше чем на 3σ:

, т.е. с большой вероятностью значения нормального распределения случайной величины лежат в интервале (a-3σ; a+3σ)

5. Случайные функции. Их характеристики. Корреляционная функция. Опытное определение характеристик случайных функций (на математике не давали)

Случайный процесс описывается статистическими характеристиками, называемыми моментами. Важнейшими характеристиками случайного процесса являются его стационарность, эргодичность и спектр мощности.

Случайный процесс в его математическом описании Х(t) представляет собой функцию, которая отличается тем, что ее значения (действительные или комплексные) в произвольные моменты времени по координате t являются случайными. Строго с теоретических позиций, случайный процесс X(t) следует рассматривать как совокупность временных функций x_k(t), имеющих определенную общую статистическую закономерность. При регистрации случайного процесса на определенном временном интервале осуществляется фиксирование единичной реализации x_k(t) из бесчисленного числа возможных реализаций процесса X(t). Эта единичная реализация называется выборочной функцией случайного процесса X(t). Отдельная выборочная функция не характеризует процесс в целом, но при определенных условиях по ней могут быть выполнены оценки статистических характеристик процесса. Примеры выборочных функций модельного случайного процесса X(t) приведены на рис. 9.1.1. В дальнейшем при рассмотрении различных параметров и характеристик случайных процессов для сопровождающих примеров будем использовать данную модель процесса.

Рис. 9.1.1. Выборочные функции случайного процесса.

Функциональные характеристики случайного процесса.

Рис. 9.1.2. Сечения случайного процесса X(t).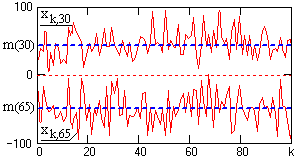

С практической точки зрения выборочная функция является результатом отдельного эксперимента, после которого данную реализацию x_k(t) можно считать детерминированной функцией. Сам случайный процесс в целом должен анализироваться с позиции бесконечной совокупности таких реализаций, образующих статистический ансамбль. Полной статистической характеристикой процесса является N-мерная плотность вероятностей р(x_n; t_n). Однако, как экспериментальное определение N-мерных плотностей вероятностей процессов, так и их использование в математическом анализе представляет значительные математические трудности. Поэтому на практике обычно ограничиваются одно- и двумерной плотностью вероятностей процессов.

Допустим, что случайный процесс X(t) задан ансамблем реализаций {x₁(t), x₂(t),… x_k(t),…}. В произвольный момент времени t₁ зафиксируем значения всех реализаций {x₁(t₁), x₂(t₁),… x_k(t₁),…}. Совокупность этих значений представляет собой случайную величину X(t₁) и является одномерным сечением случайного процесса X(t). Примеры сечений случайного процесса X(t) по 100 выборкам x_k(t) (рис. 9.1.1) в точках t₁ и t₂ приведены на рис. 9.1.2.

Одномерная функция распределения вероятностей F(x, t_i) определяет вероятность того, что в момент времени t_i значение случайной величины X(t_i) не превысит значения x:

F(x, t_i) = P{X(t_i)≤x}.

Очевидно, что в диапазоне значений вероятностей от 0 до 1 функция F(x, t) является неубывающей с предельными значениями F(-,t)=0 и F(,t)=1. При известной функции F(x,t) вероятность того, что значение X(t_i) в выборках будет попадать в определенный интервал значений [a, b] определяется выражением:

P{a<X(t_i)≤b} = F(b, t_i) – F(a, t_i).

Одномерная плотность распределения вероятностей p(x, t) случайного процесса Х(t) определяет вероятность того, что случайная величина x(t) лежит в интервале {x ≤ x(t) ≤ x+dx}. Она характеризует распределение вероятностей реализации случайной величины Х(t_i) в произвольный момент времени t_i и представляет собой производную от функции распределения вероятностей:

p(x, t_i) = dF(x, t_i)/dx. (9.1.1)

Моменты времени t_i являются сечениями случайного процесса X(t) по пространству возможных состояний и плотность вероятностей p(x, t_i) представляет собой плотность вероятностей случайных величин X(t_i) данных сечений. Произведение p(x, t_i)dx равно вероятности реализации случайной величины X(t_i) в бесконечно малом интервале dx в окрестности значения x, откуда следует, что плотность вероятностей также является неотрицательной величиной.

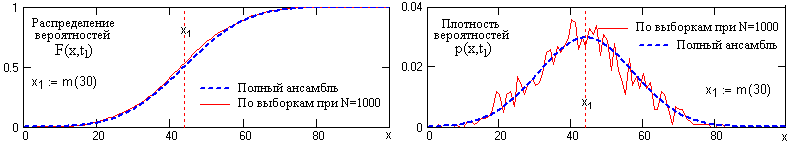
Рис. 9.1.3. Распределение вероятностей и плотность вероятностей сечения случайного процесса

На рис. 9.1.3 приведены примеры распределения вероятностей и плотности вероятностей сечения случайного процесса X(t) в точке t₁ (рис. 9.1.1). Функции вероятностей определены по N=1000 выборок дискретной модели случайного процесса и сопоставлены с теоретическими распределениями при N  .

При известной функции плотности вероятностей вероятность реализации значения X(t_i) в произвольном интервале значений [a, b] вычисляется по формуле:

P(a<X(t_i)≤b) = p(x,t_i) dx.

Функция плотности вероятностей должна быть нормирована к 1, т.к. случайная величина обязана принимать какое-либо значение из числа возможных, образующих полное пространство случайных величин:

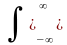p(x, t_i) dx =1.

Плотность распределения вероятностей, соответственно, определяет функцию распределения вероятностей:

F(x,t_i) =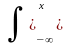 p(x, t_i) dx.

По известной плотности распределения вероятностей могут быть вычислены функции моментов случайного процесса, которые представляют собой математические ожидания соответствующих степеней (порядка) значений случайного процесса (начальные моменты) и значений флюктуационных составляющих процесса (центральные моменты, моменты относительно центров распределения случайных величин):

M{xⁿ(t)} = xⁿ(t) p(x, t) dx,

M₀{xⁿ(t)} = M{[x(t)-M{x(t)}]ⁿ} = [(x(t)- M{x(t)}]ⁿ p(x, t) dx,

Функции моментов являются основными статистическими характеристиками случайного процесса. Они представляют собой неслучайные функции, но полностью и однозначно определяют случайный процесс, как и плотность распределения вероятностей, при определенном количестве порядков в зависимости от характера процесса. Минимальное число порядков, которое полностью определяет гауссово распределение плотности вероятностей, равно 2.

В практике анализа случайных процессов используются, в основном, начальные моменты первого порядка и центральные моменты второго порядка.

Математическое ожидание является первым начальным моментом случайного процесса и представляет собой статистическое усреднение случайной величины X(t_i) в каком либо фиксированном сечении t_i случайного процесса. Соответственно, полная функция математического ожидания является теоретической оценкой среднего взвешенного значения случайного процесса по временной оси:

m_x(t)  M{Х(t)} = x p(x; t) dx, (9.1.2)

Математическое ожидание m_x(t) представляет собой неслучайную составляющую случайного процесса X(t). На рис. 9.1.1. и 9.1.2 неслучайные составляющие m(t) модели случайного процесса X(t) выделены пунктиром и соответствуют выборкам N  .

Второй начальный момент случайного процесса определяет его среднюю мощность:

w_x(t)  M{Х²(t)} = x² p(x; t) dx, (9.1.3)

Функция дисперсии случайного процесса. При анализе случайных процессов особый интерес представляет флуктуационная составляющая процесса, которая определяется разностью Х(t)-m_x(t). Функция дисперсии является теоретической оценкой среднего взвешенного значения разности Х(t)-m_x(t)², т.е. является вторым центральным моментом процесса, и определяет мощность его флуктуационной составляющей:

D_x(t) = M{[Х(t)-m_x(t)]²} = M{X²(t)} - m_x²(t) = [x_o(t)]² p(x; t) dx, (9.1.4)

где x_o(t) = x(t)-m_x(t).

Функция среднего квадратического отклонения (standard deviation) служит амплитудной мерой разброса значений случайного процесса по временной оси относительно математического ожидания процесса:

_x(t) = . (9.1.5)

Рис. 9.1.4.

Учитывая последнее выражение, дисперсия случайной величины обычно обозначается индексом ².

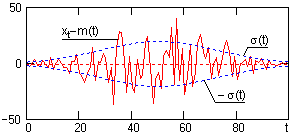
На рис. 9.1.4 приведен пример флюктуационной составляющей процесса X(t) (рис. 9.1.1) в одной из реализаций в сопоставлении со средним квадратическим отклонением ± случайных величин от математического ожидания m(t).

Одномерные законы плотности распределения вероятностей случайных процессов не несут каких-либо характеристик связи между значениями случайных величин для различных значений аргументов.

6. Метод линейного программирования (методика применения на примере траспортной задачи

Модель - условный образ какого-либо объекта, приближенно воссоздающий этот объект с помощью некоторых средств.

Экономико-математическая модель – математическое описание исследуемого экономического процесса или объекта.

Транспортная задача

Постановка состоит в определении оптимального плана перевозок некоторго груза из M пунктов отправления в A₁…A_m в n пунктов назначения B₁…B_n. При этом, в качестве критерия оптимальности берется либо min стоимость перевозок всего груза, либо min время доставки.

Пусть C_i – тарифы перевозки единицы груза из i-го пункута отправления в j-й пункт назначения. A_i – запасы груза в i пункте отправления, B_j – потребности в грузе в j пункте назначения, X_ij – количество единиц груза, перевозимого из i в j пункт.

F – стоимость всех перевозок:

Система ограничений:

Т.о. обеспечивается доставка необходимого количества груза в каждый пункт назначения; вывоз имеющегося груза из всех n отправления и исключаются обратные перевозки.

Неотрицательное решение (X_ij) называется планом транспортной задачи. X*=(X_ij*), при котором F(*)→min, называется оптимальным планом.

Е сли общая потребность в грузе в пункте назначения равна запасу груза в пункте отправления, то ТЗ называются закрытой. (иначе открытой)

Теорема.

Для разрешимости ТЗ необходимо и достаточно, чтобы запасы были равны потребностям.

Если запасы > потребностей, то вводится фиктивный (n+1) пункт назначения. Если наоборот, то вводится фиктивный пункт отправления (m+1).

П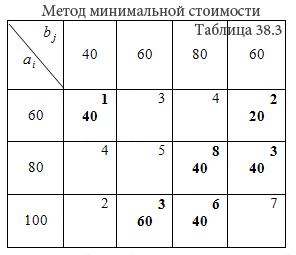 ример:

Среди элементов матрицы стоимостей выбираем наименьшую стоимость C₁₁=1. Данная стоимость имеет место при перевозке груза от 1-го поставщика 1-му потребителю. В соответствующую клетку записываем максимально возможный объем перевозки:

x₁₁ = min {a₁; b₁} = min {60; 40} = 40 т.е. минимум между запасами 1-го поставщика и запросами 1-го потребителя.

2.1. Запасы 1-го поставщика уменьшаем на 40.

2.2. Исключаем из рассмотрения 1-го потребителя, так как его запросы полностью удовлетворены.

3. В оставшейся части матрицы C минимальной стоимостью является стоимость C₁₄=2. Максимально возможная перевозка, которую можно осуществить от 1-го поставщика 4-му потребителю равна x₁₄ = min {a₁'; b₄} = min {20; 60} = 20, где a₁ со штрихом - это оставшиеся запасы первого поставщика.

3.1. Запасы 1-го поставщика исчерпаны, поэтому исключаем его из рассмотрения.

3.2. Запросы 4-го потребителя уменьшаем на 20.

4. В оставшейся части матрицы С минимальная стоимость C₂₄=C₃₂=3. Заполняем одну из двух клеток таблицы (2,4) или (3,2). Пусть в клетку запишем x₂₄ = min {a₂; b₄} = min {80; 40} = 40 .

4.1. Запросы 4-го потребителя удовлетворены. Исключаем его из рассмотрения, вычеркивая 4-й столбец в матрице C.

4.2. Уменьшаем запасы 2-го поставщика 80-40=40.

5. В оставшейся части матрицы C минимальная стоимость C₃₂=3. Запишем в клетку (3,2) таблицы перевозку x₃₂ = min {a₃; b₂} = min {100; 60} =60.

5.1. Исключим из рассмотрения 2-го потребителя. Из матрицы C исключаем 2-ой столбец.

5.2. Уменьшим запасы 3-го поставщика 100-60=40.

6. В оставшейся части матрицы C минимальная стоимость C₃₃=6. Запишем в клетку (3,3) таблицы перевозку x₃₃ = min {a₃'; b₃} = min {40; 80} = 40.

6.1. Исключим из рассмотрения 3-го поставщика, а из матрицы C 3-ю строку.

6.2. Определяем оставшиеся запросы 3-го потребителя 80-40=40.

7. В матрице C остался единственный элемент C₂₃=8. Записываем в клетку таблицы (2,3) перевозку X₂₃=40.

8. Проверяем правильность построения опорного решения.

α проставляются слева вертикально, а β сверху горизонтально. α₁ берется за 0 и дальше, находятся все α и β по формуле: Они должны удовлетворять условиям, что (эти числа называются потенциалами соответствующих пунктов отправления и назначения)

Далее определяют остальные значения неизвестных: для свободных клеток. Если среди них нет положительных, то найденный опорный план оптимальный.

Если существуют , тогда среди них выбирают max и клетку, которой соответствует это число отмечают. Заполняя выбранную клетку нужно изменить объемы поставок, записанные в ряде других занятых клеток или связанных циклом.

Цикл – ломанная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно 2 звена – одно в строке, одно в столбце. Если ломанная, образующая цикл пересекается, то точки пересечения не являются вершинами.

При правильном построении опорного плана, для любой свободной клетки можно построить лишь один цикл. Далее переходим к новому опорному плану, перемещая грузы: 1 пункт – свободной клетке приписывается знак +, остальным поочередно – и +. В свободную клетку переносят меньшее из чисел X_ij, стоящее в – клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в + клетках и вычитают из чисел, стоящих в – клетках. (сдвиг по циклу перерасчета) Число занятых клеток остается неизменным.

7. Принцип максимума. Методика применения на предложенном примере (не давали)

8. Принцип Парето. Границы его применимости. Построение диаграммы Парето по предложенному массиву данных.

П ринцип Парето, или принцип 20/80 — эмпирическое правило, в наиболее общем виде формулируется как «20 % усилий дают 80 % результата, а остальные 80 % усилий — лишь 20 % результата». Может использоваться как базовая установка в анализе факторов эффективности какой-либо деятельности и оптимизации её результатов: правильно выбрав минимум самых важных действий, можно быстро получить значительную часть от планируемого полного результата, при этом дальнейшие улучшения неэффективны и могут быть неоправданны.

Приводимые в законе цифры нельзя считать безусловно точными: это скорее просто мнемоническое правило, нежели реальные ориентиры. Выбор чисел 20 и 80 является также данью заслугам Парето, выявившему конкретную структуру распределения доходов среди итальянских домохозяйств, которой и было свойственно сосредоточение 80 % доходов у 20 % семей. Но любое другое конкретное распределение может иметь другую структуру и для каждой отдельной задачи следует проводить соответствующий анализ, направленный на выявление конкретной зависимости между удельным весом затраченных ресурсов и полученных результатов.

Основная сфера использования закона — экономика, менеджмент, хотя он также эффективен и в политологии

ABC-анализ — метод, позволяющий классифицировать ресурсы фирмы по степени их важности. Этот анализ является одним из методов рационализации и может применяться в сфере деятельности любого предприятия. В его основе лежит принцип Парето — 20 % всех товаров дают 80 % оборота. По отношению к ABC-анализу правило Парето может прозвучать так: надёжный контроль 20 % позиций позволяет на 80 % контролировать систему, будь то запасы сырья и комплектующих, либо продуктовый ряд предприятия и т. п. ЧастоABC-анализ путают с ABC-методом, расшифровывая ABC как Activity Based Costing, что в корне не верно.

ABC-анализ — анализ товарных запасов путём деления на три категории:

• А — наиболее ценные, 20 % — тов.запасов; 80 % — продаж

• В — промежуточные, 30 % — тов.запасов; 15 % — продаж

• С — наименее ценные, 50 % — тов.запасов; 5 % — продаж

В зависимости от целей анализа может быть выделено произвольное количество групп. Чаще всего выделяют 3, реже 4-5 групп.

По сути, ABC-анализ — это ранжирование ассортимента по разным параметрам. Ранжировать таким образом можно и поставщиков, и складские запасы, и покупателей, и длительные периоды продаж — всё, что имеет достаточное количество статистических данных. Результатом АВС анализа является группировка объектов по степени влияния на общий результат.

АВС-анализ основывается на принципе дисбаланса, при проведении которого строится график зависимости совокупного эффекта от количества элементов. Такой график называется кривой Парето, кривой Лоренца или ABC-кривой. По результатам анализа ассортиментные позиции ранжируются и группируются в зависимости от размера их вклада в совокупный эффект. В логистике ABC-анализ обычно применяют с целью отслеживания объёмов отгрузки определённых артикулов и частоты обращений к той или иной позиции ассортимента, а также для ранжирования клиентов по количеству или объёму сделанных ими заказов.

9. Комбинаторные и статистические методы принятия решений. Методика применения на предложенном примере

10. Оптимальность в конфликтных ситуациях.

11. Эволюция научной картины мира. Современная естественнонаучная картина мира. Пространственно-временные масштабы материального мира: микро- макро-, мегомир

Научная картина мира — система представлений человека о свойствах и закономерностях действительности (реально существующего мира), построенная в результате обобщения и синтеза научных понятий и принципов. Использует научный язык для обозначения объектов и явлений материи.

В истории человечества было создано и существовало довольно большое количество самых разнообразных картин мира, каждая из которых отличалась своим видением мира и специфическим его объяснением. Однако прогресс представлений об окружающем мире достигается преимущественно благодаря научному поиску.[2] 

Авторы выделяют либо три, либо четыре научной картины мира. Это связано с признанием времени зарождения науки (либо эпоха античности либо эпоха Нового времени):

Античная или преднаучная.

·     лидер – метафизика (философское учение о сущности мира) с ее умозрительным конструированием модели бытия, с сомнениями относительно адекватности философского видения мира самому реальному миру;

·    следы мифологического культурного наследия, например, то, что боги устанавливают законы этого мира, поэтому знание может быть фрагментарно и по времени и в пространстве;

·  результаты исследований античной натурфилософии - создание атомистики – теории о дискретном строении материи и энциклопедическое описание Аристотелем живой и неживой природы;

·  геоцентрическую астрономическую систему, составленную Клавдием Птолемеем на основании культурного наследия древних;

· есть наличие первоначала мира, субстанция; развитие этих идей привило к образованию атомизма.

·  основными методами познания являются созерцание и озарение или припоминание;

Эти представления сменила механистическая классическая картина мира (XVII -XVIII века).

Естественнонаучные достижения, особенно в механике, породили уверенность в том, что любые процессы в мире могут быть управляемы или рассчитаны так же просто, как рассчитываются или  предсказываются траектории движения небесных тел. В такой Вселенной возможно не только предсказать будущее, но и восстановить прошлое. Считалось: если Бог создал мир в своей основе рациональным, то тогда человек, созданный по образу и подобию божьему, способен познать этот мир.

Европейская наука стартовала с принятия классической научной карты мира, которая была основано на достижениях Галилея и Ньютона.

Классическая картина мира осуществляла описание объектов, как если бы они существовали сами по себе в строго заданной системе координат.

Механистическая картина мира XVII—XVIII веков основывалась на следующих концепциях:

·    Лидер – механика и физика

· Бог – создатель Вселенной, следовательно, в мире все определено и предопределено Создателем; деизм – это представление мира как гигантского часового механизма сотворенного мира, при этом бог удаляется после создания в другой мир;

·   рационализм – это попытка объяснения окружающего мира путем размышления без привлечения сверхъестественных сил; проблема бога уходит из науки;

·   идеалы и нормативы исследования формируются на основе механики и механического понимания природы.

·   методологической основой познания является редукционизм (стремление свести сложное к простому), а основным методом познания 1) индукция – от частного к общему, 2) эмпиризм – признание ведущими методами познания эксперимента, главное в познании – факты, а не причины их появления;

·    теория и практика неразделимы, эксперимент реальный и мысленный – основа познания;

·   измерения и любая количественная оценка имеют определяющий смысл в познании;

·   гуманитарное знание выделяется из общего знания, естественнонаучное знание рассматривается отдельно.

Система понятий в механистической картине мира была неподвижной, негибкой и любое открытие в естествознании, например, появление термо- и электродинамики в физике, Ч.Дарвина в биологии, разрушало ее, так как не находило своего места в ней.

Постепенно усиливался интерес к античной философии, к вопросам понимания в научном познании. В основу познания была положена объективная универсальность Вселенной.

В начале XX века химия, благодаря своим успехам, дополнила физику в базовых построениях картины мира. Молекулярные исследования в биологии и медицине приблизили естествознание к познанию человека как части природы. Оказалось, что выделение гуманитарного знания из общего знания и рассмотрение отдельно взятого естественнонаучного знания противоречит логике устройства единого мира. Сформировалась релятивистская картина мира (неклассическая).

Неклассическая картина мира, пришедшая на смену классической, родилась под влиянием первых теорий термодинамики, оспаривающих универсальность жидкости и газы нельзя представить как чисто механические системы. Переход к неклассическому мышлению был осуществлен в период революции в естествознании на рубеже XIX—XX вв., в том числе и под влиянием теории относительности.

Характеристика

·лидер термодинамика, квантовая механика и теория относительности, отчасти биология

·наука становится определяющей силой общественного прогресса; критика всех иных ненаучных форм описания и познания мира.

·преобладающие идеи – эволюционизм; мир рассматривается как процесс эволюции ставших предметов (то есть развитие их за исключением периодов возникновения и уничтожения); происходит введение относительности пространства и времени, их взаимосвязь с массой;

· стиль мышления – диалектический

· широко распространена вера в объективность и практическую силу знания, позитивный общественный идеал.

· центральной становится проблема соотношения разнообразных методов науки, синтеза дисциплинарно разрозненных знаний и классификации наук.