Практическое занятие №4 Оценка адекватности теоретических решений
Цель занятия: закрепить знания по проверке адекватности уравнения регрессии и объекта исследования.
Теоретические положения
Установление адекватности — это определение ошибки аппроксимации опытных данных. Оценка пригодности гипотезы исследования, а также теоретических данных на адекватность, т. е. соответствие теоретической кривой экспериментальным данным, необходима во всех случаях на стадии анализа теоретико-экспериментальных исследований. Методы оценки адекватности основаны на использовании доверительных интервалов, позволяющих с заданной доверительной вероятностью определять искомые значения оцениваемого параметра. Суть такой проверки состоит в сопоставлении полученной или предполагаемой теоретической функции у=f(х) с результатами измерений. В практике оценки адекватности применяют различные статистические критерии согласия. Одним из таких критериев является критерий Фишера. Для этого необходимо рассчитать экспериментальное (опытное) значение критерия Фишера — KфЭ и сравнить его с теоретическим (табличным) — KфТ принимаемым при требуемой доверительной вероятности Pд (обычно Pд = 0,95). Если KфЭ < KфТ — модель адекватна; если KфЭ > KфТ — модель неадекватна.
Методические рекомендации
Результаты расчета представить в виде табл.4.2, сделать вывод об адекватности теоретической зависимости. Расчетное значение критерия Фишера определяется по зависимости:
.
(4.1)
где DA - дисперсия адекватности;
DЭ - средняя дисперсия всего эксперимента.
Дисперсия адекватности:
(4.2)
18
где
-
значение функции, вычисленное по
уравнению регрессии для факторов
i - го опыта (рассчитывается по зависимости, полученной на 3-м
практическом занятии);
-
среднее экспериментальное значение
функции в i - м
опыте (табл. 4.1);
n – число измерений в одной серии опытов ( n = 5 );
d – число коэффициентов уравнения теоретической регрессии;
Средняя дисперсия всего эксперимента:
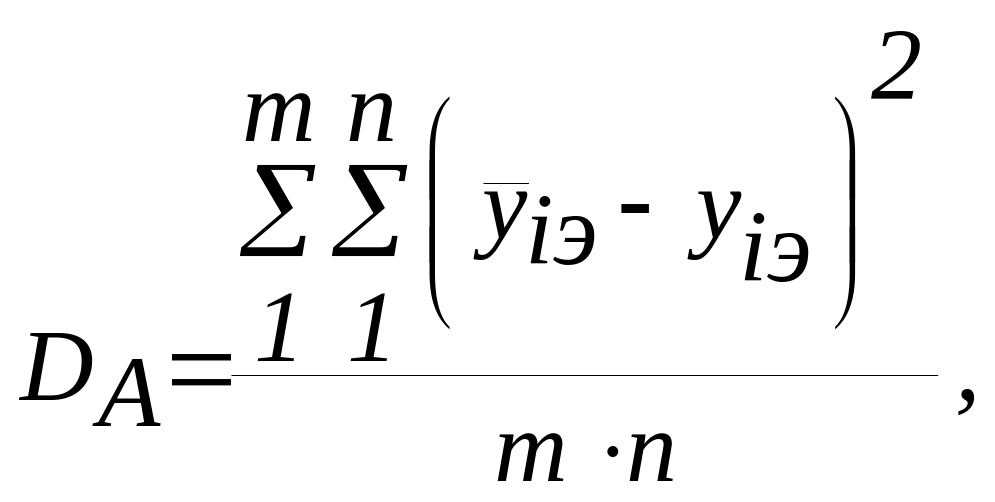
где
-
текущее экспериментальное значение
функции в i
- м опыте;
m – число серий опытов ( m = 3);
Значение КфТ принимается для доверительной вероятности 0,95 и числа степеней свободы q1 = п – d; q2 = п ·( m – 1 ).
Критерий Фишера КфТ
q1 |
q2 |
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
12 |
24 |
|
1 |
16 |
19 |
21 |
22 |
23 |
23 |
24 |
24 |
2 |
18 |
19 |
19 |
19 |
19 |
19 |
19 |
19 |
3 |
10 |
9.6 |
9.3 |
9.1 |
9.0 |
8.9 |
8.7 |
8.6 |
4 |
7.7 |
6.9 |
6.6 |
6.4 |
6.3 |
6.2 |
5.9 |
5.8 |
Таблица 4.1
Исходные данные
№ вар |
№ опыта |
Х1 |
Х2 |
Y1э |
Y2э |
Y3э |
1 |
1 |
10 |
3 |
154.21 |
144.92 |
151.01 |
2 |
14.5 |
6 |
305.69 |
297.69 |
308.25 |
|
3 |
19 |
5 |
358.22 |
351.48 |
354.76 |
|
4 |
23.5 |
6 |
489.95 |
480.48 |
491.42 |
|
5 |
28 |
7 |
639.47 |
623.34 |
638.00 |
19
Продолжение табл. 4.1
№ вар |
№ опыта |
Х1 |
Х2 |
Y1э |
Y2э |
Y3э |
2 |
1 |
19 |
10 |
512.60 |
495.21 |
505.27 |
2 |
22 |
20.5 |
1146.47 |
1147.26 |
1139.67 |
|
3 |
25 |
17 |
1041.80 |
1042.26 |
1041.92 |
|
4 |
28 |
20.5 |
1414.74 |
1403.83 |
1402.08 |
|
5 |
31 |
24 |
1750.68 |
1755.32 |
1752.10 |
|
3 |
1 |
3 |
4 |
109.63 |
104.08 |
107.84 |
2 |
4.5 |
10 |
377.24 |
374.95 |
371.85 |
|
3 |
6 |
8 |
399.16 |
395.22 |
401.49 |
|
4 |
7.5 |
10 |
619.45 |
613.17 |
614.80 |
|
5 |
9 |
12 |
882.74 |
879.22 |
878.14 |
|
4 |
1 |
5 |
4 |
176.76 |
176.44 |
171.91 |
2 |
7 |
13 |
717.82 |
709.16 |
704.90 |
|
3 |
9 |
10 |
693.80 |
693.85 |
695.13 |
|
4 |
11 |
13 |
1104.60 |
1093.07 |
1096.61 |
|
5 |
13 |
16 |
1547.05 |
1548.95 |
1547.73 |
|
5 |
1 |
-1 |
-2 |
3.47 |
5.70 |
7.61 |
2 |
2 |
4 |
34.51 |
33.04 |
28.88 |
|
3 |
5 |
2 |
36.67 |
38.70 |
36.50 |
|
4 |
8 |
4 |
83.63 |
92.69 |
87.68 |
|
5 |
11 |
6 |
167.84 |
167.24 |
170.96 |
|
6 |
1 |
5 |
5 |
7.95 |
11.98 |
5.01 |
2 |
10 |
27.5 |
22.13 |
19.94 |
18.73 |
|
3 |
15 |
20 |
14.48 |
17.78 |
21.52 |
|
4 |
20 |
27.5 |
23.05 |
20.48 |
17.26 |
|
5 |
25 |
35 |
23.53 |
23.95 |
24.00 |
|
7 |
1 |
25 |
20 |
48.28 |
43.90 |
45.29 |
2 |
32.5 |
32 |
86.28 |
82.19 |
85.41 |
|
3 |
40 |
28 |
96.78 |
91.28 |
89.59 |
|
4 |
47.5 |
32 |
117.83 |
120.43 |
119.41 |
|
5 |
55 |
36 |
159.78 |
152.16 |
156.34 |
20
Продолжение табл. 4.1
8 |
1 |
0 |
2 |
12.29 |
16.84 |
8.50 |
2 |
2 |
17 |
202.02 |
205.47 |
204.59 |
|
3 |
4 |
12 |
238.62 |
242.01 |
245.54 |
|
4 |
6 |
17 |
487.62 |
489.32 |
481.50 |
|
5 |
8 |
22 |
788.69 |
793.56 |
788.38 |
|
9 |
1 |
3 |
2 |
70.75 |
63.06 |
63.14 |
2 |
5 |
9.5 |
366.03 |
363.04 |
355.45 |
|
3 |
7 |
7 |
401.60 |
394.14 |
397.87 |
|
4 |
9 |
9.5 |
688.53 |
686.99 |
687.68 |
|
5 |
11 |
12 |
1015.71 |
1006.34 |
1008.00 |
|
10 |
1 |
4 |
1 |
78.40 |
84.45 |
81.77 |
2 |
8 |
14.5 |
304.89 |
304.83 |
308.76 |
|
3 |
12 |
10 |
340.07 |
335.51 |
334.06 |
|
4 |
16 |
14.5 |
556.68 |
559.87 |
549.46 |
|
5 |
20 |
19 |
907.48 |
903.34 |
908.19 |
|
11 |
1 |
5 |
5 |
159.24 |
161.85 |
163.94 |
2 |
12.5 |
20 |
1323.99 |
1315.28 |
1315.04 |
|
3 |
20 |
15 |
1553.95 |
1549.26 |
1551.83 |
|
4 |
27.5 |
20 |
2879.34 |
2859.41 |
2866.71 |
|
5 |
35 |
25 |
4440.98 |
4442.31 |
4441.31 |
|
12 |
1 |
10 |
6 |
445.55 |
436.04 |
439.69 |
2 |
13 |
16.5 |
1395.37 |
1401.80 |
1397.89 |
|
3 |
16 |
13 |
1382.81 |
1373.99 |
1381.42 |
|
4 |
19 |
16.5 |
2031.71 |
2035.18 |
2037.98 |
|
5 |
22 |
20 |
2814.83 |
2820.43 |
2821.00 |
|
13 |
1 |
25 |
16 |
1344.58 |
1346.20 |
1345.75 |
2 |
30 |
22 |
2172.72 |
2169.09 |
2175.14 |
|
3 |
35 |
20 |
2282.29 |
2284.10 |
2281.84 |
|
4 |
40 |
22 |
2848.91 |
2841.34 |
2842.73 |
|
5 |
45 |
24 |
3463.51 |
3465.60 |
3466.71 |
|
14 |
1 |
20 |
13 |
21.21 |
23.02 |
18.28 |
2 |
30 |
34 |
66.13 |
67.92 |
64.33 |
|
3 |
40 |
27 |
67.43 |
72.04 |
69.43 |
|
4 |
50 |
34 |
98.95 |
97.22 |
100.08 |
|
5 |
60 |
41 |
139.17 |
139.70 |
139.06 |
21
Продолжение табл. 4.1
№ вар |
№ опыта |
Х1 |
Х2 |
Y1э |
Y2э |
Y3э |
15 |
1 |
1 |
5 |
68.33 |
69.10 |
72.48 |
2 |
1.5 |
9.5 |
132.50 |
132.72 |
129.10 |
|
3 |
2 |
8 |
136.36 |
134.73 |
139.05 |
|
4 |
2.5 |
9.5 |
182.52 |
188.68 |
187.94 |
|
5 |
3 |
11 |
231.38 |
225.26 |
229.75 |
|
16 |
1 |
2 |
2 |
64.02 |
66.30 |
69.37 |
2 |
3.5 |
9.5 |
214.59 |
201.81 |
205.82 |
|
3 |
5 |
7 |
227.69 |
228.22 |
229.60 |
|
4 |
6.5 |
9.5 |
351.81 |
350.50 |
345.60 |
|
5 |
8 |
12 |
536.81 |
529.47 |
535.71 |
|
17 |
1 |
4 |
19 |
748.15 |
751.97 |
751.05 |
2 |
9 |
26.5 |
2029.63 |
2041.78 |
2035.14 |
|
3 |
14 |
24 |
2870.87 |
2875.45 |
2874.98 |
|
4 |
19 |
26.5 |
4067.20 |
4059.71 |
4024.19 |
|
5 |
24 |
29 |
5812.68 |
5812.32 |
5819.52 |
|
18 |
1 |
6 |
0.1 |
22.55 |
26.91 |
25.90 |
2 |
13 |
0.85 |
54.48 |
50.62 |
49.79 |
|
3 |
20 |
0.6 |
74.29 |
74.23 |
74.76 |
|
4 |
27 |
0.85 |
97.13 |
92.26 |
98.56 |
|
5 |
34 |
1.1 |
124.17 |
116.73 |
116.50 |
|
19 |
1 |
4 |
0.7 |
23.14 |
24.49 |
22.14 |
2 |
5 |
1.45 |
43.42 |
46.39 |
45.02 |
|
3 |
6 |
1.2 |
47.30 |
46.81 |
51.47 |
|
4 |
7 |
1.45 |
56.87 |
63.46 |
59.85 |
|
5 |
8 |
1.7 |
72.98 |
77.82 |
81.16 |
|
20 |
1 |
5 |
-1 |
10.02 |
14.06 |
17.87 |
2 |
6.5 |
6.5 |
244.69 |
249.82 |
250.57 |
|
3 |
8 |
4 |
192.05 |
187.54 |
191.73 |
|
4 |
9.5 |
6.5 |
243.44 |
260.61 |
258.94 |
|
5 |
11 |
9 |
494.95 |
487.98 |
493.77 |
22
Продолжение табл. 4.1
№ вар |
№ опыта |
Х1 |
Х2 |
Y1э |
Y2э |
Y3э |
21 |
1 |
25 |
33 |
52.44 |
57.66 |
53.54 |
2 |
37.5 |
55.5 |
78.61 |
80.04 |
77.40 |
|
3 |
50 |
48 |
123.44 |
128.03 |
129.19 |
|
4 |
62.5 |
55.5 |
207.12 |
198.64 |
199.86 |
|
5 |
75 |
63 |
219.59 |
221.93 |
216.18 |
|
22 |
1 |
15 |
8 |
221.19 |
226.11 |
223.31 |
2 |
19 |
21.5 |
667.87 |
670.00 |
670.28 |
|
3 |
23 |
17 |
657.78 |
647.88 |
652.44 |
|
4 |
27 |
21.5 |
917.66 |
909.19 |
906.70 |
|
5 |
31 |
26 |
1319.37 |
1314.07 |
1314.00 |
|
23 |
1 |
9 |
7 |
482.96 |
487.77 |
487.54 |
2 |
11.5 |
20.5 |
1654.23 |
1651.44 |
1650.04 |
|
3 |
14 |
16 |
1554.84 |
1555.67 |
1556.77 |
|
4 |
16.5 |
20.5 |
2292.70 |
2289.90 |
2287.78 |
|
5 |
19 |
25 |
3160.17 |
3164.77 |
3163.24 |
|
24 |
1 |
26 |
7 |
65.40 |
67.72 |
69.53 |
2 |
29 |
17.5 |
105.97 |
105.08 |
102.41 |
|
3 |
32 |
14 |
96.32 |
97.44 |
97.41 |
|
4 |
35 |
17.5 |
118.37 |
119.26 |
119.13 |
|
5 |
38 |
21 |
139.62 |
142.78 |
141.63 |
|
25 |
1 |
17 |
11 |
165.41 |
172.11 |
168.34 |
2 |
18.5 |
17 |
292.71 |
281.19 |
282.82 |
|
3 |
20 |
15 |
231.99 |
229.33 |
227.05 |
|
4 |
21.5 |
17 |
263.44 |
267.54 |
268.19 |
|
5 |
23 |
19 |
7.54 |
0.90 |
6.89 |
23
Таблица 4.2
Результаты эксперимента и оценка адекватности его теоретического представления
№ вар |
№ опыта |
Х1 |
Х2 |
Y1э |
Y2э |
Y3э |
Yiэ |
Yiт |
Di |
Di m |
Dа |
Критерий Фишера расчетный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|