Запитання для самоперевірки

1. Визначити основні завдання курсу опору матеріалів.

2. Що розуміють під міцністю, жорсткістю і стійкістю матеріалів?

3. Як в опорі матеріалів класифікуються зовнішні сили?

4. Дати визначення внутрішніх сил. Чим відрізняється поняття внутрішніх сил у курсі опору матеріалів від означення цих сил у фі­зиці? Які ви знаєте внутрішні силові фактори?

5. Розкажіть про призначення і сутність методу перерізів.

6. Що таке епюра внутрішніх силових факторів? Розкажіть правила побудови епюр.

7. Які гіпотези використовують у курсі опору матеріалів?

8. Що таке деформація тіла? Які види деформацій вам відомі?

9. Що таке напруга в точці перерізу тіла? Її одиниці.

ВИКЛАДАЧ____________________

РОЗДІЛ:Опір матеріалів

ТЕМА Розтяг і стиск

ПЛАН

1. Аналіз напруженого стану при одновісьовому розтязі

2. Максимальні дотичні напруження

Студент повинен знати: визначення деформації розтягу (стиску), методи визначення нормальних та дотичних напружень при розтязі (стиску).

Студент повинен вміти:визначати максимальні нормальні і дотичні напруження в довільних перерізах брусу..

ЛІТЕРАТУРА ОСНОВНА [ 2 ] §§2.3-2.4; 1 зад. № 134 (б) ; [12] §§ 3,2

ЛІТЕРАТУРА ДОДАТКОВА

Конспект лекції Лінійний напружений стан

Лінійний напружений стан має місце в точках стержня , який розтягують або стискують поздовжньою силою. Розглянемо стержень призматичної фор­ми з площею поперечного перерізу А, навантажений - зосередженими роз­тягуючими силами F /рас.3.5/. На достатній відстані від місця при­кладання сили /відповідно до принципу Сен-Венана /виберемо точку В і проведемо через цю точку поперечний переріз. Нормальна напруга в будь-якій точці цього перерізу,в тому числі і в точці В, визначається за отриманою раніше формулою

/3.3/

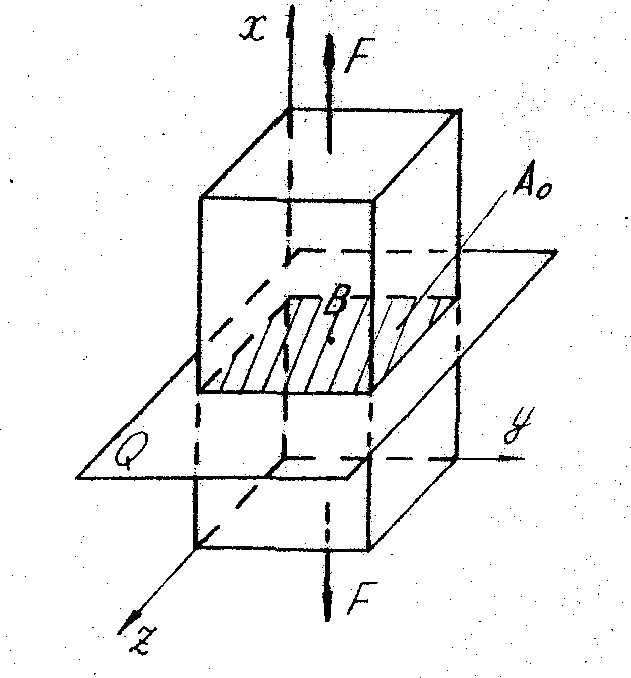
Рис. 3.5. До визначення напруги в точці В при лінійному напруженому стані.

Рис. 3.6. Зображення лінійного напруженого стану : а – в просторі, б – на площині.

Оскільки при розтягу стерж­ня його напружений стан одно­рідний, то для дослідження на­пруг на різних похилих площад­ках уявно вирізаний паралеле­піпед може бути довільних роз­мірів, в тому числі і такий, що мав за грань поперечний переріз стержня А₀. На верхній і ниж­ній гранях паралелепіпеда па­ралельних площині А₀ , діють розтягуючі напруги, які визна­чаються формулою /3.3/. На всіх бічних гранях нормальні напру­ги відсутні, тому що відсутні діючі сили. Дотичні напруги на всіх гранях дорівнюють нулю, оскільки розтягуючі сили F не утворюють зсуву виділених граней паралелепіпеда.

Оскільки на гранях паралелепіпеда відсутні дотичні напруги, то нормальні напруги тут будуть головними, і відповідно до формули /3.2/ дістанемо у₁ = у = F/A₀, у₂ = 0, у₃ = 0 тобто кожна точка виділеного паралелепіпеда перебуває в лінійному напруженому ста­ні /рис.3.6.б/. Надалі елемент, що перебуває в лінійному або плоскому напруженому стані, будемо зображати перерізом паралелепіпеда у вигляді плоскої фігури /рис.3.6,б/.

У такий спосіб зображення лінійного і плоского напруже­них станів можна ввести більш просте правило знаків для до­тичних напруг, не пов’язане з вибором системи координат: дотичні напруги на площині додатні, якщо вони намагають­ся повернути розглядуваний елемент відносно довільної точки, взятої всередині елемента за ходом годинникової стрілки, і від’ємні і від'ємні – якщо проти годинникової стрілки.

Розглянемо як розподілені напруги на площині похилого перерізу. Для цього проведемо площину, нормаль n_б до якої віссю х паралелепіпеда утворює кут б /рис.3.7/ На похилій плоєні Аб повну напругу Рб , зумовлену силами F , можна визначати за формулою

Оскільки площи­на Аб зв'язана з А₀ співвідношенням Аб = A /cos б , то

де враховано, що F / A₀ = у_1. Проекція повної напруги Рб на нормаль n_б утворює нормальну напругу , або на підставі /3.5/

/3.6/

Користуючись рівнянням /3.6/, можна простежити за зміною зна­чень нормальної напруги на площадках, що мають різний нахил. Так, із збільшенням кута б від 0 до 90° напруга у зменшується від значення у₁ = у₂ при б = 0 до нуля при б = 90°.

Отже, най­більше значення нормальної напруги маємо на головній площадці, де

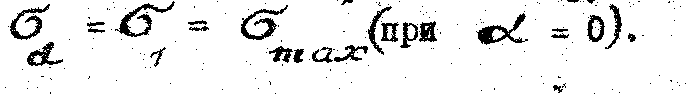
Проекція напруг Рб на площадку Аб утворює на ній дотичну напругу Аб, яку можна визначити за формулою Аб = Рб ^sinб або згідно з /3.5/.

/3.7/

Відповідно до формули /3.7/ найбільші дотичні напруги виникають на площадці з sin 2б = 1, тобто для якої 2б = 90° і б = 45°. Значить, на площадці, нормаль до якої з напрямом поздовжньої осі х утворює кут 45°, дотичні напруги досягають найбільших значень

/3.8/

При стиску головні напруги мають значення у₁ = у₂ = 0; у₃ = -F /A₀. Тоді напружений стан у точці стержня визначається, як і при розтягу, формулами /3.6/ і /3.7/, лише в них замість у₁ не­обхідно підставляти у₃.

Приклад 3.1. Визначити нормальні і дотичні напруги в точці В перерізу 1-1 і в точці С перерізу 2-2 стержня, якщо його площа поперечного перерізу А_о = 20 • 10^-4 м², б₁ = 30⁰, б₂ = 40°. Стер­жень навантажений зовнішніми силами F₁ = 40 кН і F₂ = 72 кН так, як показано на рис.3.8,а.

Розв'язання. Перш за все розбиваємо стержень на ділянки і, вико­ристовуючи метод перерізів, визначимо значення поздовжніх сил N₁, N₂ на кожній із них: N_{1 =} F₁ - F₂ = 40 – 72 = - 32 кН /стиск/. Побудуємо епюру нормальних сил /рисЗ.8,б/.

Знайдемо нормальну напругу в поперечному перерізі, що проходить через точку В:

Зазначимо, що оскільки на даній ділянці виділений елемент підлягає стиску, то в точці В маємо напругу у_{х =} у₃ .

Аналогічно напруга в поперечному перерізі, що проходить через точ­ку С, буде

Елементи, виділені на ділянках точок В і С, головні напруги у₃ і у₁ , а також похилі площини та невідомі поки напруги на них, показані на рис.3.9, 3.10. Визна­чимо нормальні у_б1 і дотичні А_б1 напруги на похи­лій площині, утвореній перері­зом 1-1.

Рис. 3.8. Епюра нормальної сили N в стержні навантаженому силами F₁ і F₂

Рис.3.9. Схема до визначання напруг у_б і А_б в точці В стержня , зображеного на рис.3.8

Рис. 3.10. Схема до визначення напруг у_б та А_б в точці С стержня, зображеного на рис. 3.8.

Відносно напряму осі х /або у₃ / нормаль n_{б ,} утворює кут б₁ , який відраховується за годинниковою стрілкою. Тому, підставляючи кут б₁ в формули /3.6/ і /3.7/, його необхідно брати із знаком "мінус" Тоді за формулами /3.6/ і /3.7/

Аналогічно, враховуючи знак кута б₂ , визначаємо напруги на похилій площині, яка утворена перерізом 2-2:

ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ

1. Дати визначення лінійного, плоского і об'ємного напружених станів. Навести приклади.

2. Які правила знаків вводяться для нормальних і дотичних напруг?

3. Доведіть, що сума нормальних напруг на двох довільних взаємно перпендикулярних площадках, що проходять через дану точку навантаже­ного тіла, величина стала.

4. Що таке головні площини і головні напруги?

ВИКЛАДАЧ____________________

РОЗДІЛ:Опір матеріалів

ТЕМА Розтяг і стиск

ПЛАН

1. Статично невизначені системи

2. Температурні і монтажні напруження

Студент повинен знати: визначення. статично невизначеним системам, принципи розв’язання задач статично невизначених систем

Студент повинен вміти:визначати реакції опори статично невизначених систем.

ЛІТЕРАТУРА ОСНОВНА [ 2 ] §§ 2.10,2.11; [12] §§ 2.8, 2.9

ЛІТЕРАТУРА ДОДАТКОВА