Лабораторная работа № 6 Элементы корреляционно-регрессионного анализа

Цель: научиться определять коэффициент корреляции для случайной величины (Y, Х), оценивать его значимость и строить функцию линейной регрессии Y на X.

Теория. С помощью корреляционного анализа изучается теснота взаимосвязи между исследуемыми случайными величинами. Для этого вводится статистический коэффициент корреляции

,

где – статистический (несмещенный) корреляционный момент, определяемый при неизвестных математических ожиданиях Х и Y следующими формулами:

– для простого статистического ряда;

– для сгруппированных данных, где ; – представители разрядов; .

Таким образом,

– для простого статистического ряда;

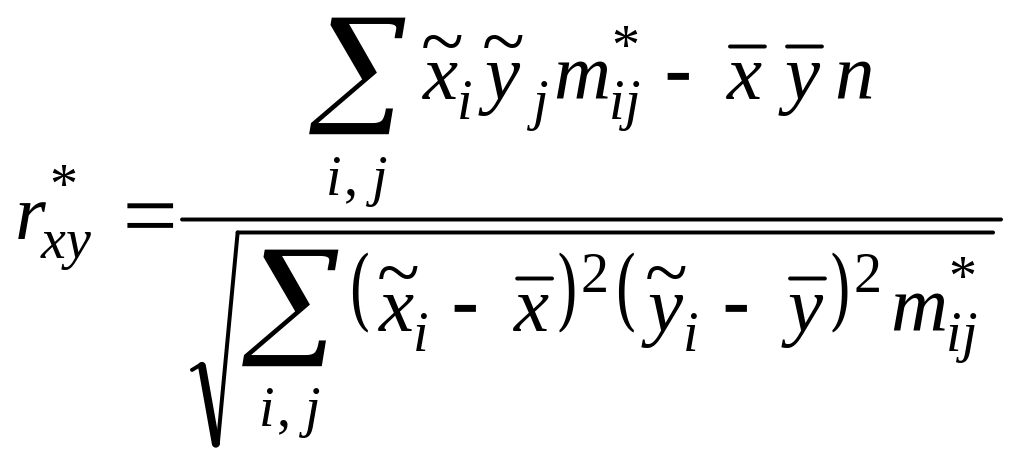– для сгруппированных данных.

Пусть X и Y – нормально распределенные случайные величины и статистический коэффициент корреляции . Гипотеза о независимости случайных величин Х и Y, т.е. гипотеза при проверяется следующим образом:

1. вычисляется величина

,

которая имеет распределение Стьюдента с степенями свободы;

2. по таблице распределения Стьюдента определяется ;

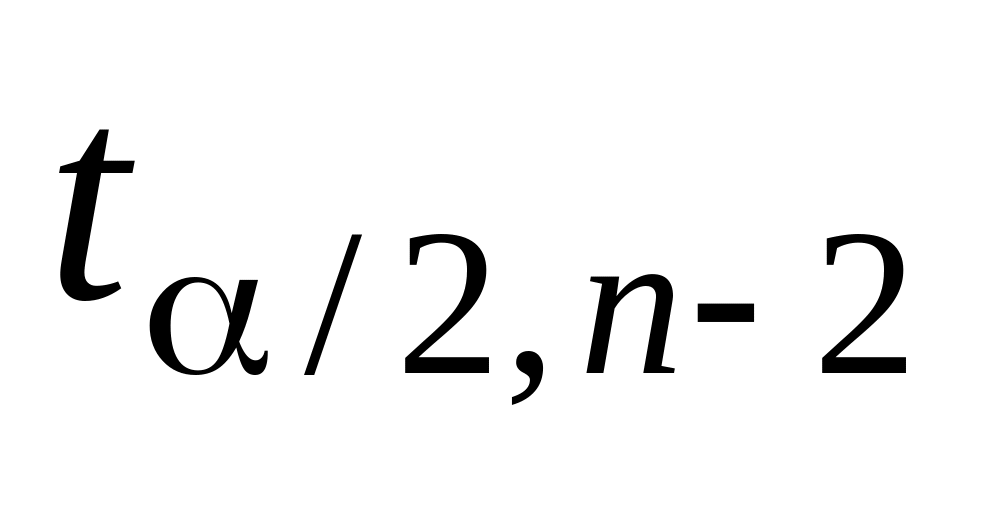3. если  , то значим и случайные величины Х и Y стохастически зависимы (связью Х и Y пренебрегать нельзя);

4. если < , то = 0 и Х и Y – независимые случайные величины.

Уравнение регрессии можно записать в виде

.

Для оценки объяснимой части вариации ко всей вариации в целом вводится коэффициент детерминации , который показывает, на сколько процентов в среднем вариация результативной величины объясняется за счет вариации факторной величины.

Задание №1. Экономическое обследование зависимости выпуска готовой продукции на одного работающего от энерговооруженности труда работающего 5 предприятий дало результаты, приведенные в табл. 7. Провести корреляционно-регресионный анализ при уровне значимости  = 0,01.

Таблица 7

Энерговооруженность труда работающего, кВт ч	3	4	6	7	10
Выпуск готовой продукции на одного работающего, тыс. руб.	3	5	6	7	9

Решение. Пусть Х – энерговооруженность труда работающего, Y – выпуск готовой продукции на одного работающего. Для несгруппированных данных для расчетов удобно пользоваться таблицей, приведенной на рис. 28.

В Microsoft Excel предусмотрена встроенная функция для расчета квантилей распределения Стьюдента =СТЬЮДРАСПОБР (вероятность; степени_свободы), где вероятность – вероятность, соответствующая двустороннему распределению Стьюдента ( / 2); степени_ свободы – число степеней свободы k, характеризующее распределение.

	A	B	C	D	E	F
1	i	x	y	xy	x2	y2
2	1	3	3	= B2 * C2	= B2^2	= C2^2
3	2	4	5
4	3	6	6
5	4	7	7
6	5	10	9
7	Сумма	= СУММ (B2:B6)	= СУММ (C2:C6)	= СУММ (D2:D6)	= СУММ (E2:E6)	= СУММ (F2:F6)
8	=	= B7 / 5	=	= C7 / 5	=	= E7 / 5
9	=	= F7 / 5	=	= D7 / 5	х* =	= КОРЕНЬ (F8 – B8^2)
10	у* =	=КОРЕНЬ (B9 – D8^2)	r* =	=(D9 – B8* D8)/F9/B10
11	t* =	=D10*КОРЕНЬ (3)/ КОРЕНЬ (1 – D10^2)	t(0,005; 3)	= СТЬЮД РАСПОБР (0,01;3)
12	d* =	=D10^2
13	уравнение регрессии	y =	=D8 –D10* B10*B8/F9	+	= D10* B10 / F9	x

Р и с. 28

В результате расчетов получим: = 6; = 6; = 42; = 40; = 40,8; _х* = 2,45; _у* = 2; r* = 0,98; t* = 1,698; t_{0,005; 3} = 5,84.

Поскольку , гипотеза H₀ отвергается   значим и случайные величины Х и Y коррелированы.

Для проверки полученного коэффициента корреляции можно воспользоваться встроенной функцией = КОРРЕЛ (массив1; массив2), где массив1 – это ячейка интервала значений случайной величины Х, массив2 – это второй интервал ячеек со значениями случайной величины Y. Для задания №1 эта функция будет иметь вид = КОРРЕЛ (В2:В6; С2:С6).

Коэффициент детерминации 96%, следовательно, 96% общей вариабельности выпуска готовой продукции на одного работающего объясняется изменением энерговооруженности труда работающего, в то время как на остальные факторы приходится 4% вариабельности.

Статистическое уравнение регрессии имеет вид у = 0,8 х + 1,2.

Из уравнения следует, что если энерговооруженность труда работающего возрастет на одну единицу, то выпуск готовой продукции на одного работающего увеличится в среднем на 0,8 (тыс. руб.).

В составе Microsoft Excel существует встроенная функция для регрессионного анализа ЛИНЕЙН, которая вычисляет угловой коэффициент m и отрезок b (свободный член) на оси ОY, отсекаемый прямой линией y = mx + b.

Функция имеет вид ЛИНЕЙН (известные_значения_y; известные_значения_x; конст; статистика), где известные_значения_y – множество значений y, которые уже известны для соотношения y = mx + b, известные_значения_x – необязательное множество значений x, конст – логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0 (если конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом, если аргумент конст имеет значение ЛОЖЬ, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y = mx); статистика – логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику, если аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b. Функцию ЛИНЕЙН необходимо вводить как функцию массива. Если формула не будет введена как формула массива, единственное значение будет равно m.

Для нашего примера функция будет иметь вид = ЛИНЕЙН (С2:С9; В2:В9; 1; 0). Далее надо выделить две ячейки, где будут размещены m и b, нажать клавишу F2, а затем – клавиши CTRL + SHIFT + ENTER.

Подставляя в уравнение регрессии значение х, найдем соответствующее значение у, т.е. выполним прогноз. Так, если энерговооруженность труда составит 11 единиц, то выпуск готовой продукции на одного работающего в среднем будет 10 тыс. руб.

Построим исходные данные и нанесем график полученного уравнения на рис. 29. Для этого надо:

1. Войти в Мастер диаграмм, на вкладке Стандартные из списка Тип выбрать Точечная, а из списка Вид – Точечная диаграмма позволяет сравнивать пары значений. Затем щелкнуть по кнопке Далее.

2. На втором шаге на вкладке Диапазон данных указать В2:С6, Ряды в … – столбцах, на вкладке Ряд / Имя: исходные данные. Затем щелкнуть по кнопке Далее.

3. На третьем шаге на вкладке Заголовки внести все подписи. На вкладке Линии сетки установить флажки основные линии для осей Х и Y. На вкладке Легенда – установить флажок Добавить легенду / внизу. Затем щелкнуть по кнопке Далее.

4. На четвертом шаге надо разместить диаграмму на том же листе. Затем щелкнуть по кнопке ОК.

5. Для нанесения линии регрессии надо выделить точки на графики, правой кнопкой мыши вызвать контекстное меню и выбрать Нанести линию тренда… На вкладке Тип выбрать Линейная, на вкладке Параметры / Название аппроксимирующей (сглаживающей кривой) / другое: указать – линия регрессии и установить флажок Показывать уравнение на диаграмме.

6. В результате выполненных действий появятся исходные данные и линия регрессии, изображенные на рис. 29.

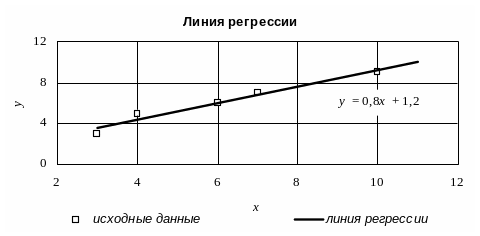
Р и с. 29

7. Для проведения прогнозирования надо:

• щелкнуть мышкой по линии регрессии,

• войти в меню Формат линии тренда / Параметры,

• установить флажок Прогноз вперед на 1 единицу. 

Задание №2. Пусть наблюдается выборка, состоящая из 10 студентов. Х – их оценка по высшей математике за первый курс, Y – оценка, полученная на экзамене по математической статистике (см. табл. 8). Провести корреляционно-регресионный анализ случайных величин Х и Y при  = 0,1.

Таблица 8

i	1	2	3	4	5	6	7	8	9	10
X	3	3	3	4	4	4	4	5	5	5
Y	2	3	3	3	3	3	5	4	4	5

Решение. Составим корреляционную таблицу для сгруппированных данных (см. рис. 30). Здесь , , где суммирование распространяется на все возможные значения индексов j или i. .

	А	B	C	D	E	F	G	H
17		2	3	4	5
18	3	1	2			= СУММ (B18:E18)	=A18*F18	=A18^2*F18
19	4		3		1
20	5			2	1
21		= СУММ (B18:B20)				= СУММ (F18:F20)
22		= B17*B21				= СУММ (B22:E22)
23		= B17^2*B21				= СУММ (B23:E23)
24		= $A$18*B18+ $A$19*B19+ $A$20*B20
25		= B17*B24				= СУММ (B25:E25)

Р и с. 30

Составим таблицу для расчета числовых характеристик и проверки гипотезы при (рис. 31).

В результате расчетов получили: = 4; = 3,5; = 16,6; = 13,1; = 40,8; _х* = 0,77; _у* = 0,85; r* = 0,7; t* = 2,77; t_{0,05; 8} = 1,86.

	A	B	C	D	E	F
26	=	= G21 / 10	=	= F22 / 10
27	=	= H21 / 10	=	= F23 / 10	х* =	= КОРЕНЬ (В27 / 10–В26^2)
28	у*=	= КОРЕНЬ (D27 / 10 –D26^2)	r* =	=(F25 / 10 –B26 *D26)/ F26 / B28
29	t* =	= D28* КОРЕНЬ (8) / КОРЕНЬ (1 – D28^2)	t(0,05; 8) =	= СТЬЮД РАСПОБР (0,1; 8)
30	d* =	=D28^2
31	уравнение регрессии	y =	= D26 –D28*B28*B26 /F27	+	=D28*B28 / F27	x

Р и с. 31

Поскольку , гипотеза H₀ отвергается   значим и случайные величины Х и Y коррелированны, т.е. оценки на экзамене по математической статистике существенно зависят от оценок по высшей математике.

Коэффициент детерминации 49%, следовательно, 49% общей вариабельности оценок на экзамене по математической статистике объясняется изменением оценки по высшей математике, в то время как на остальные факторы приходится 51% вариабельности.

Статистическое уравнение регрессии имеет вид .

Нанесем исходные данные (точки (x_i, у_j), ) и линию регрессии на график (рис. 32).

Подсчитаем условные средние по формуле

.

Для этого в ячейку В32 введем заголовок условные средние Y, в ячейки А33:А35 введем значения случайной величины Х (3, 4, 5), а в ячейку В33 введем формулу =($B$17*B18 + $C$17*C18 + $D$17*D18 + $E$17*E18) / F18 и скопируем ее в диапазон В34:В35.

Для нанесения эмпирической линии регрессии (x_i, ) на график надо:

• выделить диапазон А32:В35, зацепить его мышкой и перетащить на диаграмму;

• в появившемся меню Специальная вставка установить флажки новые ряды в столбцах и отметить Имена рядов в первой строке, Категории (значения оси Х) в первом столбце;

• в результате выполненных действий на диаграмме (рис. 32) появятся маркеры нового ряда. 

Р и с. 32

Задание №2. На основании индивидуальных исходных данных варианта РГР для случайных величин Х и Y провести корреляционно-регресионный анализ при уровнях значимости  = 0,01 и  = 0,05 (более подробно см. лабораторную работу № 8, п. 6).