Лабораторная работа № 5 Проверка гипотезы о виде закона распределения

Цель: по виду гистограммы и статистической функции распределения научиться выдвигать и проверять нулевую гипотезу о виде закона распределения случайной величины.

Теория. Пусть эмпирическое распределение задано в виде последовательности интервалов одинаковой длины и соответствующих им частот.

Для расчета теоретических частот по нормальному, экспоненциальному и равномерному законам воспользуемся формулой

,

где Р_i – соответствующая вероятность попадания Х в интервалы (х_i; x_i+1), n – объем выборки.

Для нормального закона распределения , , – среднее; * – статистическое среднее квадратическое отклонение;

для экспоненциального – , где  = 1 / ;

для равномерного на промежутке (а, b) – , где оценки параметров а и b находятся по формулам а* = – , b* = + .

Проверка гипотезы о виде закона распределения осуществляется с использованием критерия Пирсона. При этом количество степеней свободы k

• для нормального и равномерного законов k = r – 3;

• для показательного закона k = r – 2.

Задание №1. В локомотивном депо были проанализированы данные о суточном расходе материала А. Анализом был охвачен расход материала за каждый из 200 наугад отобранных рабочих дней (см. табл. 6). Необходимо выдвинуть и проверить гипотезу при уровне значимости  = 0,05 о виде закона распределения. Рассмотреть нормальный, экспоненциальный и равномерный законы.

Таблица 6

Интервалы удоев на одну корову, тыс. л	190–200	200–210	210–220	220–230	230–240	240–250
Количество коров	7	14	38	62	54	25

Решение. Пусть случайная величина Х – суточный расход материала А. Для расчетов и построения графиков составим таблицу, приведенную на рис. 25.

В ячейках А2:С7 введены исходные данные, в ячейках В9, D9 и F9 – числовые характеристики выборки. В диапазоне D2:D7 приведены статистическая плотность распределения, в ячейках G2:I7 – теоретические плотности распределения, рассчитанные с использованием встроенных функций.

Если выдвинута гипотеза о нормальном законе распределения, то удобно пользоваться встроенной функцией = НОРМРАСП (x; среднее; стандартное_откл; интегральная), где x – значение, для которого строится распределение, среднее – среднее арифметическое распределения, стандартное_откл – среднее квадратическое отклонение распределения, интегральная – логическое значение, определяющее форму функции. Если интегральная имеет значение 1, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение 0, то возвращается функция плотности распределения.

Если выдвинута гипотеза о показательном (экспоненциальном) распределении, то удобно пользоваться встроенной функцией = ЭКСПРАСП (x; лямбда; интегральная), где x – это значение функции, лямбда – это значение параметра, интегральная – это логическое значение, которое указывает, какую форму экспоненциальной функции использовать. Если интегральная имеет значение 1, то функция ЭКСПРАСП возвращает интегральную функцию распределения; если этот параметр имеет значение 0, то возвращается функция плотности распределения.

В результате выполненных расчетов получим: = 221,0; D* = 152,0; * = 12,329.

Для построения графиков надо:

• построить гистограмму и нормальную кривую по алгоритму, приведенному в лабораторной работе №4 (задание №2);

• для нанесения кривых экспоненциального и равномерного законов на график надо выделить диапазон H1:I7, зацепить его мышкой и перетащить на диаграмму;

	А	В	С	D	E	F	G	H	I
1	ai		mi*	f *	mi*	2mi*	Нормальный	Экспоненциальный	Равномерный
2	190	=(A2+ A3) /2	7	=C2 / $C$8 / 10	=B2*C2	=B2^2* C2	=НОРМРАСП (B3;$B$9;$F$9;1)– НОРМРАСП (B2;$B$9;$F$9;1)	=ЭКСПРАСП (B3;1/$B$9;1)– ЭКСПРАСП (B2;1/$B$9;1)	=(B3–B2) / ($D$10–$B$10)
3	200		14
4	210		38
5	220		62
6	230		54
7	240		25
8	250		=СУММ (C2:C7)		=СУММ (E2:E7)	=СУММ (F2:F7)
9		=E8/ C8	D*	=F8/C8–B9^2	*	=КОРЕНЬ (D9)
10	а*	=В9–КОРЕНЬ(3)*F9	b*	=В9 + КОРЕНЬ (3)*F9

Р и с. 25

• на диаграмме появятся соответствующие графики, но нормальная кривая преобразуется в ступенчатый график. Для изменения вида графика надо щелкнуть по нему левой мышкой, правой мышкой вызвать контекстное меню и выбрать Тип диаграммы…/ Стандартные / График с маркерами, помечающими точки данных / ОК;

• в результате выполненных действий получатся графики, приведенные на рис. 26.

Анализ графиков позволяет сделать вывод, что рассматриваемое распределение явно не экспоненциальное.

Для проверки гипотез о нормальном или равномерном распределениях рассчитаем теоретические частоты и наблюдаемые значения по критерию Пирсона. Все расчетные формулы приведены на рис. 27.

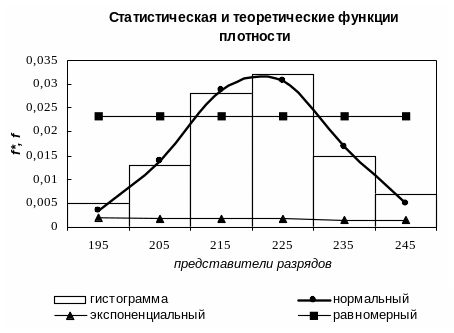
Р и с. 26

	J	K	L	M
1	m (норм.)	m (равномер.)	(норм.)	(равномер.)
2	=G2* 10 *$C$8	=I 2* 10* $C$8	=(J2 – C2)^2 / J2	=(K2 – C2)^2 / K2
3
4
5
6
7
8	=СУММ(J2:J7)	=	=СУММ(L2:L7)	=СУММ(M2:M7)
9		=	=ХИ2ОБР(0,05;4)

Р и с. 27

В результате выполненных расчетов получили (норм.) = 2,908; (равномер.) = 31,090; _{0,05; 4}= 9,488.

Итак, (норм.) < _{0,05; 4}, (равномер.) > _{0,05; 4}, следовательно, нет оснований отвергать нулевую гипотезу о нормальном законе распределения генеральной совокупности. Гипотеза о равномерном распределении отвергается. 

Задание № 2. На основании исходных данных, приведенных ниже, выдвинуть и проверить гипотезу при уровне значимости  = 0,05 о виде закона распределения. Рассмотреть нормальный, экспоненциальный и равномерный законы.

Вариант №1. На сортировочной станции в течение дня регистрировали время, затраченное на расформирование составов, и получили эмпирическое распределение, приведенное в таблице.

Границы интервала в час.	0– 0,1	0,1–0,2	0,2–0,3	0,3–0,4	0,4–0,5	0,5–0,6	0,6–0,7	0,7–0,8	0,8–0,9	0,9–1,0
Количество составов	11	14	22	27	32	29	22	20	14	9

Вариант №2. В таблице приведены значения удельного веса прочих грузов (в %) в общем грузообороте железных дорог.

Удельный вес прочих грузов (в %)	35,5–36,5	36,5–37,5	37,5–38,5	38,5–39,5	39,5–40,5	40,5–41,5	41,5–42,5	42,5–43,5	43,5–44,5
Частота	1	2	3	5	10	13	9	6	1

Вариант №3. В вагонном депо был проведен анализ суточного расхода материала А за 150 наугад отобранных рабочих дней.

Суточный расход материала (в единицах)	1–2	2–3	3–4	4–5	5–6	6–7	7–8	8–9	9–10
Число дней с данным расходом	16	15	17	18	18	11	16	19	20

Вариант №4. В вагонном депо был проведен анализ расхода деталей А при ремонте четырехосных полувагонов. Анализом было охвачено 120 наугад выбранных отремонтированных полувагонов.

Расход деталей (в шт.) на один полувагон	4 – 6	6 – 8	8 –10	10–12	12–14	14–16	16–18	18–20
Количество полувагонов	5	12	15	22	18	14	22	12

Вариант №5. В таблице приведены данные о расходе электроэнергии электровозом (в кВт ч / 10 тыс. ткм брутто), следующим во главе поезда по участкам железной дороги.

Расход электроэнергии	Количество электровозов	Расход электроэнергии	Количество электровозов
3,1–3,3	1	4,1–4,3	64
3,3–3,5	5	4,3–4,5	38
3,5–3,7	10	4,5–4,7	16
3,7–3,9	14	4,7–4,9	6
3,9–4,1	45	4,9–5,1	1

Вариант №6. В таблице приведены результаты 100 измерений внутреннего диаметра подшипника

Границы интервала	50,1–50,15	50,15–50,2	50,2–50,25	50,25–50,3	50,3–50,35	50,35–50,4	50,4–50,45	50,45–50,5	50,5–50,55
Частота	10	33	5	15	9	10	10	19	9

Вариант №7. В таблице приведены значения расчетной фондоемкости (в руб. / 10 ткм) для 100 участков железной дороги

Фондоемкость	9,8–10,6	10,6–11,4	11,4–12,2	12,2–13	13–13,8	13,8–14,6	14,6–15,4	15,4–16,2
Количество участков	4	10	19	27	24	10	4	2

Вариант №8. На складе железной дороги была проведена регистрация данных о продолжительности выгрузки материалов из прибывающих на склад автомашин.

Продолжительность выгрузки (в мин.)	0 –20	20–40	40–60	60–80	80–100	100–120	100–140
Частота	133	45	15	4	2	1	2

Вариант №9. В конце смены выборочно сделаны замеры длины 80 валов. Результаты замеров представлены в таблице.

Интервал измерения, мм	90,24–90,28	90,28–90,32	90,32–90,36	90,36–90,40	90,40–90,44
Число	5	18	32	12	13

Вариант №10. В табл. приведены результаты выборочного обследования 100 рабочих депо, проведенного с целью определения времени, затрачиваемого на обработку детали.

Время обработки, мин.	3,6–4,2	4,2–4,8	4,8–5,4	5,4–6,0	6,0–6,6
Число рабочих	14	33	35	12	6