Зведена таблиця для f- автомата Мура.

При іншому способі задання скінченого автомата використовується поняття направленого графа. Граф автомата представляє собою набір вершин, які відповідають різним станам автомата і з’єднуючих вершини дуг графа, які відповідають тим чи іншим переходам автомата. Якщо вхідний сигнал х_к викликає перехід із стану z_i в стан z_j, то на графі автомата дуга, яка з’єднує вершину z_i позначається x_k. Для того, щоби задати функцію виходів дуги графа необхідно відмітити відповідними вихідними сигналами.     Для автоматів Мілі ця розмітка відбувається наступним чином. Якщо вхідний сигнал х_к діє на стан z_i, то, згідно сказаному вище, отримується дуга, яка виходить з z_i і помічається х_к. Цю дугу додатково відмічають вихідним сигналом y= ψ(z_i,x_k).     Для автомата Мура ця розмітка така. Якщо вхідний сигнал х_к, який діє на деякий стан автомата, викликає перехід в стан z_j, то дугу, яка направлена в z_j і помічену х_к додатково відмічають вихідним сигналом y= ψ(z_j,x_k).

Розглянемо приклади представлення графом.

F-автомат Мілі.

Таблиця переходів

Таблиця виходів

F-автомат Мура

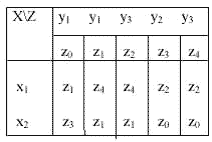
При рішенні задач моделювання систем часто зручнішою формою є матричне задання. При цьому матриця C=||Cij||, стрічки якої відповідають біжучим станам, а стовбці - станам переходу, містить елементи ci,j =xk/ys, де xk - вхідний сигнал, ys - вихідний сигнал.     Для F-автомата Мілі відповідна матриця буде виглядати наступним чином:

Якщо перехід із стану zi в стан zj відбувається під впливом декількох сигналів, елемент матриці ci,j представляє собою множину пар вхід-вихід для цього переходу, які з’єднані знаком диз’юнкції “V”. Для F- автомата Мура елемент ci,j дорівнює множині вхідних сигналів на переході zi - zj, а вихід описується вектором виходів:

i-та компонента якого - вихідний сигнал, який відповідає стану z_i.

Для розглянутого F- автомата Мура матриця з’єднань і вектор виходів має вигляд:

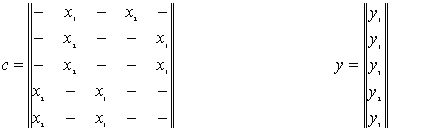
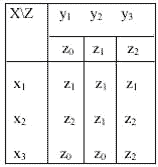
Для детермінованих автоматів виконується умова однозначності переходів, тобто автомат, який знаходиться в деякому стані, під дією будь-якого вхідного сигналу не може перейти в більш ніж в один стан. Стосовно до графічного опису F- автомата, це означає, що на графі автомата з будь-якої вершини не можуть виходити два і більше ребра, помічених одним і тим самим вхідним сигналом. Розглянемо вид таблиці переходів і граф асинхронного скінченого автомата. Для F- автомата стан zk називається стійким, якщо для будь-якого вхідного сигналу xi, для якого виконується умова φ(zk,xi)=zk, існує ψ(zk,xi)=yk. Таким чином F- автомат називається асинхронним, якщо кожен його стан zk, який належить множині z, є стійким.

Асинхронний F- автомат Мура.

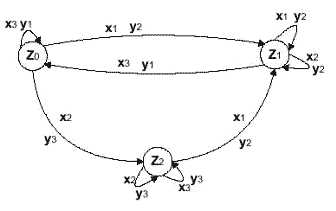
В якості об’єктів, які описуються F-автоматами можна назвати елементи і вузли ЕОМ, пристрої контролю, регулювання і управління. Для всіх цих об’єктів характерними є дискретний характер роботи у часі.

Лекція 5. Дискретно-стохастичні моделі (р-схеми).

Розглянемо даний підхід на прикладі ймовірнісних автоматів. Ймовірнісний автомат можна визначити як дискретний потактовий перетворювач інформації з пам’ятю, функціонування якого в кожному такті залежить тільки від стану пам’яті і може бути описане статистично. Введемо визначення Р-автомата, використовуючи поняття F-автомата.

Розглянемо множину G, яка представляє собою елементи (zk,zi), де zk – стан, zk Є Z; xi – вхідний сигнал, xi Є X.

Якщо існують функції φ(zk,xi) і ψ(zk,xi), які відображають множину G відповідно на множини Z і Y (G→Z і G→Y), то говорять, що заданий F-автомат F<Z, X, Y, φ, ψ >.

В більш загальному виді математичну схему Р-автомата можна представити наступним чином.

Нехай крім множини G задана множина Ф(zk,yj). Тоді якщо існує відображення множини G на множину F у вигляді закону розподілу для кожного елемента (zk,xi), то говорять, що заданий ймовірнісний Р-автомат.

Цей закон розподілу можна представити у вигляді таблиці:

j - кількість вихідних сигналів.

Приклад.

Х={x1, x2}

Z={z0, z1, z2}

Y={y1, y2}

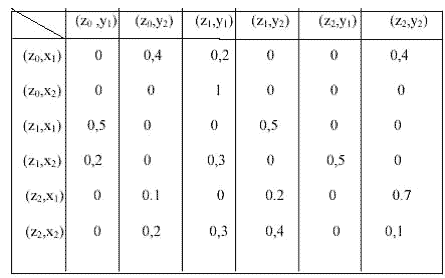
Кількість таких розподілів дорівнює кількості елементів множини G. Тому ймовірнісний автомат P можна представити як P<Z, X, Y, B>. В- сукупність розподілів.

Нехай елементи множини G визначають деякі закони розподілу на підмножини Y, Z.

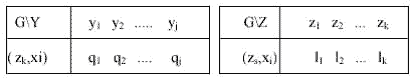
- умови нормування.

Якщо для всіх значень l і q виконується умова l_kq_j=b_kj, то такий ймовірнісний автомат називається ймовірнісним автоматом Мілі. Ця вимога означає виконання умови незалежності розподілів для нового стану Р-автомата і його вихідного сигналу.

Нехай тепер значення вихідного сигналу Р-автомата залежить тільки від стану, в якому знаходиться автомат в даний момент часу.

Якщо для будь-якого к і j виконується l_ksj=b_kj, то такий ймовірнісний автомат називається автоматом Мура.

Якщо вихідний сигнал P-автомата визначається детерміновано, то такий автомат називається Y- детермінованим P- автоматом.

Z- детермінованим ймовірнісним автоматом називається Р- автомат, у якого вибір нового стану є детермінованим.

Розглянемо Y-детермінований Р-автомат, який задається таблицею переходів Р і таблицею виходів.

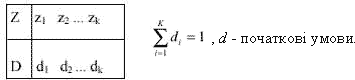
Будемо вважати, що до початку роботи Р-автомат завжди знаходиться в стані z0 і в нульовий такт часу міняє стан у відповідності з розподілом D. Інформацію про початковий стан зручно внести в матрицю Р змінивши її розмірність до (к+1) (к+1). Перша стрічка, яка буде співставлятися з z0 буде мати вигляд: 0, d1, d2, ... , dk, а перший стовбець буде нульовим. Описаний Y-детермінований Р-автомат можна задавати у вигляді орієнтованого графа, вершини якого співставляються станам автомата, а дуги - можливим переходам з одного стану в другий. Дуги мають вагу, яка відповідає ймовірності переходу pij. Біля вершин графа записуються значення вихідних сигналів, які викликаються цими станами. Задання Y-детермінованого Р-автомата еквівалентне заданню деякого дискретного марківського ланцюга із скінченою множиною станів. Тому апарат марківських ланцюгів є основним для використання Р-схем для аналітичних розрахунків.

Розглянемо приклад Y- детермінованого P - автомата.

Вимагається оцінити суму фінальних ймовірностей перебування автомата в станах z2 і z3, в яких на виході автомата видається одиничний вихідний сигнал.

Оскільки фінальні ймовірності не залежать від стану z0, то ймовірність знаходження в станах z1, z2, z3, z4 можна знайти з матричного рівняння:

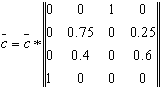
де c=(c1, c2, c3, c4)

c₁=c₄ c₂=0.75c₂ + 0.4c₃ c₃=c₁ c₄=0.25c₂ + 0.6c₃ c₁+c₂+c₃+c₄=1 - умова нормування. c₂=8/23, c₃=5/23, c₂+c₃=13/23.

Для оцінки різних характеристик досліджуваних систем, які представляються у вигляді Р - схем, крім аналітичних моделей можна застосувати і імітаційні моделі.