1

Для сокращения сроков сертификации и летных испытанный в последнее время все больший объем работы переводится на наземные стенды в качестве одного из таких стендов используется реальный самолет, на котором идет подготовка к первому полету.

2

1. Системы координат

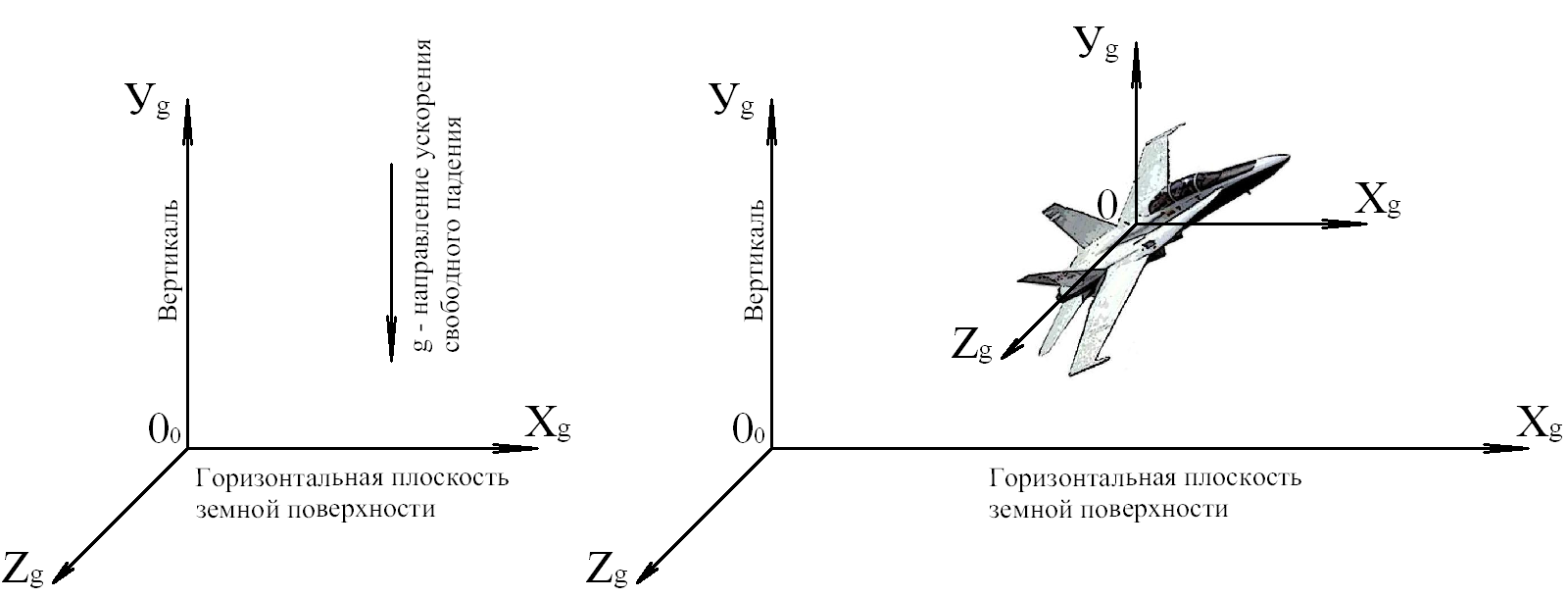
   1. Нормальная земная система координат

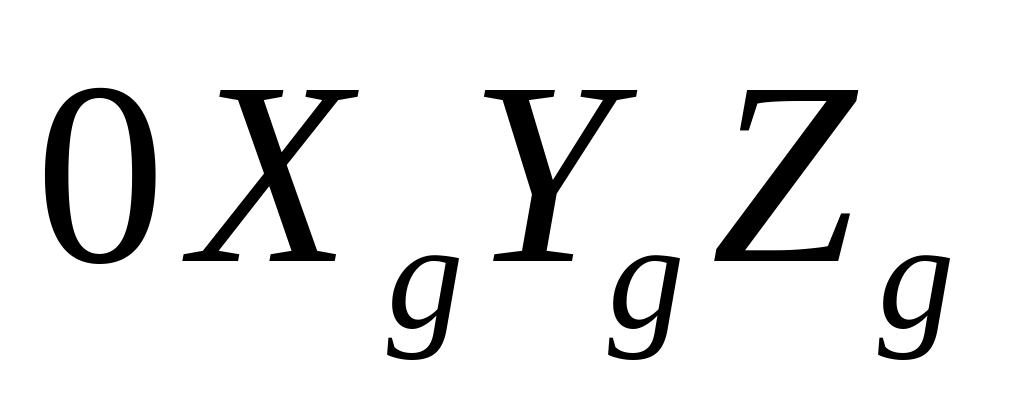
Система координат (рис. ), начало которой фиксировано по отношению к Земле, ось направлена по местной вертикали вверх, а направления осей и выбираются в соответствии с задачей.

3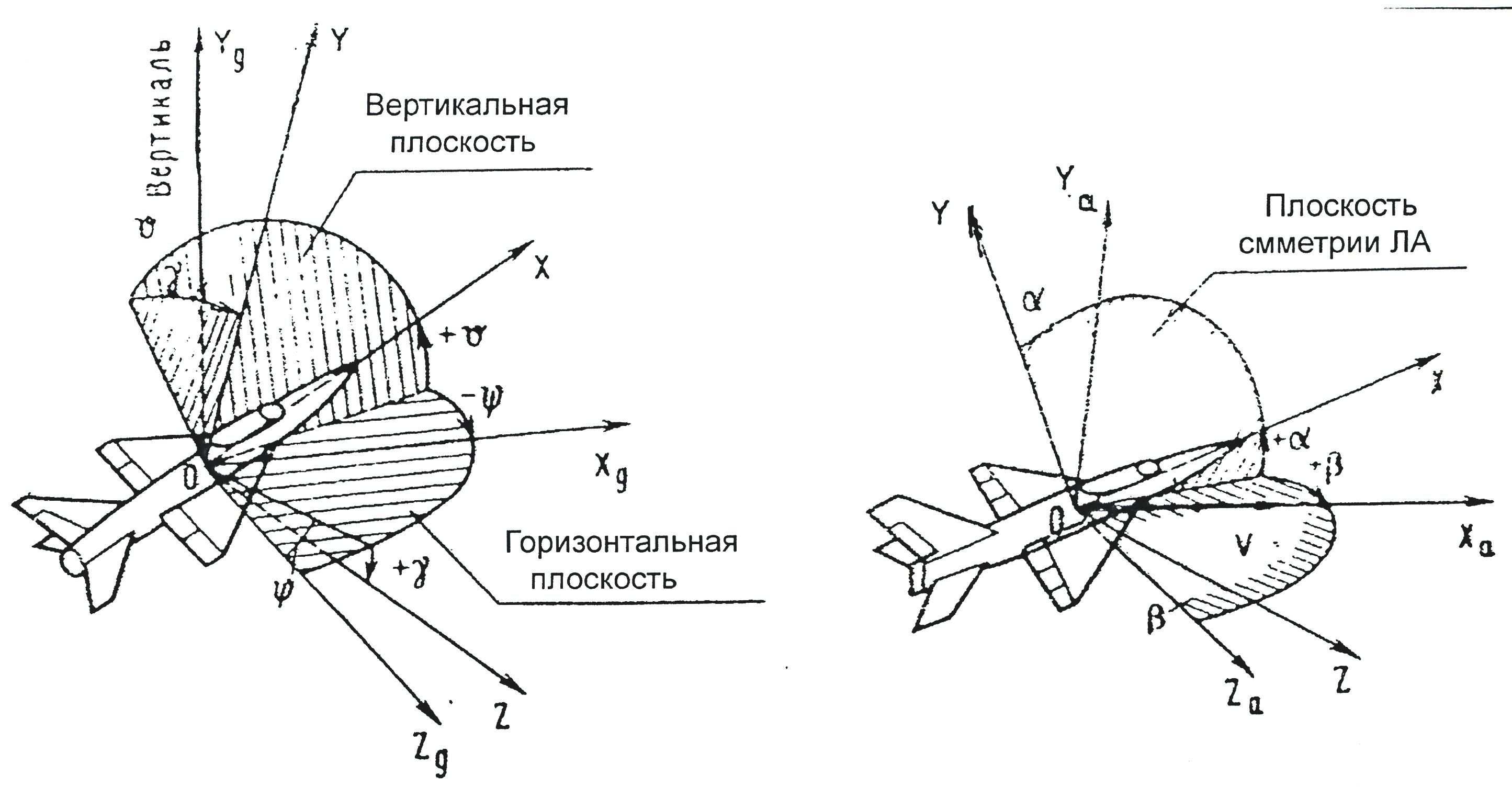

Рис. Связанная система координат и углы между осями связанной и нормальной систем координат, определяющие положение ЛА относительно земной поверхности.

Рис.1.4. Скоростная система координат и углы между скоростной и связанной системами координат, определяющие положение ЛА относительно вектора воздушной скорости ЛА.

1 4 .2 Скоростная система координат

Система координат (рис. 4), начало которой О помещено в центре масс ЛА, ось совпадает по направлению с вектором скорости, ось расположена в плоскости симметрии ЛА и направлена к верхней его части. Ось перпендикулярна плоскости .

Углы, определяющие положение летательного аппарата относительно вектора скорости

Угол атаки α - угол между связанной осью и проекцией вектора скорости на плоскость симметрии ЛА.

Угол скольжения β - угол между вектором скорости и плоскостью симметрии ЛА. Знаки углов атаки и скольжения определены на рис. 4.

Углы, определяющие положение летательного аппарата относительно Земли

По определению нормальной и связанной систем координат положение ЛА относительно Земли определяется углами между осями связанной и нормальной системы координат.

Угол тангажа υ – угол между связанной осью и горизонтальной плоскостью ;

Угол рыскания ψ – угол между осью и проекцией связанной оси на горизонтальную плоскость ;

У

5

гол крена γ – угол между связанной осью и осью смещенной в положение, соответствующее нулевому углу рыскания.

Знаки углов определены на рис. 3.

Воздушная скорость летательного аппарата – скорость центра масс (начала О связанной системы координат) относительно воздушной среды, не возмущенной летательным аппаратом.

Земная скорость летательного аппарата – скорость центра масс (начала О связанной системы координат) относительно выбранной земной системы координат.

Путевая скорость летательного аппарата – проекция земной скорости летательного аппарата на горизонтальную плоскость.

Траекторные углы

Угол пути ψ – угол между осью и путевой скоростью летательного аппарата (рис.5)

В продольном движении центра масс на самолет как на любое тело, действуют четыре силы, условно приложенные в центре масс. Эти силы фактически являются суммой сил, действующих на различные элементы самолета.

1

6

. Сила тяжести (земная система координат)

2. Подъемная сила (скоростная с-ма координат)

3. Сила сопротивления (скорост. с-ма координат)

4. Сила тяги двигателей (связанная система)

- режим работы двигателей.

2. Система уравнений движения

Уравнения движения записываются в проекциях на скоростную систему координат

Поскольку , равно центростремительному ускорению

- мал, - мал, то уравнения (1), (2) можно переписать в виде:

Для определения ЛТХ нужно добавить переход от скоростной системы к земной, а также отдельное уравнение для расхода топлива.

7

Получим систему из дифференциальных уравнений (опуская индекс «а», т.е. , ):

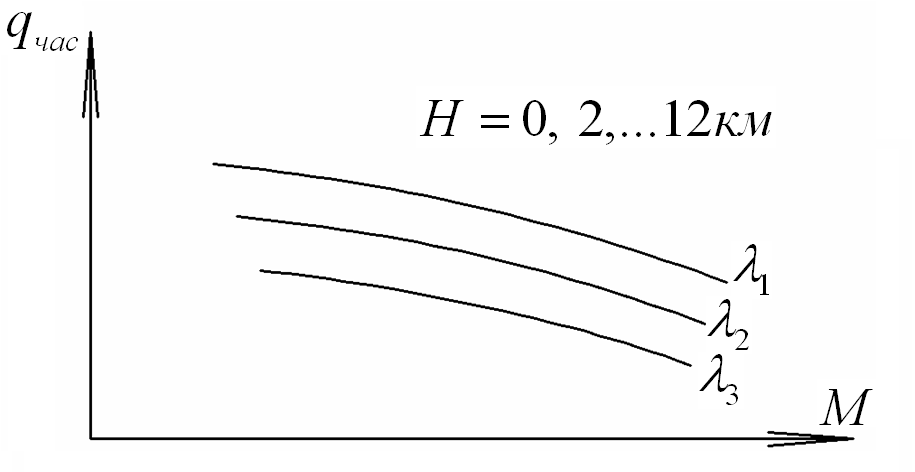
- секундный расход топлива двигателя, задается в виде:

,

- данные моторного завода.

Из решения уравнений (1)-(6) можно найти показатели ЛТХ: .

Эти уравнения решаются, как правило, методами численного интегрирования, для чего необходимо записать еще ряд аналитических и графических зависимостей:

8
- стандартная атмосфера
- стандартная атмосфера, скорость звука

8А

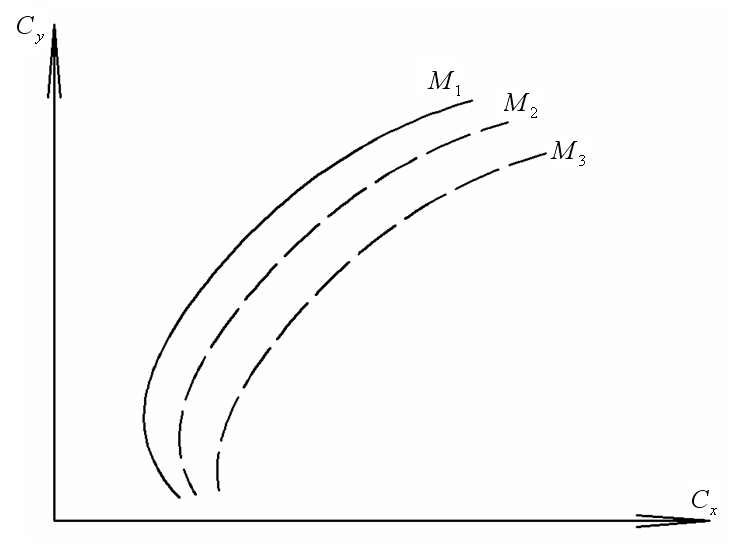
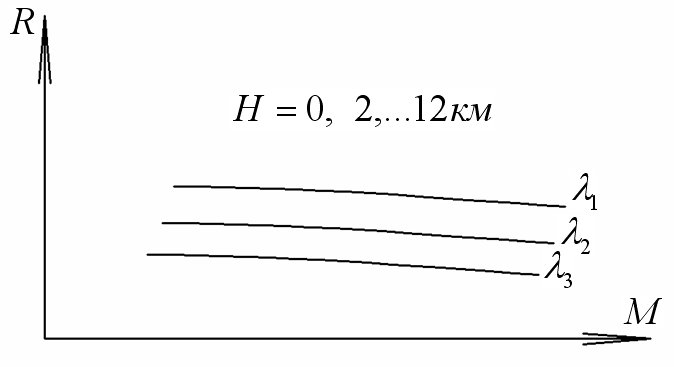
Система уравнений (1) – (13) содержит 15 неизвестных, т.е. две неизвестных должны быть заданы и называются управлениями. Для типового профиля полета задаются:

1. В

   9

   злет: , .

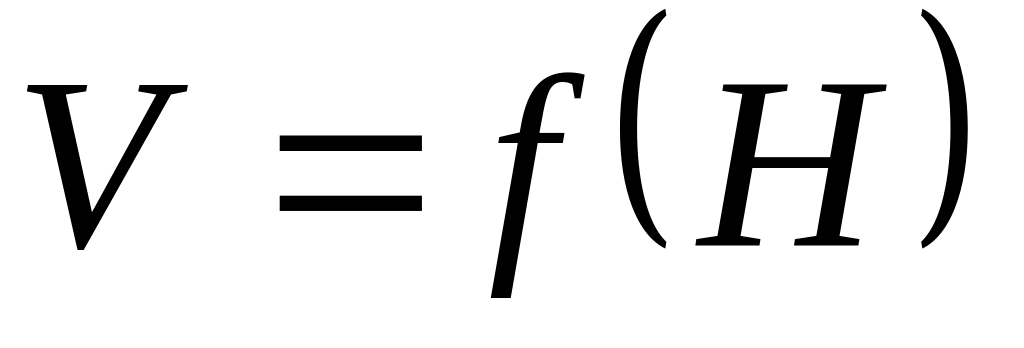2. Набор высоты: , .

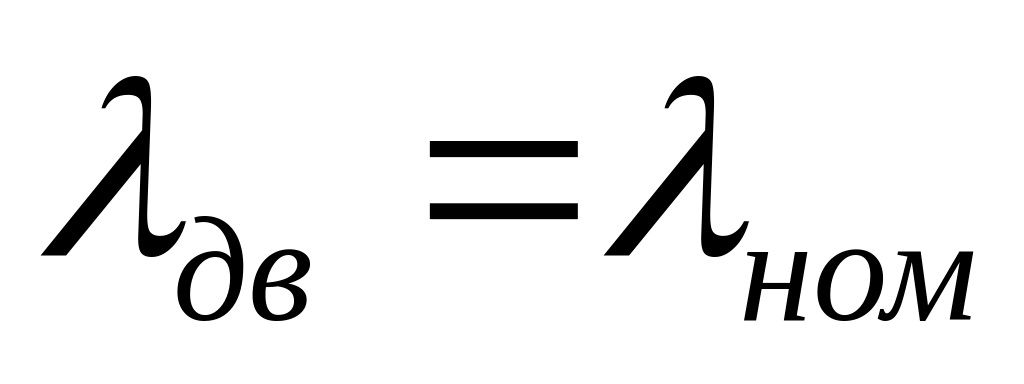3. Крейсерский полет: а.) , ,

б.) , .

4. Снижение (планирование): , .

5. Заход на посадку: , .

На предварительных этапах проектирования система уравнений (1) – (13) обычно решается приближенными методами. Для этого вводятся допущения для режимов 2, 3, 4: , . Параметры скорость и угол наклона траектории меняются медленно для транспортных магистральных самолетов. Кроме того, в ряде случаев можно считать, что угол мал, т.е. , .