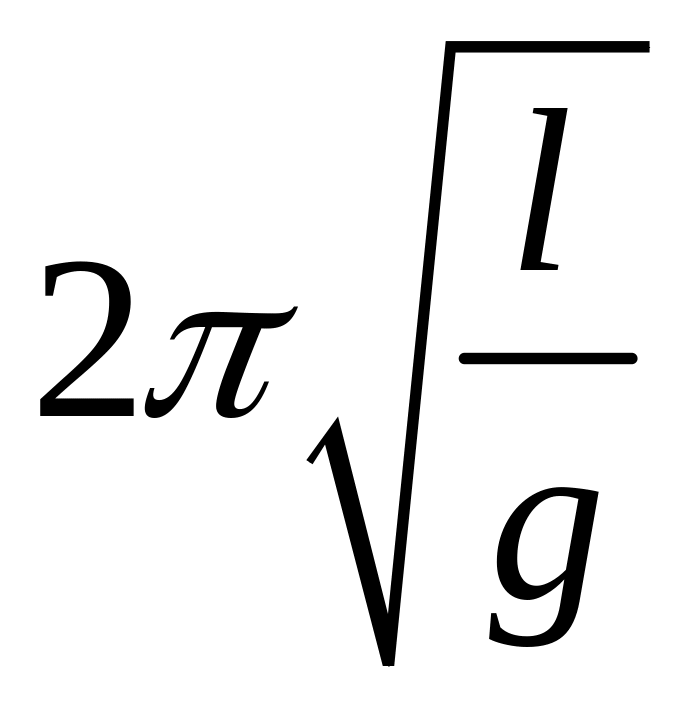Работа 6.1.2. Математический маятник

Порядок выполнения работы.

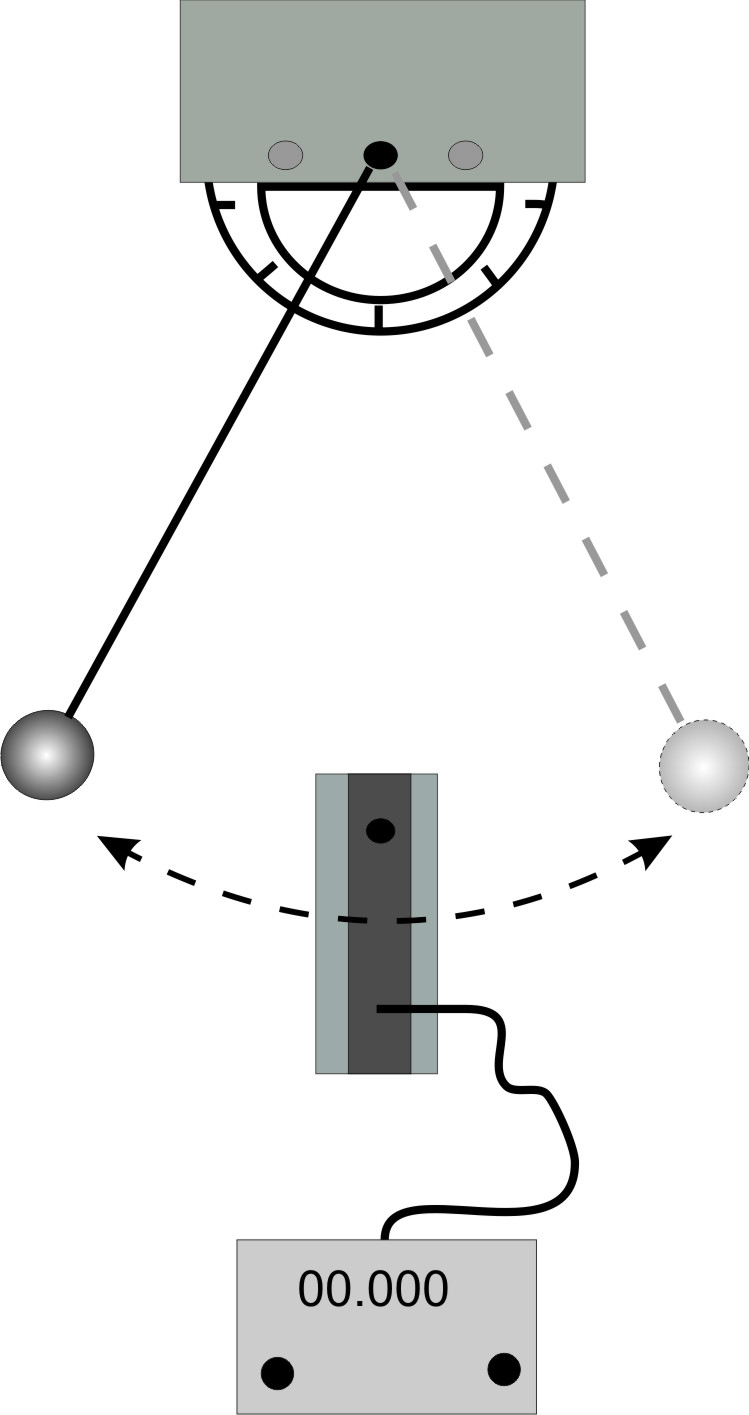
1. Установка для выполнения опыта схематически изображена на рисунке.

2. Для экспериментального исследования законов колебаний математического маятника разместите на металлической классной доске магнитную плату держателя нити и оптоэлектрический датчик.

3. Подключите оптоэлектрический датчик к гнезду 1 на задней панели цифрового секундомера. Включите прибор и переключите секундомер в режим (г ).) измерения периода колебаний.

4. Закрепите нить математического маятника на плате держателя в вертикальном положении.

5. Убедитесь, что стальной шарик маятника свободно проходит через створ оптического датчика.

6. Выведите маятник из положения устойчивого равновесия, отклонив нить от вертикали, отпустите маятник и не менее трех раз измерьте период колебаний маятника при различных значениях амплитуды колебаний. Убедитесь, что для углов 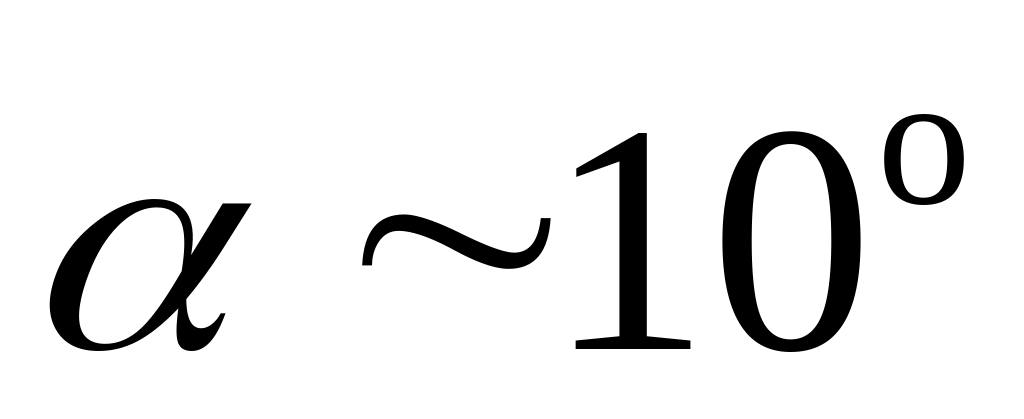, период Т колебаний при неизменных массе и длине нити не зависит от амплитуды А колебаний.

7. Повторите измерения периода колебаний маятника заменив стальной шарик свинцовым и убедитесь, что период Т малых колебаний математического маятника при одинаковой амплитуде (А~5-10 см) и неизменной длине нити не зависит от его массы.

8. Повторите измерения периода колебаний маятника при различных значениях длины нити, проверьте выполнимость соотношения 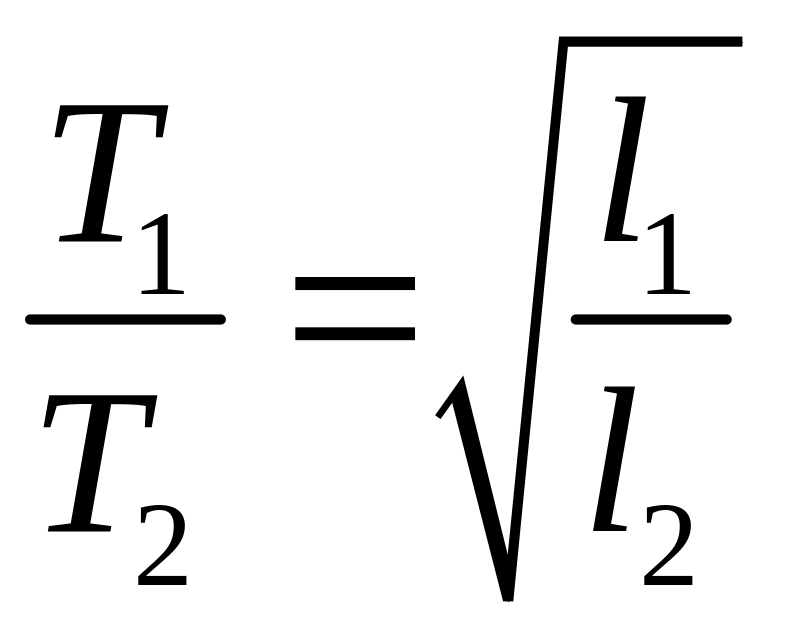и покажите, что период колебаний Т прямо пропорционален корню квадратному из длины маятника .

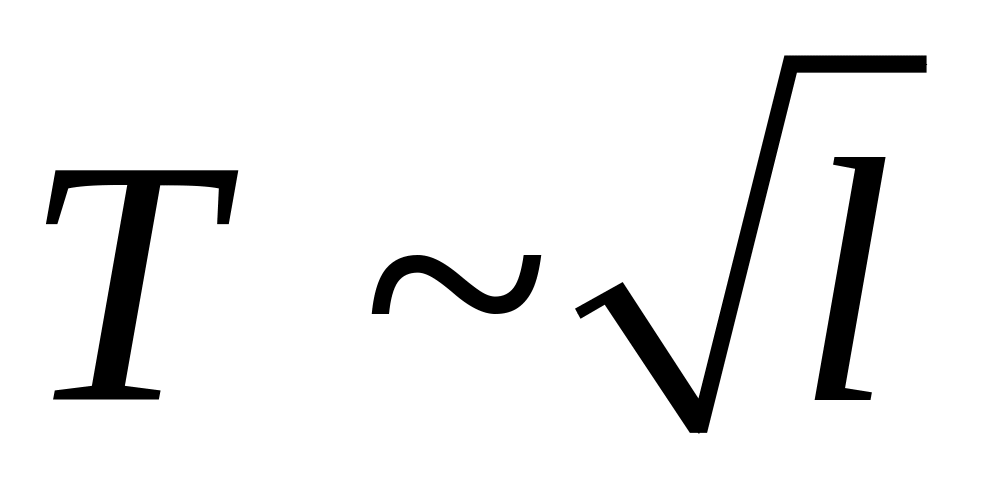9. Рассчитайте отношение экспериментально измеренного значения периода колебаний маятника к рассчитанному теоретически значению 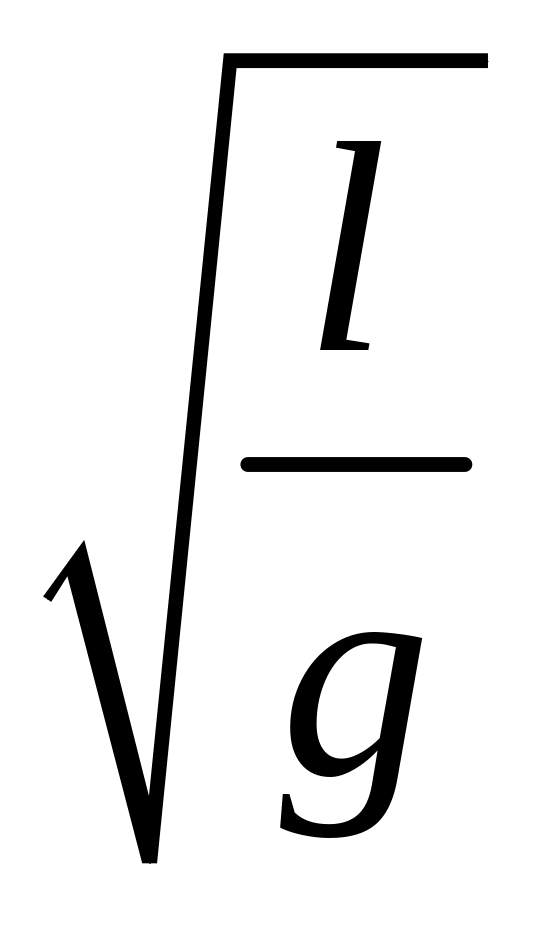и проверьте справедливость формулы .

10. Выразите g из формулы 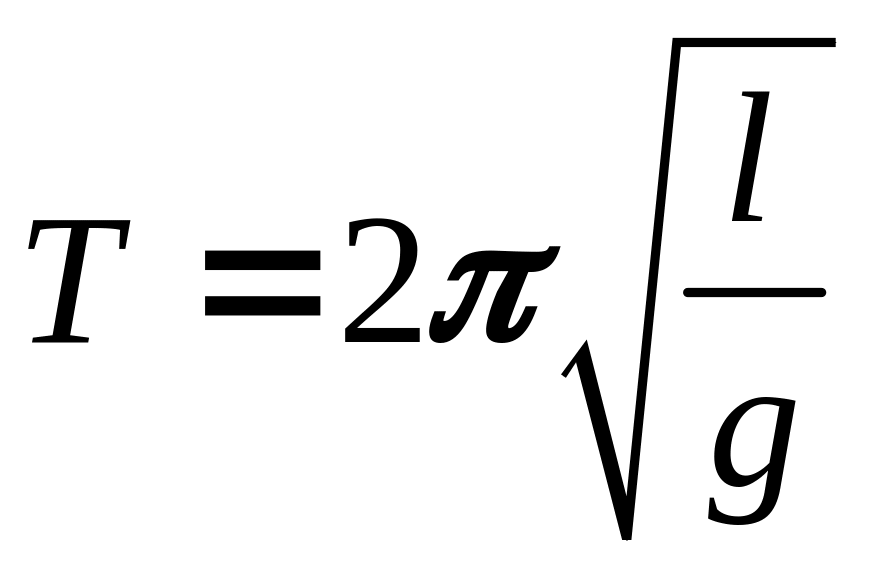и рассчитайте его значение, воспользовавшись экспериментальными результатами измерений длины и периода колебаний математического маятника. Сравните полученный результат с табличным значением g.

11. Результаты измерений и вычислений занесите в таблицу.

Таблица

Хотя эксперимент проводится на очень простом оборудовании, но оно позволяет обобщить знания о всех величинах, характеризующих колебательные процессы, проанализировать их закономерности и, кроме того, обратить внимание учащихся на условия, которые надо учитывать при выполнении опытов

6.2. Исследование зависимости характеристик математических маятников от амплитуды колебаний

Цель работы: исследование зависимости характеристик нитяных маятников от амплитуды колебаний, массы грузов, длины нити.

Оборудование: два нитяных маятника с подвесами (шариками различной массы), штатив с зажимом, метровая линейка с миллиметровыми делениями, секундомер или часы с секундной стрелкой, весы, разновес.

Вывод расчетной формулы

Периодом колебаний называется промежуток времени, в течение которого маятник совершает одно полное колебание :где п — число полных колебаний; t — время, за которое совершено п колебаний.

Маятник совершает одно колебание, проходя по дуге от одного крайнего положения до другого, и возвращается в исходную точку. Расстояние от положения равновесия маятника до одного из крайних положений называется амплитудой колебаний А.

Порядок выполнения работы

П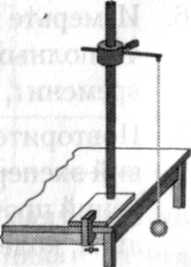 оставьте штатив на край стола так, чтобы зажим для подвеса маятника выступал за край стола (см. рис.6-1).

1. Определите с помощью весов массу m₁, шарика, который будете подвешивать на нити, не менее пяти раз. Вычислите среднее значение массы ‹ т_х›. Результаты измерений и вычислений занесите в таблицу 1. Закрепите d зажиме штатива свободный конец нити маятника таким образом, чтобы длина l, подвеса маятника (расстояние от точки подвеса до центра шарика) была не менее 1 м. Измерьте длину маятника не менее пяти раз. Вычислите среднее значение ‹l›. Результаты измерений и вычислений занесите в таблицу 1.

4. Отведите шарик в сторону от положения равновесия и осторожно отпустите его, стараясь избежать боковых толчков. Маятник начнет колебаться.