Фиг.11 Силы, действующие на закреплённую ракету.

Для закреплённой ракеты, сила тяги P уравновешивается реакцией связи R, равной тяге P.

Поэтому, ускорение , и уравнение движения для точки переменной массы (3), примет вид:

,

где S_a – площадь выходного сечения сопла;

ω_а – скорость потока в выходном сечении сопла. ω_а называется скоростью истечения.

Так как R=P, то тяга .

Следует особо подчеркнуть, что под давлением p понимается исключительно барометрическое давление окружающей среды, но не реальное распределение давления на поверхности ракеты, значение и закон распределения которого зависит от условий обтекания.

Все добавочные силы, связанные с условиями полёта ракеты в атмосфере (ориентация, возмущающие факторы, характер отрывных течений и т.д.), относятся к категории аэродинамических сил и в выражение тяги ракетного двигателя не включаются. Поскольку барометрическое давление p окружающей среды зависит от высоты h, p=f(h), то его обозначают p_h, тогда выражение для тяги ракетного двигателя на высоте h получен в следующем окончательном виде:

(5)

или

Из последних выражений следует, что для стартующей с Земли ракеты, тяга при неизменном расходе (m=const) непрерывно возрастает от своего начального значения

,

где p₀ – давление у поверхности Земли, до наибольшего значения, называемого пустотной тягой:

(6)

Отличие стартовой тяги от пустотной определяется площадью выходного сечения сопла S_a и для реальных ракетных двигателей лежит в пределах 10 – 20 %.

После того, как введено понятие тяги ракетного двигателя, мы получаем возможность записать уравнение для поступательного движения ракеты в обычной форме закона Ньютона (см.(1)).

,

где М – текущее значение массы ракеты,

– под знак суммы внесены составляющие нерассмотренных пока сил – аэродинамическое сопротивление ракеты и вес ракеты.

Итак, истекающую струю газов мы отделили от ракеты плоскостью, проходящей через выходное сечение сопла.

Но, как было сказано ранее, это не единственное решение.

В частности, разделение можно произвести по внутренней поверхности ракетного двигателя (камеры), заменив действие отброшенных газов на внутренние стенки реактивного двигателя (внутренней камеры) некоторым изменяющимся вдоль оси давлением p_г, приводящим к возникновению результирующей силы p_г (фиг.12).

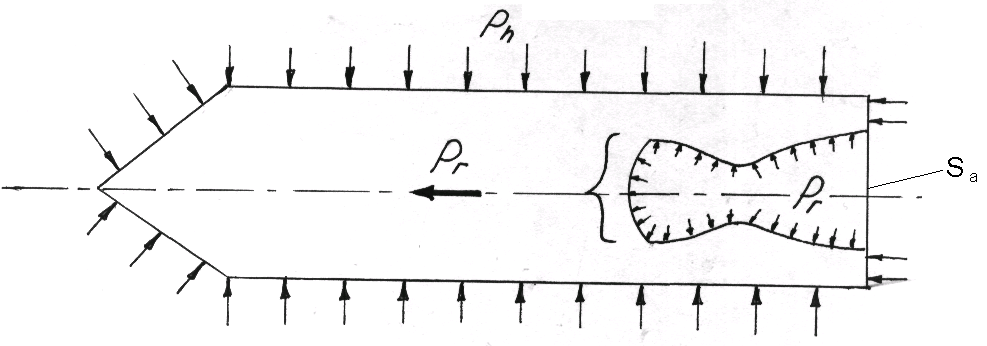
Фиг.12. Распределение сил давления по поверхности ракеты и по внутренней поверхности камеры реактивного двигателя.

Нетрудно догадаться, что результирующая сила P_г как раз и представляет собой пустотную тягу P_п.

Для определения тяги реактивного двигателя на высоте h из пустотной тяги , следует вычесть произведение , то есть:

(7)

Таким образом, мы определили, что пустотная тяга P_п представляет собой результирующую сил давления, распределённых по внутренней поверхности камеры реактивного двигателя.

В дальнейшем мы увидим, что это давление не зависит ни от скорости полёта ракеты, ни от условий окружающей среды. Поэтому, пустотная тяга P_п представляет собой одну из основных характеристик собственно самого реактивного двигателя, а не условий полёта.

Часто выражение пустотной тяги P_п записывают в форме реактивной силы

, (8)

где - эффективная скорость истечения.

Сопоставляя выражения (8) и (6), получаем:

, откуда получим:

(9)

Основной особенностью эффективной скорости истечения ω_e является то, что она не зависит от секундного расхода m, поскольку давление на выходе из сопла p_a пропорционально m, а скорость истечения ω_a также не зависит от расхода (в определённых пределах).

В реально существующих реактивных двигателях эффективная скорость истечения ω_e превышает действительную на 5 – 15 %.

В заключении можно отметить, что при выводе выражения тяги (5) нами были сделаны некоторые замаскированные упрощения:

1. Например, ускорение закреплённой на стенде ракеты мы приняли равным нулю ( =0). Между тем, центр масс ракеты вследствие сгорания топлива несколько смещается.

2. Рассматривая пустотную тягу, как равнодействующую сил p_г , мы пренебрегли тягой, создаваемой жидким топливом при впрыске в камеру.

3. Наконец, масса находящихся в камере газов должна либо включаться, либо не включаться в общую массу ракеты M.

Однако учёт перечисленных упрощений приводит к совершенно ничтожным поправкам конечного результата, и ими с полным основанием пренебрегают.