12.6. Передаточные функции и их свойства.
При исследовании
динамики летательных аппаратов как
объектов автоматического регулирования
широко используют передаточные функции
и частотные характеристики, которые
характеризуют свойства объекта
регулирования в области комплексного
переменного
и частотной области.
Уравнение возмущенного движения ракеты с «замороженными» коэффициентами в символической операторной форме можно записать в виде:
,
где
– операторные полиномы от
;
– любая из
интересующих нас величин (
и т.д.);
В дальнейшем
будем называть входной величиной, а
– выходной.
Передаточной
функцией системы
назовем отношение:
Из уравнений движения в символической операторной форме следует отношение:
,
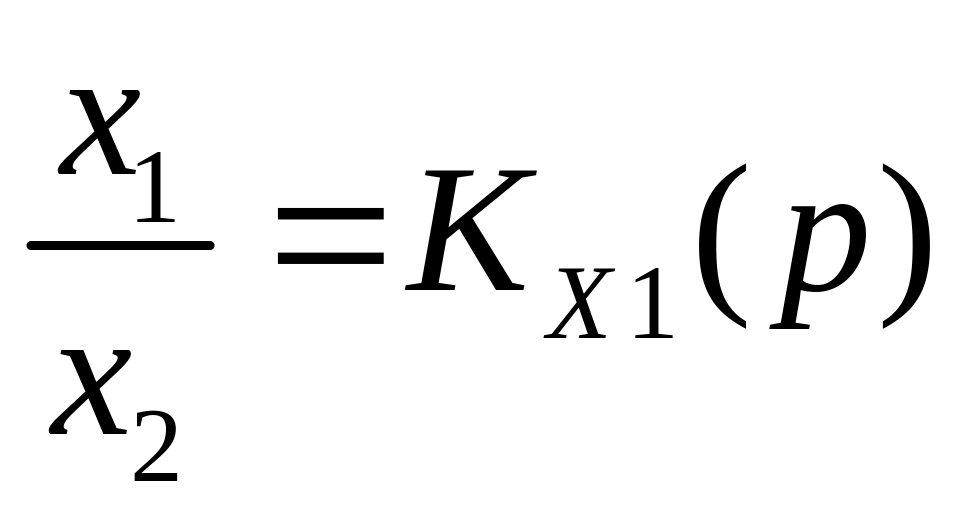которое показывает отношение результата (выходной величины) к воздействию (входной величины), выраженное в символической операторной форме.
Применяя прием “замораживания” коэффициентов, рассмотрим уравнения возмущенного движения в плоскости тангажа (193) и (195) аналогичные им уравнения в плоскости рыскания (196).
Запишем уравнения (193) в символической операторной форме:
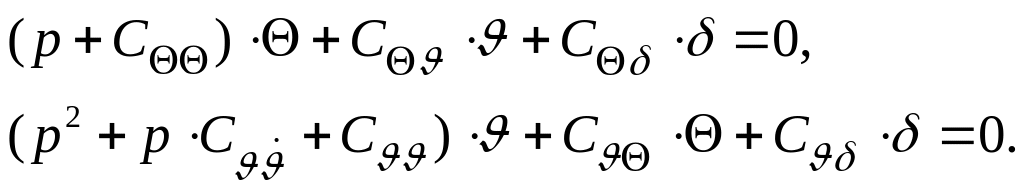(200)
Исключив ,найдем передаточную функцию:
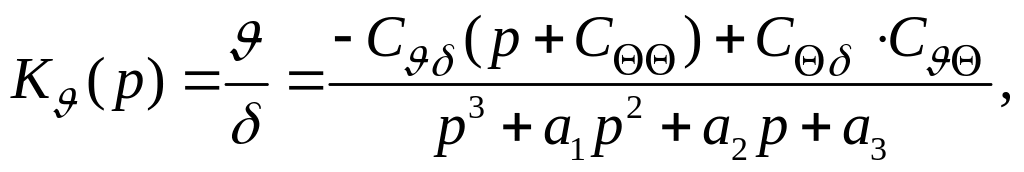(201)
в которой
(202)
Исключив из (200) ,найдем передаточную функцию:
(203)
Знаменатель передаточной функции является характеристическим полиномом систем уравнений (193) и (195):
(204)
Для системы
уравнений (196), описывающих возмущенное
движение в плоскости рыскания, коэффициент
,
так что
(205)
Корнями этого полинома будут
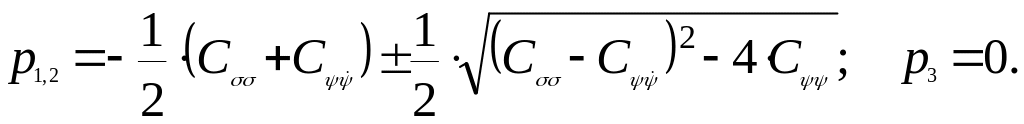
При упрощении
уравнений (190)
степень характеристического уравнения
понизилась на единицу, поэтому вместо
пары комплексно сопряженных корней,
характеризующих длиннопериодическое
движение, появился один нулевой корень.
Благодаря нулевому корню отклонения
и
в возмущенном движении, описываемом
уравнениями (196)
при
,
не затухают.
В зависимости от
знака коэффициента
корни
и
могут быть
вещественными или комплексно–сопряженными
с отрицательными вещественными частями.
Если ракета
статически устойчива (
)
и если еще
,
то
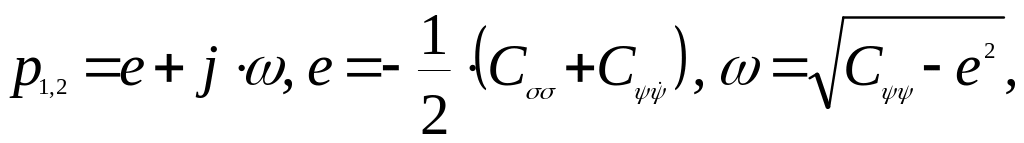(206)
где
– собственная частота угловых колебаний
статически устойчивой ракеты в потоке
воздуха.
Если ракеты
статически неустойчива (
),
то корни
и
будут вещественными,
причем
(207)
Величины и являются, кроме того, корнями знаменателя передаточных функций, найденных из уравнений (196):
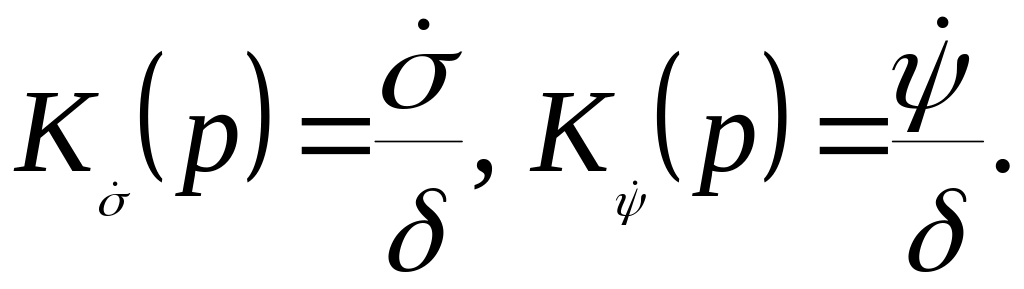
Поэтому для
статически устойчивой ракеты переходный
процесс относительно скоростей
и
колебательный и затухающий, а для
статически неустойчивой – переходный
процесс характеризуется неустойчивостью
апериодического характера.
Когда
,
то
,
движение относительно
скоростей
и
устойчиво(отклонения скоростей
и
затухают). Когда
,
то корни
и
будут вещественными, отрицательными и
равными. Свободное движение ракеты
относительно скоростей
и
также устойчиво.
Рассмотрим свойства
характеристического полинома (204).
Если
,
то
.
(208)
При заданных
начальных условиях свободное движение
(переходный процесс) относительно
координат
и
незатухающее, а относительно скоростей
и
оно затухает апериодически.
Когда центр давления
аэродинамических сил не совпадает с
центром массы ракеты
,
при анализе коэффициентов полинома
(204) возникает
два основных варианта:
а) если
,
то
и полином (204)
будет иметь один действительный
положительный корень и два
комплексно–сопряженных корней с
отрицательной вещественной частью:
;
(209)
б) если
,
то
и все 3 корня полинома (204)
вещественные, причем 2 из них положительные,
а один отрицательный:
;
(210)
Таким образом,
свободное движение в плоскости тангажа
при
неустойчиво.