12.3. Атмосферный участок (входа в атмосферу).

Раздел изучается самостоятельно. Можно использовать источник: Феодосьев В.И.“Основы техники”- “Наука”,1989г. (стр. 330-344).

12.4. Уравнения возмущенного движения.

Как уже отмечалось, действительное движение всегда будет отличаться от программного. Причины, вызывающие отклонение движения от программного, будем называть возмущающими факторами. Эти факторы могут быть как постоянными, так и случайными.

Искажение внешней геометрии корпуса ракеты, несоосность двигательной установки с корпусом, отклонения от расчетных значений тяги двигательной установки и стартового веса, изменение эффективности органов управления ракеты и другие факторы действуют постоянно и являются для конкретной заданной ракеты систематически действующими возмущающими факторами. Эти возмущения могут быть учтены в уравнениях (171) членами для разных ракет могут быть различными, то действительные траектории и параметры движения на управляемом участке будут заключены в трубку, осью которой является программная траектория.

Движение ракеты в трубке траекторий называется номинальным движением. По характеристикам возмущений можно установить размеры трубки траекторий, которые являются исходными для расчета рассеивания.

Кратковременные возмущения (порывы ветра, кратковременные изменения тяги двигательной установки, помехи и ложные сигналы в Системе Управления) обычно случайны и их невозможно учесть в уравнениях движения, хотя они оказывают порой значительное влияние на движение ракеты. Это обусловлено тем, что величина и время действия этих случайных факторов неизвестны.

Под действием этих случайных возмущений изменяются параметры движения, поэтому величину любого из них можно представить состоящей из номинального значения и малого отклонения, называемого возмущением.

(178)

Уравнения (171) (172) справедливы для произвольных функций , в частности, они справедливы и для функций номинального движения .

Обычно при линеаризации уравнений движения пренебрегают влиянием приращения высоты на аэродинамические силы и моменты, а также на силу тяги двигательной установки, т.к. это влияние за малый промежуток времени незначительно.

Значения переменных из уравнений (178) подставим в уравнения (171) и из полученного результата вычтем уравнения (171) , соответствующие параметрам номинального движения.

Примем, что .

Полагая, что возмущения и являются малыми и оставляя только члены первого порядка малости, получим следующие уравнения в скоростной системе координат относительно возмущений:

,

(где – градиент управляющей силы рулей)

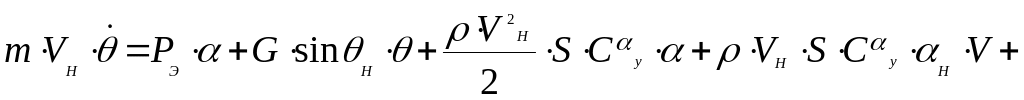
, (179)

,

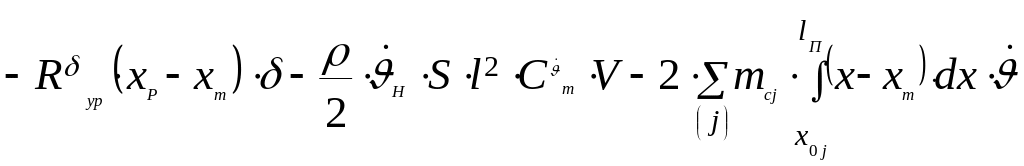где – производные от коэффициентов аэродинамических моментов по углу атаки;

– производные от коэффициентов аэродинамических демпфирующих моментов;

– расстояние от вершины ракеты до среза сопла двигательной установки;

– секундный массовый расход из j–го бака;

– расстояние от вершины ракеты до поверхности жидкости в j–м баке.

В уравнениях (179) неизвестными являются возмущения параметров движения и .

Функции и , характеризующие номинальное движение, считаем известными, их можно определить из решения уравнений (171) и (173). Т.к. номинальное движение мало отличается от программного, то в уравнениях (179) вместо номинальных значений можно принять программные значения и известные из расчета программного движения.

Тогда уравнения (179) запишем в виде:

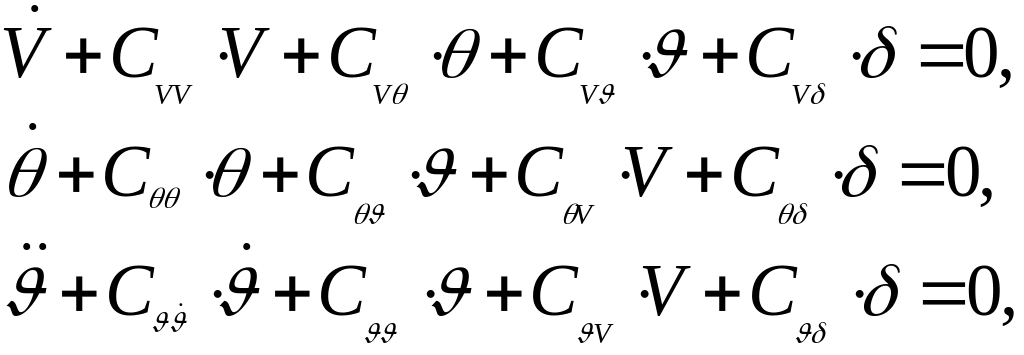(180)

Здесь введены следующие обозначения коэффициентов:

В первом уравнении

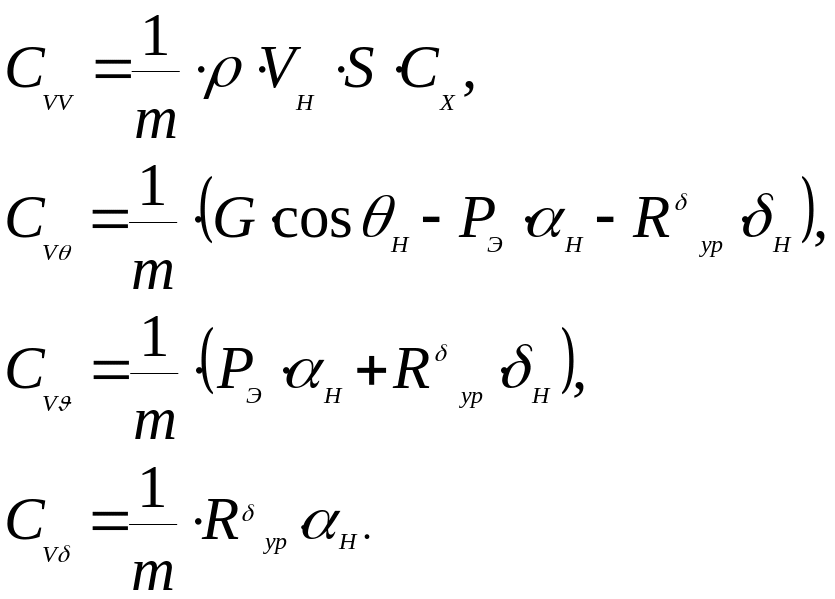(181)

Во втором и третьем уравнениях

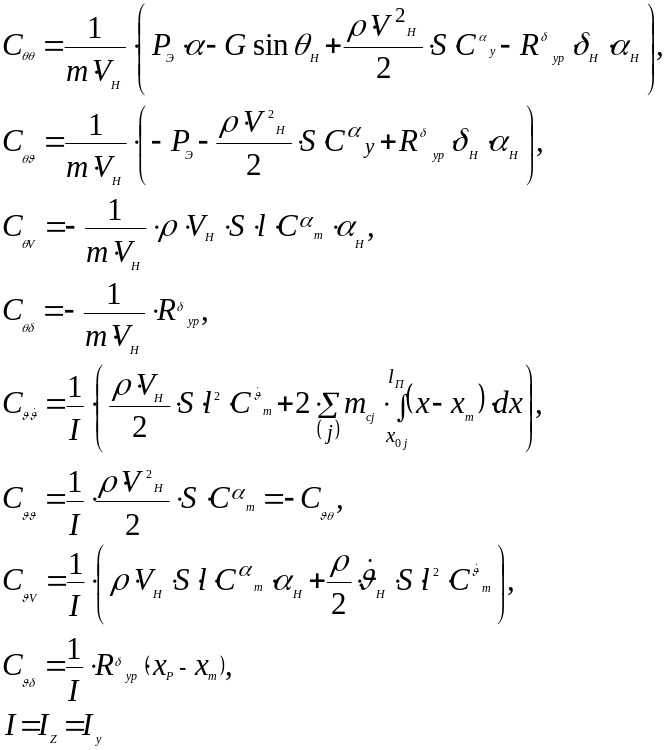(182)

В отличие от уравнений (171) уравнения (182) называются уравнениями возмущенного движения, или уравнениями в вариациях. Это линейные дифференциальные уравнения с переменными коэффициентами. Коэффициенты уравнений определяются через характеристики ракеты , параметры невозмущенного движения , , плотность воздуха и аэродинамические коэффициенты, т.е. могут быть вычислены.

Запишем уравнения возмущенного движения ракеты в скоростной системе координат в плоскости рыскания.

Невозмущенное движение ракеты происходит в плоскости тангажа, так в плоскости рыскания все параметры номинального движения и внешние силы тождественно равны нулю. Возмущения в плоскости рыскания считаем малыми и определяем их через угол рыскания ψ, угол скольжения β, угол поворота траектории по отношению к плоскости невозмущенного движения σ и угол поворота управляющих органов δ.

Ввиду малости возмущений и наличия плоскостей симметрии ракеты возмущенное движение в плоскости рыскания не будет зависеть от возмущений в плоскости тангажа.

С появлением угла скольжения β возникает поперечная аэродинамическая сила Ζ и аэродинамический момент М_уа, равные:

,

При этом вследствие осевой симметрии ракеты при α_Н=0 производная

,а .

При вращении ракеты с угловой скоростью возникает демпфирующий момент в плоскости рыскания. На основании уравнения (111) запишем выражение для полного демпфирующего момента как сумму аэродинамического демпфирующего момента и кориолисова демпфирующего момента.

Уравнения возмущенного движения в плоскости рыскания можно получить из уравнений (179), заменив в них вариации Θ, ν, α вариациями σ, ψ, β соответственно и приняв G = 0, β_Н = ψ_Н = δ_Н = 0. В этом случае второе и третье уравнения не будут связаны с первым уравнением.

Итак, уравнения возмущенного движения в скоростной системе координат будут иметь вид:

(183)

где

(184)

При принятых ранее допущениях малое возмущение γ в плоскости крена будет зависеть только от возмущений углов поворота управляющих органов. Момент управляющих сил рулей относительно продольной оси ракеты равен

где

δ_х – обобщенный угол поворота управляющего органа относительно продольной оси О_х1;

– градиент управляющего момента.

Уравнение возмущенного движения относительно продольной оси будет

(185)

Здесь через обозначен демпфирующий момент относительно продольной оси, который возникает, например, при наличии на корпусе ракеты оперения.

Для изучения кратковременных возмущений на небольшом интервале времени будем принимать траекторию невозмущенного движения центра масс ракеты прямолинейной. Составим уравнение возмущенного движения в плоскости тангажа в неподвижной системе координат О_ху. Такие уравнения удобны при изучении возмущенного движения ракеты с учетом колебаний жидкости в баках и упругих колебаний корпуса ракеты.

Ось ОХ неподвижной системы координат направим по касательной к траектории невозмущенного движения, ось ОУ – перпендикулярно ей (фиг.72).

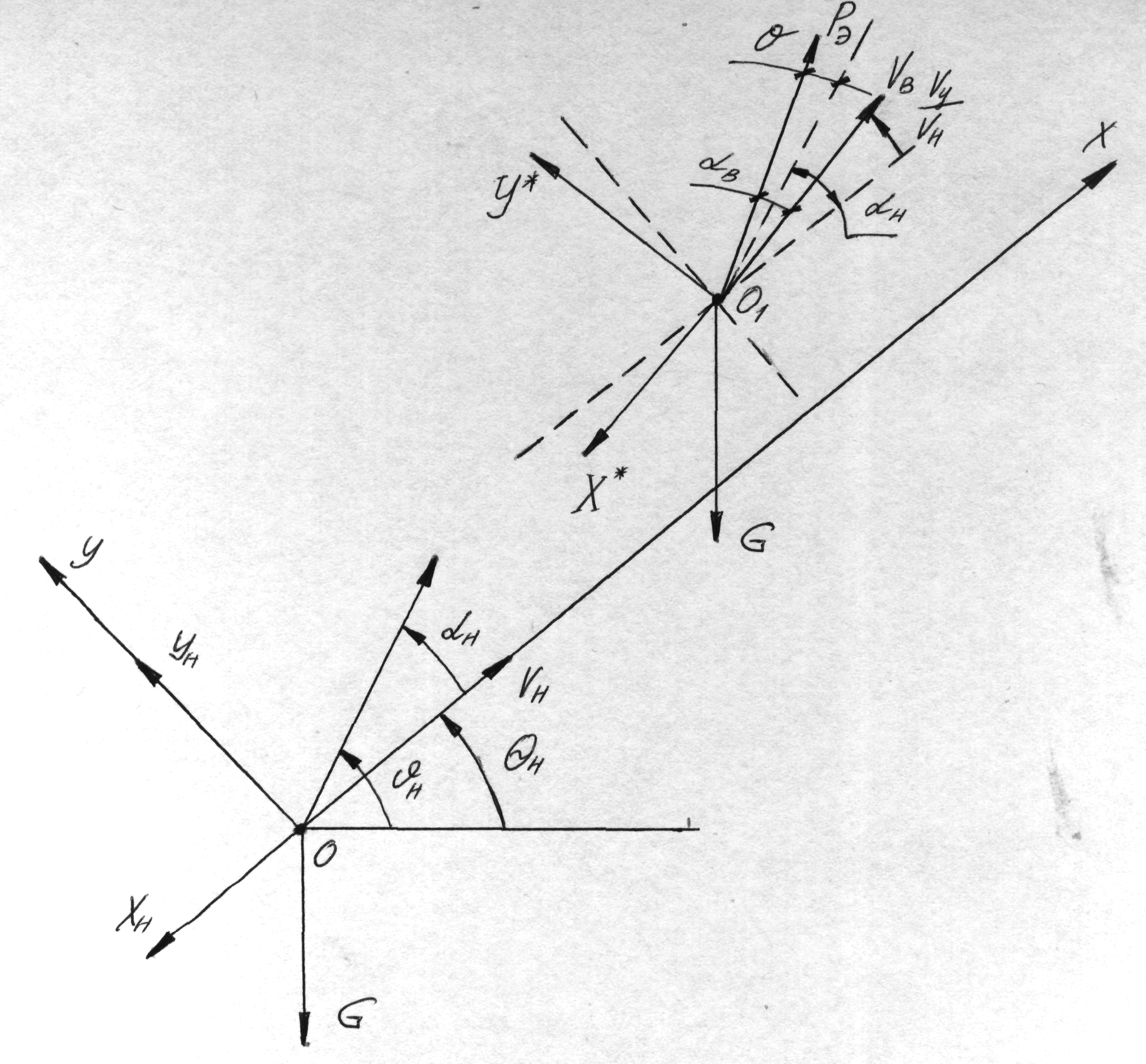
Фиг.72

Невозмущенное (номинальное) движение ракеты в плоскости тангажа описывается следующими уравнениями:

(186)

Обозначим малые возмущения проекций скорости центра масс на неподвижные оси координат через и , малое возмущение угла тангажа , а угол поворота управляющего органа через . В результате, возмущенный вектор скорости отклонится на угол , поэтому новое значение угла атаки будет

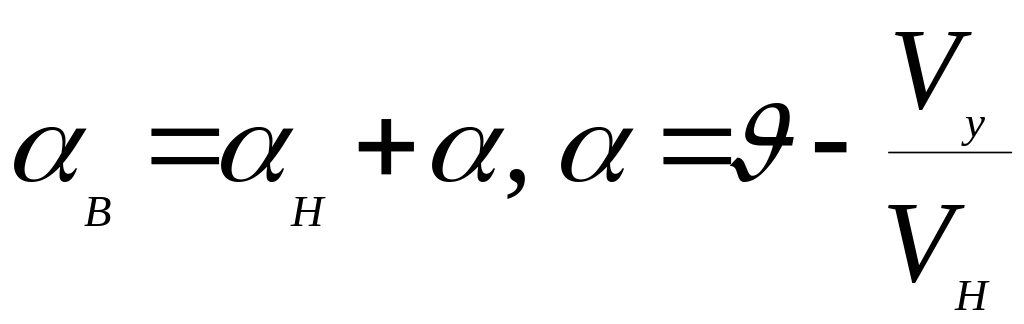(187)

Теперь плоское движение в неподвижной системе координат Oxy определяется следующими уравнениями:

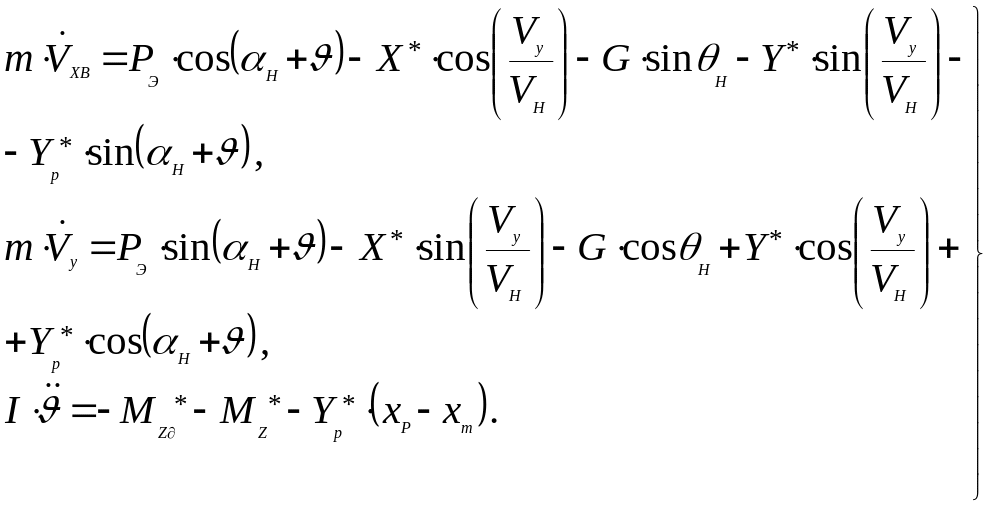(188)

Выразим возмущенные силы и моменты , , , , через величины (178) и произведя вычитание (186) из (188), получим уравнения движения ракеты в неподвижной системе координат относительно возмущений , , и :

(189)

В первом уравнении коэффициенты равны:

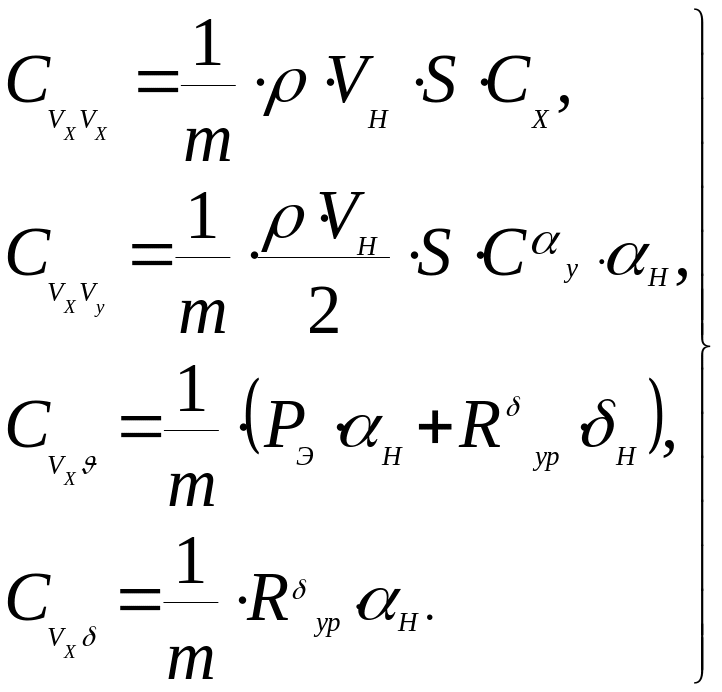(190)

В первом уравнении вариация принята равной вариации .

Во втором и третьем уравнениях коэффициенты равны:

(191)

Остальные коэффициенты вычисляются по формулам (182).

Анализ уравнений возмущенного движения.

Коэффициенты уравнений возмущенного движения (180), (183), (185), (189) осуществляются через характеристики ракеты, плотность воздуха и кинематические параметры невозмущенного движения, т.е. являются известными функциями времени. Несмотря на то, что перечисленные системы уравнений линейны относительно возмущений, их анализ затруднен наличием переменных коэффициентов. Такие уравнения обычно решаются методами численного интегрирования.

Для предварительного анализа при проектировании ракеты и системы управления применяется прием «замораживания» коэффициентов, при помощи которого можно получить хоть и грубые, но более общие (обозримые, наглядные) результаты.

Сущность приема «замораживания» коэффициентов заключается в следующем. Пусть, например, коэффициенты уравнений возмущенного движения (180) определены для некоторой траектории невозмущенного движения. На этой траектории выбирают несколько характерных точек и вместо системы уравнений (180) с переменными коэффициентами рассматривают совокупность аналогичных систем с постоянными коэффициентами , представляющие собой значения коэффициентов уравнений (180) в фиксированные моменты времени t_К. Т.е. время полета разбивают на небольшие промежутки, включающие точки t_К и в этих промежутках коэффициенты уравнений считают постоянными.

Прием «замораживания» коэффициентов позволяет применить хорошо известные методы решения линейных дифференциальных уравнений с постоянными коэффициентами, методы оценки устойчивости решений, частотные методы автоматического регулирования. Однако полученные результаты следует рассматривать как предварительные, носящие в основном качественный характер.

Рассмотрим возмущенное движение ракеты в плоскости тангажа, система (180). Для упрощения примем, что невозмущенное движение представляет прямолинейный установившийся полет и что коэффициенты уравнений постоянны. Используем символическую запись , …..

Характеристический полином для системы уравнений (180) при будет

(192)

Коэффициенты а₁, а₂, а₃, а₄ – вещественные, итак корни полинома могут быть или вещественными или комплексно сопряженными. Как показывает практика для статически устойчивой ракеты, характеристический полином имеет 2 пары комплексно сопряженных корней, причем вещественная и мнимая части одной пары корней по абсолютной величине во много раз превышают вещественные и мнимые части другой пары корней. Это значит, что свободное возмущенное движение можно представить в виде суммы двух движений – короткопериодического, соответствующего паре больших по модулю комплексных корней, и длиннопериодического соответствующего паре малых по модулю комплексных корней.

Например, для гипотетической статически устойчивой ракеты в некоторый момент времени корни полинома (192) имеют следующие значения

;

Периоды колебаний соответственно равны

;

Пусть возмущенное движение ракеты вызвано мгновенным отклонением рулей, причем в момент отклонения рулей . Если условно принять, что корни характеристического уравнения равны , то для вариаций получим выражение вида

,

Где , причем для вариации всегда . Следовательно, изменение определяется главным образом медленнозатухающим слагаемым и является длиннопериодическим.

Изменение угла атаки определяется в основном быстрозатухающими слагаемыми и относится к короткопериодическому движению. В выражениях для углов и как медленно затухающие, так и быстро затухающие слагаемые имеют существенное значение.

Такой характер изменения параметров возмущенного движения во времени не зависит от типа ракеты. Ракета может очень быстро изменять угол атаки, вращаясь относительно центра масс. В то же время скорость полета ракеты изменяется по величине сравнительно медленно, т.к. очень малы продольные ускорения , обусловленные изменением сил вследствие изменения угла атаки.

Это обстоятельство позволяет сделать следующий вывод – если и суть вариации первого порядка, то вариация ускорения , вызванная отклонением и , будет величиной второго порядка малости. Другими словами, в линейной постановке продольное ускорение ракеты не зависит от малых отклонений и .

Таким образом, возмущенное движение ракеты можно считать состоящим из двух этапов.

Первый этап – короткопериодический, состоящий в основном из вращения ракеты относительно центра масс и быстрого изменения угла атаки. В конце этого этапа момент аэродинамических сил относительно поперечной оси будет практически уравновешен моментом управляющих сил, а угловая скорость близка к нулю. Однако при наличии отклонений и условия равновесия сил в направлении нормали и касательной к траектории выполнятся, не будут.

Второй этап движения – длиннопериодический, медленнозатухающий. Этот этап продолжается до тех пор, не будет достигнуто равновесие сил. Это этап медленного изменения скорости V.

Управление полетом в основном заключается в изменении направления вектора силы тяги двигательной установки - . Эта сила направлена по продольной оси ракеты и, следовательно, направление ее определяется углом тангажа . Т.к. угол атаки и угол тангажа изменяются практически только на короткопериодичном этапе возмущенного движения, то именно этот этап и является важным при проектировании системы стабилизации углового движения. Вместе с тем при анализе систем регулирования скорости основным этапом будет длиннопериодический.

В малом влиянии скорости на вариации и нетрудно убедиться, если сравнить значения коэффициентов связей второго и третьего уравнений (180). Так, во втором уравнении:

,

А в третьем:

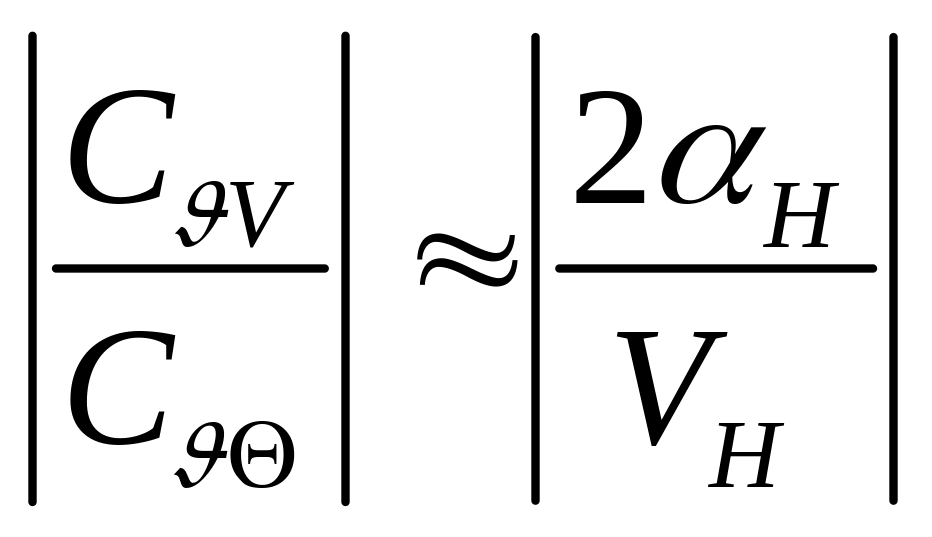
Только в начале полета, когда скорость мала, а значителен, связь уравнений может быть существенной.

Таким образом, для краткопериодического этапа возмущенного движения в уравнениях (180) принимают . Тогда

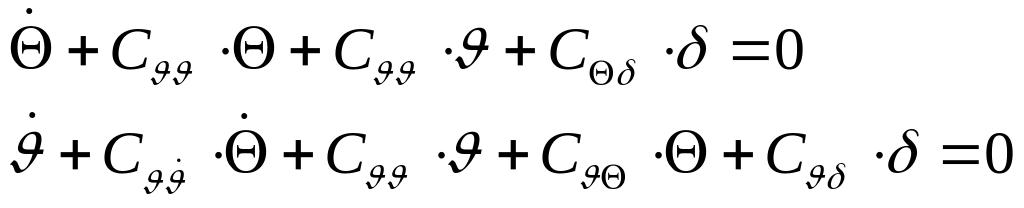(193)

Уравнения (193) называются уравнениями возмущенного движения в плоскости тангажа.

Из анализа формул (182) следует, что значения коэффициентов практически не меняются, если малые величины и положит равными нулю, т.е. считать, что невозмущенное движение происходит с . При таком предположении уравнения (193) будут отличаться от уравнений возмущенного движения в плоскости рыскания (183) всего лишь на величину одного коэффициента. Формула для содержит вариацию проекции сил веса на нормаль к траектории ( ), тогда как на движение рыскания силы веса влияния не оказывают, поэтому коэффициент от них не зависит.

В связанной и неподвижной системах координат проекция сил на продольную ось при возмущениях изменяется незначительно. Поэтому, как и в случае скоростной системы координат, в силу малости ускорения на первом этапе возмущенного движения вариация оказывается малой по сравнению с вариациями и . На этом основании во втором и третьем уравнениях (189) на этапе короткопериодического возмущенного движения можно положить и рассматривать эти уравнения (2) и (3) не зависимо от первого.

Таким образом, кроме уравнений (193) уравнения короткопериодического возмущенного движения в плоскости тангажа можно записать:

а) в связанной системе координат:

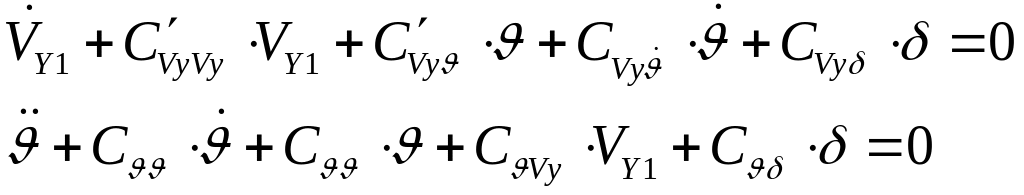(194)

б) в неподвижной системе координат:

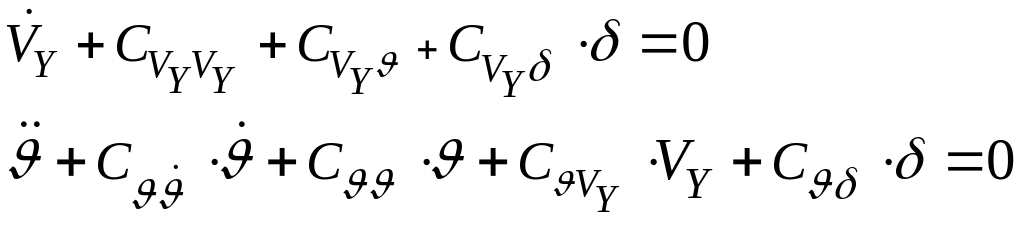(195)

Уравнения короткопериодического возмущенного движения в плоскости рыскания в скоростной системе координат на основании (183) примут вид:

(196)

Покажем, что уравнения (195) тождественны уравнениям (193). В самом деле, т.к. на начальном этапе возмущенного движения , то из первого уравнения (186) имеем равенство сил:

(197)

Кроме того, в неподвижной системе координат имеем кинематическое

соотношение:

(198)

Сравнивая коэффициент из (182) с коэффициентом из (191) получим .

Принимая во внимание (184), получим также:

.

Будем полагать, что уравнение системы управления (173) допускает линеаризацию. Проведя ее, получим уравнение системы управления относительно вариаций:

(199)

Уравнения (193) – (195) совместно с (199) образуют однородную линейную систему дифференциальных уравнений, описывающих возмущенное движение замкнутой системы автоматического регулирования.