12.2. Участки траектории полета баллистической ракеты и рн.

12.2.1 Участок выведения. Номинальные параметры и возмущенное движение

Уже несколько раз говорили, что расчетными режимами полета и фактически реализуемыми есть определенные различия. Займемся этим вопросом специально. Начнем с того, что еще раз выпишем 3 уравнения движения и определимся с углами, силами и моментами, характеризующими полет ракеты.

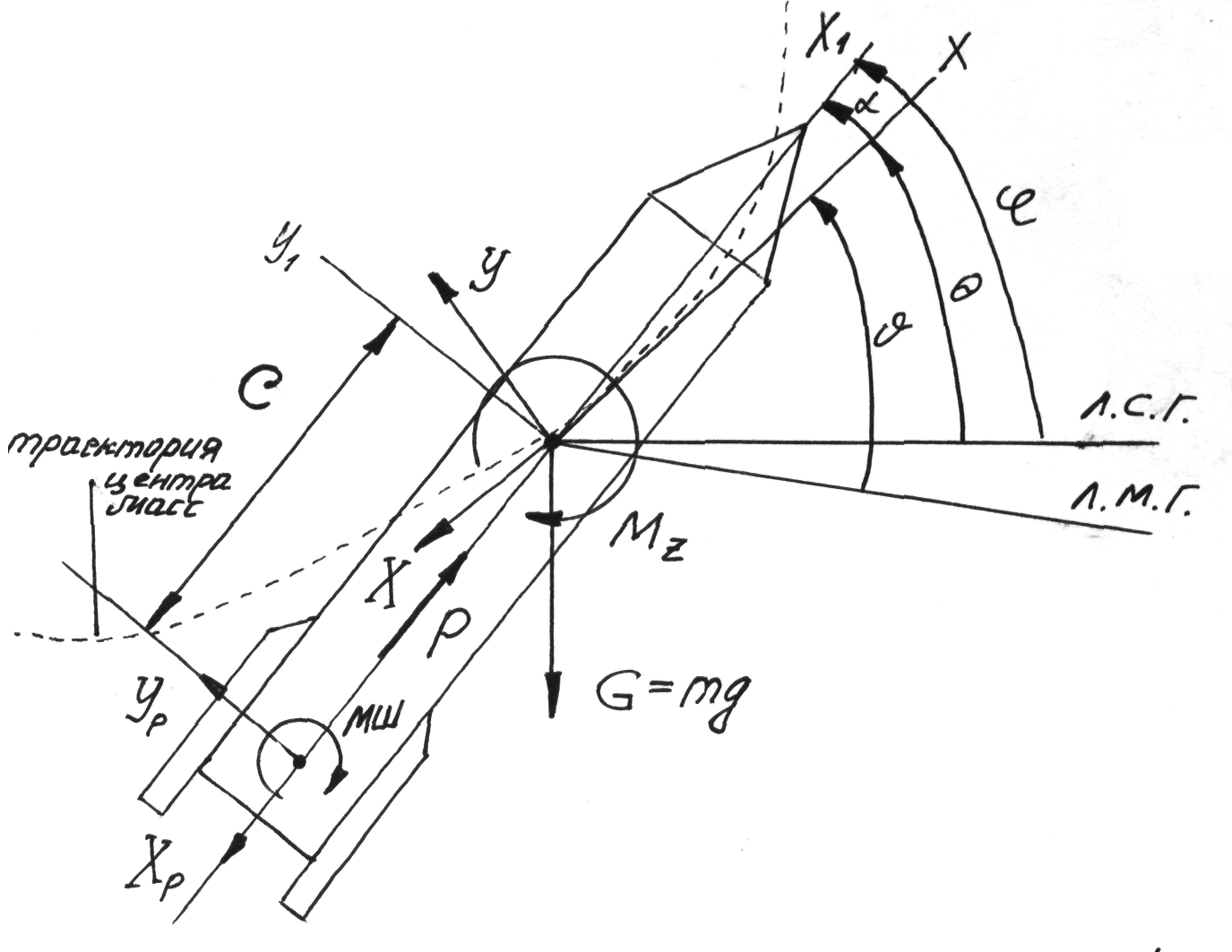
Фиг.63

Согласно закону Ньютона произведение массы ракеты на тангенциальное ускорение равно сумме проекций сил на касательную к траектории. Следовательно:

(141)

Специфические особенности движения ракеты, как тела переменной массы, учтены в выражении тяги Р.

Нормальное ускорение, обусловленное искривлением траектории, равно , где - радиус кривизны траектории. На фигуре 63 траектория показана с положительной кривизной, в действительности ее кривизна отрицательная.

Выражение кривизны может быть написано в виде:

,

где:

– угол наклона касательной к траектории, отсчитываемый от неподвижного стартового горизонта (фиг.63);

– элемент дуги траектории.

Следовательно, нормальное ускорение, направленное к центру кривизны равно .

Спроектировав все силы на нормаль к траектории полета, получим:

(143)

Отбросим в уравнении (143) шарнирный момент как величину малую, а аэродинамический момент заменим суммой статического и демпфирующего:

(144)

(145)

. (146)

И добавим недостающие геометрические соотношения, характеризующие траекторию полета.

Фиг. 64

Из фигуры 64а) следуют кинематические соотношения:

(147)

Аналогично в полярной системе координат (фиг. 64б):

(148)

Из выражений (147), (148) после интегрирования определятся ортодромная дальность и местная высота где радиус Земли.

Согласно фигуре 61 для углов могут быть написаны следующие очевидные соотношения:

(149)

Рассмотрим некоторый отрезок времени, в течение которого происходит программный разворот ракеты, когда угол тангажа плавно уменьшается, а угол отклонения рулей возрастает (фиг.65 а).

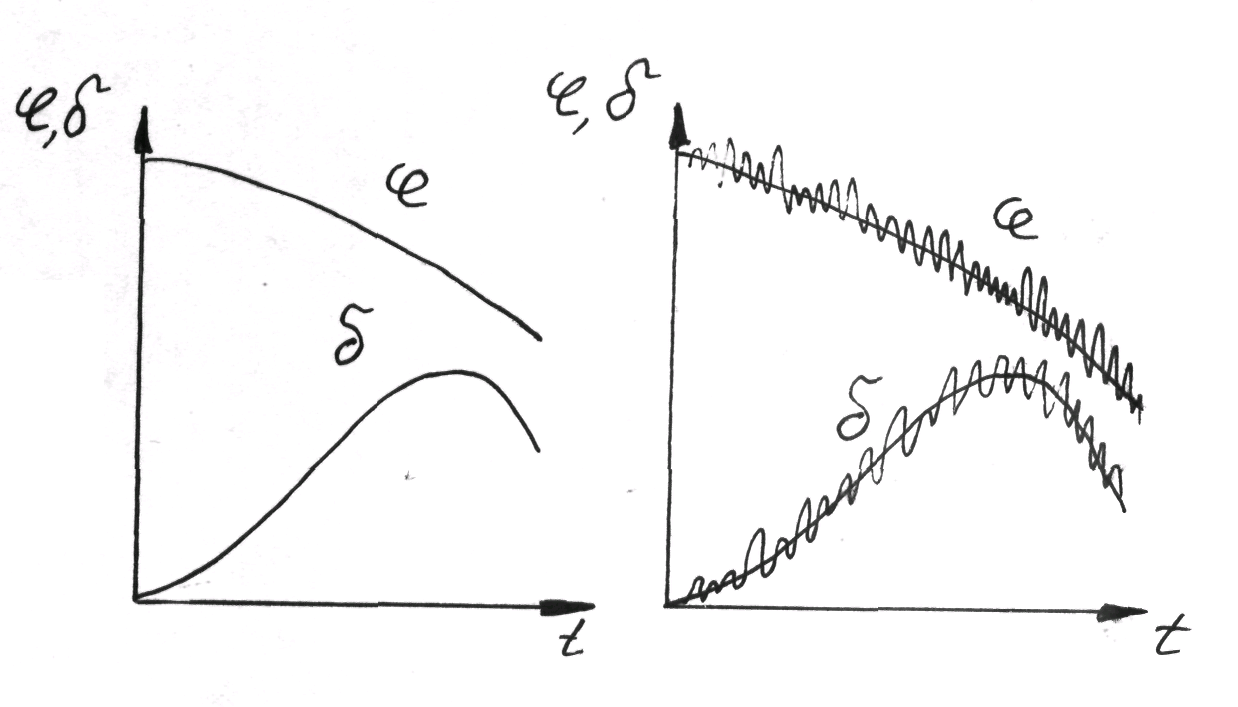
Фиг.65 Функции номинального и возмущенного движений.

Плавные кривые (фиг.65 а) – только теоретические, на бумаге. В действительности, ракета испытывает постоянные возмущения (фиг.65 б). В среднем, законы уменьшения и роста сохраняются, но на гладкие зависимости накладываются непредусмотренные отклонения с переменной амплитудой. Если эти отклонения подвергнуть анализу, разложив на гармоники, то можно, прежде всего, обнаружить некоторые характерные, явно выраженные частоты, основные из которых, - самые низкие,- поддаются логическому толкованию, а в ряде случаев можно найти причины той или иной частоты.

В частности, для оперённой статически устойчивой ракеты первой появляется собственная частота колебаний жесткого корпуса в аэродинамическом потоке. Роль восстанавливающего момента играет аэродинамический статический момент, а частота зависит как от запаса устойчивости, так и от момента инерции, возрастающей относительно поперечной оси.

Ракета колеблется подобно флюгеру относительно среднего положения, заданного ей управляющими органами.

Для длинной ракеты с тонкими несущими баками в спектре частот становится заметной частота поперечных изгибных колебаний корпуса как упругой балки.

При анализе можно обнаружить и другие характерные частоты, которые меняются во времени по мере изменения массы ракеты и траекторных параметров. В некоторых случаях амплитуда отдельных форм колебаний может принять недопустимо большие значения. Принимаются меры к их устранению.

Термин «возмущение» – это необязательно атмосферные явления. Здесь присутствуют многие факторы: и атмосферные воздействия, и работа автомата стабилизации, и смена режимов полета.

Обращаясь к уравнениям (144) – (149), легко понять, что изменения колебательного характера свойственны и другим величинам – углам, моментам, силам. Будут различные амплитуды, сдвиги по фазе, но общая картина останется неизменной.

Изменениям колебательного характера подвержены углы что непосредственно вытекает из геометрических соотношений (147). Этим свойством обладают и моменты: статический, демпфирующий и кориолисов.

Подъемная сила и управляющая пропорциональны углам и . Следовательно, и они приобретают колебательную составляющую. На тягу Р угловые возмущения не влияют.

Лобовое сопротивление при малых изменениях также практически не меняется, как и потери на органах управления .

Если обратиться к массе m жидкостной ракеты, то тут есть одна особенность.

В частично заполненных баках сама жидкость приходит в колебательное движение, сдвинутое по фазе к угловым колебаниям корпуса, и поведение системы заметно меняется, т.к. масса жидкого топлива составляет основную часть общей массы ракеты. Хорошо ещё, что в этом относительном движении участвует не вся масса жидкости, а только та её часть, которая расположена ближе к свободной поверхности. Мы предполагаем, что жидкость неподвижна или сильно задемпфирована перегородками. Для твердотопливных ракет подобной проблемы не возникает.

Итак, движение, для описания которого предназначены уравнения (144)- (149), являются возмущенными, и практически все входящие в уравнения слагаемые могут быть представлены в виде:

,

где – возмущенное значение некоторой переменной, любой;

– ее номинальное значение;

– само возмущение, которое допустимо рассматривать как малое.

Слагаемые и существенно различаются и в своих производных.

Например, угол тангажа φ_н меняется относительно медленно, следовательно, мало. Функция Δφ меняется весьма быстро и ее производные и существенно больше, чем и .

То же самое можно сказать и о всех прочих величинах, подверженных быстропротекающим изменениям. Правда, среди возмущений некоторых величин, например, φ, m, P, есть и медленно изменяющиеся отклонения от номинала, которые можно учесть заранее и замерить в полете. То, что предсказуемо, учитывается в уточненных баллистических расчетах. То, что предсказать нельзя, становится объектом регулирования.