11.1.7. Уравнения системы наведения.

Для выяснения принципа формирования управляющего сигнала обратимся к основным положениям теории автоматического регулирования.

Принцип работы системы управления летательным аппаратом, как и любой системы автоматического регулирования, заключается в следующем. Всякая ошибка системы , т.е. разность между требуемым и действительным значением регулируемого параметра:

(138)

независимо от причины её возникновения, порождает ответную реакцию системы управления, направленную на уничтожение возникающей ошибки. Следовательно, система управления работает только тогда, когда имеется ошибка ε. По этой причине, а также в результате воздействия возмущений в реальных условиях, ошибка ε всегда отлична от нуля, хотя система управления все время стремится её уничтожить. Чем меньше ошибка, тем точнее работает система управления. В идеальном случае в течение всего процесса управления фактическое значение регулирующего параметра равнялось бы его требуемому значению:

(139)

Уравнение (138) назовем уравнением связи, накладываемым методом полета на движение летательного аппарата, а соответствующее ему уравнение (139) – уравнением идеальной связи.

Уравнение идеальной связи определяет теоретическую траекторию ЛА. Действительная траектория всегда отличается от теоретической в силу различных причин. В основу формирования управляющего сигнала закладывается ошибка , характеризующая отклонение действительной траектории от теоретической.

Уравнения системы наведения связывают выходные величины – управляющие сигналы - с выходными величинами – ошибками :

(140)

Если в уравнения связей (138) и уравнения системы наведения (140), кроме 21 параметра:

,

а также известных параметров движения цели и некоторых известных функций времени , не будут входить какие-либо другие переменные, то система уравнений (123), (135) и (137) с учетом (138) и (140) замкнется. Тогда траектория летательного аппарата (при отсутствии возмущений) будет определяться начальными условиями и уравнениями связей.

12. Траектории движения летательного аппарата.

12.1. Траектории полета баллистических ракет(бр) и ракет-носителей(рн).

Тяжелые баллистические ракеты и ракетоносители всегда стартуют вертикально. Такой старт является единственно возможным. Тонкостенная конструкция ракеты не способна выдержать боковые нагрузки при движении и сходе с направляющих, а пусковая установка при наклонном старте баллистической ракеты и ракетоносителя по своему весу и габаритам будет равна египетским пирамидам.

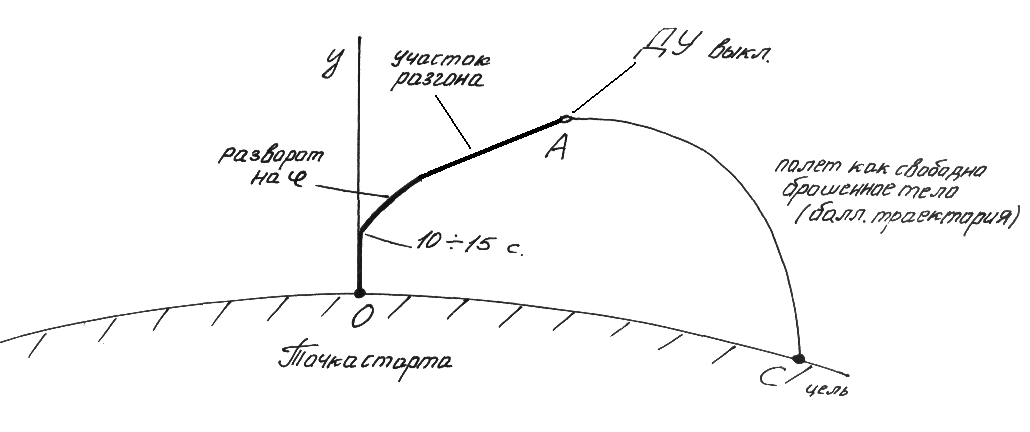
Траекторию баллистической ракеты можно в первом приближении рассматривать как плоскую кривую. Участок от старта до точки А называется активным участком или участком выведения. Та часть траектории, где ракета испытывает заметное воздействие аэродинамических сил, называется атмосферным участком полета. Для тяжелых баллистических ракет атмосферный участок полета всегда меньше активного. То же самое можно сказать и о составных ракетоносителей. Отделение блоков первой ступени производится в условиях, когда аэродинамические силы малы.

После выключения двигательной установки(ДУ) в точке А ракета летит как свободно брошенное тело и вид траектории определяется только притяжением Земли и начальными условиями – координатами точки и вектором скорости в момент выключения ДУ. При подходе к цели ракета входит в плотные слои атмосферы, испытывает торможение и значительный нагрев. Этот участок траектории называется участком входа в атмосферу.

Траектория выведения ракетоносителя, например, двухступенчатой, по своему характеру практически не отличается от траектории дальней баллистической ракеты

.

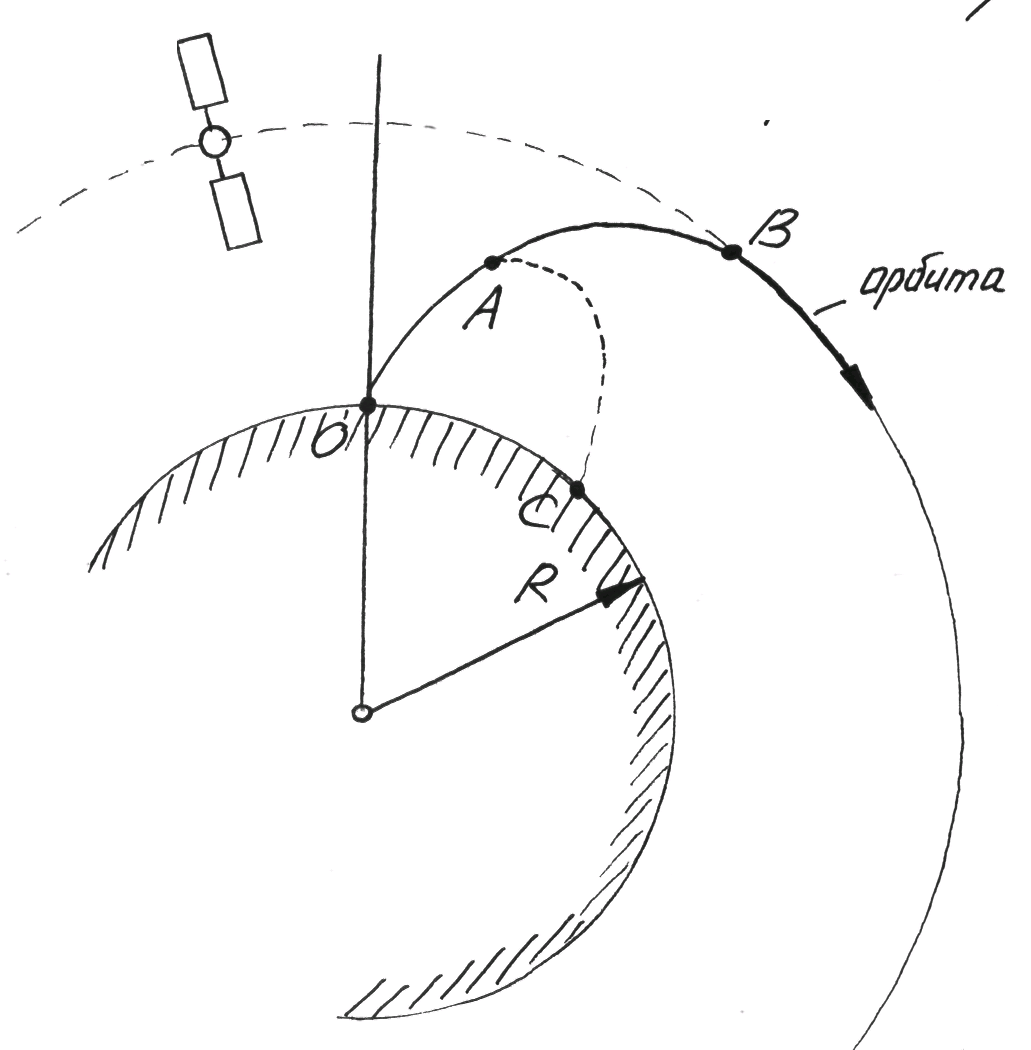
В точке А заканчивает работу ДУ первой ступени. Блоки первой ступени отстреливаются и падают на Землю в точке С. Вторая ступень сообщает ракете необходимую скорость и в конце активного участка в точке В уже на орбите, ДУ отключаются.

Разворот ракеты на участке выведения осуществляется органами управления по заранее выбранной программе с помощью СУ.

Выведение ракеты характеризуется программным углом тангажа - углом между осью ракеты и стартовым горизонтом (фиг. 61).

Фиг. 61

Зависимость угла от времени называется программой изменения угла тангажа . В простейших случаях для БР относительно большой дальности график программы угла тангажа имеет вид кривой на фиг. 62.

Фиг.62

Программный угол тангажа близок к углу наклона траектории , но не равен ему из-за угла атаки .

Выбор способа выведения баллистической ракеты (БР) относится к классу краевых задач, когда необходимо выбрать начальные параметры программного движения при заданных условиях в конце траектории. Для боевых ракет задаются наземные координаты цели. Для РН задается высота и вектор скорости в конце участка выведения. Для космических траекторий в краевые условия входит также астрономическое время, отвечающее моменту выведения объекта.

Траектория БР с необходимой точностью определяется методами численного интегрирования дифференциальных уравнений движения. Но это возможно лишь при условии, когда известны основные параметры ракеты – ее весовые и тяговые характеристики, а найти их значения можно, только располагая необходимыми сведениями о траектории. Возникает замкнутый круг неопределенностей, характерный для начальной стадии проектирования ракеты.