Фиг.47 Переход от начальной стартовой системы координат к связанной.

Пусть начала обеих систем совпадают.

Через центр масс летательного аппарата – начало связанной системы координат, проведём оси Ox₀y₀z₀, параллельные осям начальной стартовой системы координат.

Ориентация летательного аппарата относительно начальной стартовой системы координат определяется 3-мя углами между связанной Ox₁y₁z₁ и начальной стартовой системой координат Ox₀y₀z₀, а именно:

- углом тангажа φ – углом между продольной осью летательного аппарата Ox₁ и плоскостью Ox₀z₀. Угол тангажа определяет наклон аппарата к горизонту;

- углом рыскания ψ – между проекцией продольной оси летательного аппарата Ox₁ на плоскость Ox₀z₀ и осью Ox₀. Угол рыскания – отклонение направления полёта летательного аппарата от первоначального, ракеты – от плоскости стрельбы.

- углом крена γ – между поперечной осью летательного аппарата Oy₁ и плоскостью, проходящей через оси Ox₁ и Oy₀.

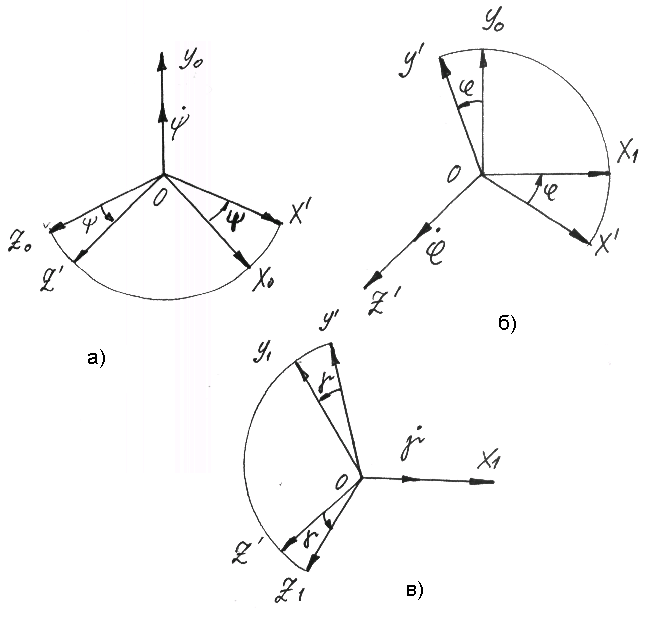
Фиг.48 Последовательные повороты на углы:

а) поворот на угол рыскания ψ;

б) поворот на угол тангажа φ;

в) поворот на угол крена γ.

Первый поворот осуществляется на угол ψ вокруг инерциальной оси Oy₀ (фиг.48,а).

Второй поворот происходит вокруг промежуточной оси Oz’ на угол φ (фиг.48,б).

Третий поворот выполняется вокруг связанной оси Ox₁ на угол γ (фиг.48,в).

Таким образом, в результате последовательных поворотов ан углы ψ, φ, γ, происходит переход от начальной стартовой Ox₀y₀z₀ к связанной Ox₁y₁z₁ системе координат. Именно эти углы обычно измеряют с помощью датчиков системы управления (СУ).

Зная углы ψ, φ, γ, в соответствии с правилами аналитической геометрии можно пересчитать составляющие силы и моменты в одной системе координат на составляющие в другой.

Направляющие косинусы углов между осями связанной и начальной стартовой систем координат приведены в таблице 1.

Табл.1

Связанная система коорд.	Начальная стартовая система координат
	Оси	Ox0	Oy0	Oz0
	Ox1	φ=cos φ	sinφ	-cosφ = -ψcosφ
	Oy1	φ + + =- -sin φ	cosφ = cosφ	γ+ + sinφ
	Oz1	φ + +	-cosφ	γ- - sinφ

Одна из задач системы управления полётом ракеты состоит в том, чтобы не допустить возникновения больших значений углов ψ (рыскания) и γ (крена), а угол φ (тангажа) изменять по определённому, заранее заданному закону.

Поскольку мы рассматриваем полёт ракеты с исправно работающей системой управления, будем считать, что углы ψ и γ малы и заменять их косинусы единицей, а синусы – углами => , , .

Производя такую замену и отбрасывая члены, содержащие произведения малых величин, получают упрощённые формулы, которыми будем пользоваться в дальнейшем.

10.3.2. Направляющие косинусы между осями земной и связанной систем координат.

Начало связанной системы координат поместим в центр массы ракеты, ось Ox₁ направим по продольной оси ракеты к её головной части.

На старте ракета устанавливается вертикально, поэтому в момент пуска ось Ox₁ совпадает с осью Oy_з земной системы координат. Ось Oz₁ направлена так, чтобы она была параллельна оси Oz_з, тогда ось Oy₁ примет направление, противоположное направлению оси Ox_з. Иначе говоря, оси связанной системы координат в момент пуска совпадают с соответствующими осями земной системы координат, если земную систему координат повернуть на угол 90⁰ вокруг оси Oz_з в направлении от оси Ox_з к оси Oy_з (фиг.49):