9.2. Полное и частичное динамическое подобие. Критерии динамического подобия.

9.2.1. Полное динамическое подобие.

Закон динамического подобия Ньютона в коэффициентах подобия можно истолковать следующим образом.

Фиг.39.

Частицы жидкости участвуют в движении под действием внешних массовых и поверхностных сил (сил тяжести, давления и трения), результирующая которых равна силе инерции. Масштаб сил инерции определяется законом динамического подобия Ньютона. Следовательно, масштабы всех иных сил, действующих на сходственные жидкие частицы и определяющих их движение, должен быть таким же.

Запишем закон динамического подобия Ньютона, выражая масштабы через физические величины:

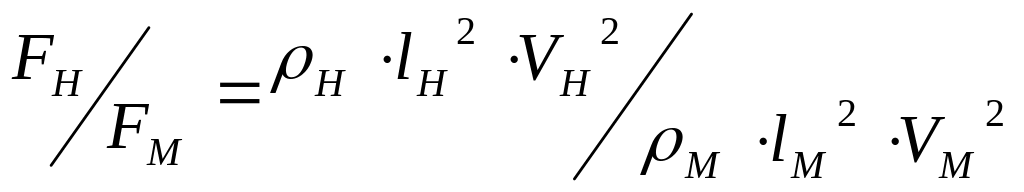
Перенесем члены с одинаковыми индексами по разные стороны равенства

. (65).

Это равенство является условием полного динамического подобия. Число Ne – критерий Ньютона полного динамического подобия.

Вообще критерием подобия называется безразмерные величины (числа), составленные из размерных физических параметров, определяющих рассматриваемое физическое явление.

На фиг.39 показаны многоугольники сил, действующих на натурную и модельную частицы в сходственных точках.

Учтены силы тяжести G, давления P, трения F_тр и их результирующая сила инерции J. При полном динамическом подобии они должны находиться в соотношении:

(66).

Потоки геометрически, кинематически и динамически подобные называются механически подобными.

9.2.2. Частичное динамическое подобие.

Перечисленные силы имеют различную физическую природу. Это обстоятельство затрудняет обеспечение полного динамического подобия натурного и модельного потоков.

Но существует довольно значительный класс течений, которые вызываются действием на жидкость какой-либо одной (преобладающей) силы. Для таких случаев можно получить критерий частичного динамического подобия, при котором учитывается действие преобладающей силы и силы инерции, а действием остальных сил пренебрегают.

Фиг.40.

Пусть преобладающей является сила тяжести G (фиг.40, а). Считаем, что в этом случае силами давления P и трения F_тр можно пренебречь. Тогда условие частичного динамического подобия сведется к равенству:

(67).

Но силы инерции согласно формулы (64) пропорциональны плотности, квадратам характерной длины и характерной скорости:

А силы тяжести – плотности и объему:

С учетом этих соотношений получим (68).

Полученный безразмерный параметр, пропорциональный отношению силы инерции к силам тяжести, называется числом Фруда.

Таким образом, для обеспечения частичного динамического подобия при преобладающем действием сил тяжести в сходственных точках числа Фруда должны быть одинаковыми, т.е.

или

Если преобладающей является сила трения F_тр (фиг.40,б), то можно пренебречь силами тяжести G и давления P.

Условие частичного динамического подобия сводится к равенству:

, отсюда .

Согласно закону вязкостного трения Ньютона, сила трения пропорциональна градиенту скорости и площади соприкасающихся слоев жидкости и равна:

.

Подставляя значения сил трения и инерции в условие частичного динамического подобия для рассматриваемого случая, получаем

.

Принимая

, отсюда (69).

– критерий Рейнольдса, учитывает отношения сил инерции и сил трения

,отсюда .

Когда преобладающим является действие сил давление P (фиг.40,в), поступая аналогично изложенному выше, приведем к условию:

.

Т.к. , получаем

или (69).

Eu – критерий Эйлера, учитывает действие сил давления и пропорциональность отношения сил инерции к силам давления.

В газообразной жидкости скорость звука , где ,

C_P - удельная теплоемкость в изобарическом процессе;

C_V – удельная теплоемкость в изохорическом процессе.

Для воздуха k ≈ 1,41.

Если движение газа моделируется движением того же газа, то k_M=k_H

При этом условии можно записать

В сходных точках число Маха M_H=M_M, учитывает сжимаемость жидкости. При М<1 – поток дозвуковой; М>1 – поток сверхзвуковой.

Если принять во внимание другие силы, то аналогичным путем можно найти иные критерии частичного динамического подобия.

Если преобладающей силой является сила поверхностного натяжения, получим критерий подобия Вебера:

Где σ – коэффициент поверхностного натяжения.

Если преобладает выталкивающая (Архимедова) сила – то получим число Ахимеда:

При установившихся течениях необходимо учитывать критерий подобия Струхаля:

Произведения различных критериев подобия представляют собой новые критерии подобия рассматриваемых физических явлений. Это объясняется пропорциональностью всех характеризующих физические явления параметров.