
- •«Сибирский государственный аэрокосмический университет им. Академика м.Ф. Решетнева»
- •1. Общие понятия.
- •1.1. Гипотеза непрерывности среды.
- •1.2. Основные физические свойства жидкости.
- •2. Предмет курса механики полёта беспилотных летательных аппаратов
- •2.1. Этапы исследования полёта летательных аппаратов.
- •2.2. Общие сведения об управлении полётом.
- •2.3. Силы, действующие на летательный аппарат.
- •Фиг.1 Силы, действующие на летательный аппарат в полёте
- •Силы, действующие на летательные аппараты при прямолинейном полёте.
- •Аэродинамическая нормальная сила.
- •Силы, действующие на летательный аппарат при горизонтальном манёвре без скольжения (вид сзади),
- •Аэродинамически осесимметричные схемы летательных аппаратов.
- •Нормальная сила, создаваемая двигателем.
- •Пример установки стартового двигателя под углом к оси летательного аппарата.
- •3. Основные соотношения теории реактивного движения.
- •3.1. Движение точки переменной массы. Тяга реактивного двигателя.
- •Тяга реактивного двигателя
- •Фиг.11 Силы, действующие на закреплённую ракету.
- •Фиг.12. Распределение сил давления по поверхности ракеты и по внутренней поверхности камеры реактивного двигателя.
- •Удельная тяга или удельный импульс
- •4. Органы управления летательными аппаратами.
- •Управление с помощью аэродинамических сил.
- •Фиг.14. Воздушные рули на задних кромках крыльев.
- •Фиг.15. Основные типы интерцепторов.
- •Фиг.16. Управляемый снаряд с поворотными крыльями
- •Фиг.17. Воздушные рули в схеме «утка»
- •Фиг.18. Пример схемы «бесхвостка»
- •Управление с помощью реактивных сил
- •Фиг.19. Схема управления летательным аппаратом посредством поворота ракетного двигателя.
- •Управление креном
- •Фиг.19. Силы, возникающие при отклонении элеронов
- •5. Система управления летательным аппаратом.
- •6. Уравнения движения жидкости и газа. Законы истечения.
- •6.1. Уравнение постоянства расхода (уравнение неразрывности).
- •6.2. Дифференциальные уравнения движения идеальной жидкости (уравнение Бернулли).
- •6.3. Геометрический и энергетический смысл уравнения Бернулли.
- •6.3.1. Геометрический смысл уравнения Бернулли.
- •6.3.2. Физический смысл уравнения Бернулли.
- •6.4. Уравнение Бернулли для потока реальной (вязкой) жидкости.
- •6.5. Применение уравнения Бернулли на практике.
- •Трубка полного напора (трубка Пито)
- •7. Аэродинамика и газодинамика. Характеристики потока.
- •7.1. Стандартная атмосфера (са)
- •7.2. Сжимаемость газов. Скорость распространения звука в газе.
- •Фиг. 20 Распространение слабых возмущений в неподвижной среде.
- •Фиг. 21 Распространение слабых возмущений в дозвуковом потоке.
- •Фиг. 22. Распространение слабых возмущений в сверхзвуковом потоке.
- •Фиг. 24. Огибающая семейства ударных волн в сверхзвуковом потоке. Приемник воздушного давления (пвд).
- •7.3 Теория ламинарного течения в круглых трубах.
- •7.3.1 Расход при ламинарном течении жидкости
- •7.3.2. Средняя скорость
- •7.3.3. Потери напора на трение
- •7.4. Турбулентный режим движения жидкости.
- •7.4.1. Особенности турбулентного течения. Пограничный слой.
- •8. Ламинарный и турбулентный пограничные слои.
- •8.1. Основные понятия пограничного слоя.
- •8.2. Выводы по разделу
- •8.3. Ламинарный и турбулентный режимы течения в пс.
- •Фиг. 27. Структура пс при переходе ламинарного течения в турбулентное.
- •8.3. Интегральное соотношение для установившегося течения в пограничном слое несжимаемой жидкости.
- •8.4. Пограничный слой и сопротивление трению плоской пластины в несжимаемой среде для ламинарного режима течения.
- •Фиг.31. Изменение напряжения трения и толщины пограничного слоя по длине пластины.
- •8.5. Отрыв течения в пограничном слое и образование вихрей. Аэродинамически удобообтекаемые и неудобообтекаемые тела.
- •Фиг.34. Развитие области отрывного течения за цилиндром.
- •Фиг.35. Развитие области отрывного течения за сферой.
- •Фиг.37. Зависимость коэффициента лобового сопротивления Сх от числа Rе для удобообтекаемого тела.
- •9. Элементы теории подобия потоков.
- •9.1. Геометрическое, кинематическое и динамическое подобие. Коэффициенты подобия.
- •9.2. Полное и частичное динамическое подобие. Критерии динамического подобия.
- •10. Динамика полёта.
- •10.1 Предмет и задачи курса динамики полёта.
- •10.2. Системы координат.
- •Фиг. 41 Геоцентрическая система координат
- •Фиг. 42 Геодезическая система координат
- •Фиг. 43 Земная система координат
- •Фиг. 44 Стартовая система координат
- •Фиг. 45 Ориентация связанных осей на старте летательного аппарата
- •Начальная стартовая система координат.
- •Фиг. 46 Местная географическая система координат
- •Геоцентрическая система координат.
- •Скоростная и полускоростная системы координат.
- •10.3. Косинусы углов между осями систем координат
- •10.3.1. Косинусы углов между осями связанной и начальной стартовой систем координат.
- •Фиг.47 Переход от начальной стартовой системы координат к связанной.
- •Фиг.48 Последовательные повороты на углы:
- •10.3.2. Направляющие косинусы между осями земной и связанной систем координат.
- •Фиг.49 Переход от земной системы координат к связанной системе координат.
- •10.3.3 Косинусы углов между осями полускоростной системы координат и местной географической системой координат.
- •Фиг.50 Переход от местной географической системы координат к полускоростной системе координат.
- •10.3.4. Косинусы углов между связанной и скоростной (поточной) системами координат.
- •Фиг.51 Связанная система осей координат.
- •Фиг.52 Скоростная система координат .
- •Фиг.53. Переход от скоростных осей к связанным осям.
- •11. Уравнения движения ла.
- •11.1. Принцип составления уравнений полёта реактивного ла.
- •11.1.1. Теорема о количестве движения.
- •11.1.2. Теорема о моменте количеств движения.
- •11.1.3. Принцип затвердевания.
- •11.1.4. Сила тяги реактивного двигателя (рд).
- •11.2. Уравнения движения ла в векторной форме
- •11.2.1. Уравнения движения центра масс.
- •11.2.2. Уравнение вращательного движения относительно центра масс.
- •11.2.3. Векторные уравнения движения ла относительно Земли.
- •11.3. Уравнения движения летательного аппарата в скалярной форме.
- •11.4. Общая система уравнений движения летательного аппарата.
- •Кинематические уравнения движения центра масс летательного аппарата.
- •11.1.5.Связи, накладываемые на движение летательного аппарата системой управления.
- •11.1.6. Уравнения системы стабилизации.
- •11.1.7. Уравнения системы наведения.
- •12. Траектории движения летательного аппарата.
- •12.1. Траектории полета баллистических ракет(бр) и ракет-носителей(рн).
- •12.2. Участки траектории полета баллистической ракеты и рн.
- •12.2.1 Участок выведения. Номинальные параметры и возмущенное движение
- •Фиг.65 Функции номинального и возмущенного движений.
- •Уравнение баллистики.
- •Фиг.66 Отсчёт координат от теоретической вершины ракеты.
- •Программа выведения.
- •12.2. Полёт летательного аппарата в центральном поле тяготения за пределами атмосферы.
- •Фиг.68 к выводу уравнений движения в полярной системе координат.
- •Траектория движения в общем виде
- •Фиг.69 Траектории свободного полета при различных скоростях выведения.
- •12.3. Атмосферный участок (входа в атмосферу).
- •12.4. Уравнения возмущенного движения.
- •12.6. Передаточные функции и их свойства.
- •12.7. Частотные характеристики и частотный критерий устойчивости.
- •12.8.Структура автомата стабилизации.
- •12.9 Эффективность органов управления.
8.2. Выводы по разделу
1). Преимущество
применения условных толщин ПС
![]() перед действительной толщиной ПС
перед действительной толщиной ПС
![]() состоит в том, что они меньше зависят
от исходных данных расчета, например,
от закона распределения скорости в ПС.
состоит в том, что они меньше зависят
от исходных данных расчета, например,
от закона распределения скорости в ПС.
Сопоставления
величин
![]() для простоты можно произвести для случая
линейного
распределения скоростей в ПС. При этом
будет иметь место следующее соотношение:
для простоты можно произвести для случая
линейного
распределения скоростей в ПС. При этом
будет иметь место следующее соотношение:
 и
и 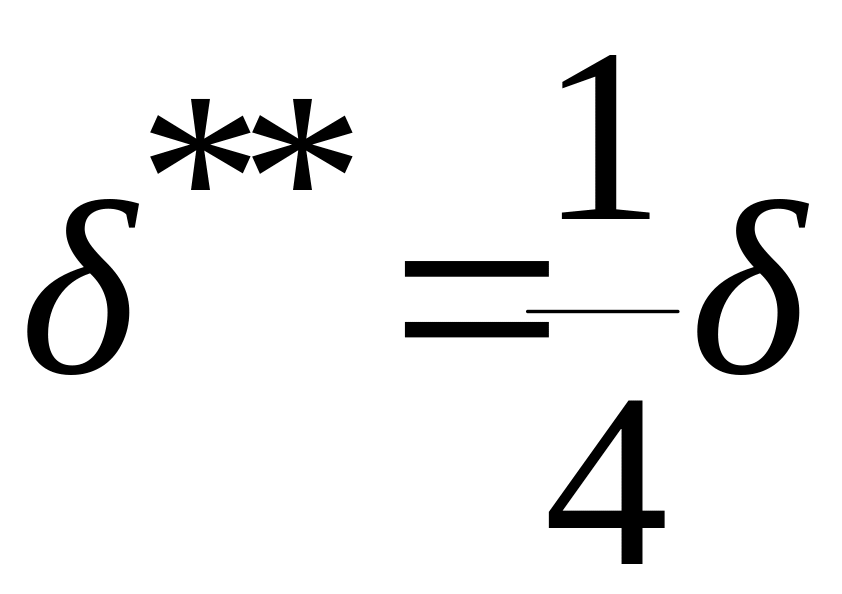 .
.
2). Большое
практическое значение имеет соотношение
,
справедливое для ПС. Оно означает, что
статическое давление
![]() не изменяется по высоте ПС. Это позволяет,
измерив давление на стенке, перенести
данные по распределению давления на
границу внешнего потока.
не изменяется по высоте ПС. Это позволяет,
измерив давление на стенке, перенести
данные по распределению давления на
границу внешнего потока.
8.3. Ламинарный и турбулентный режимы течения в пс.
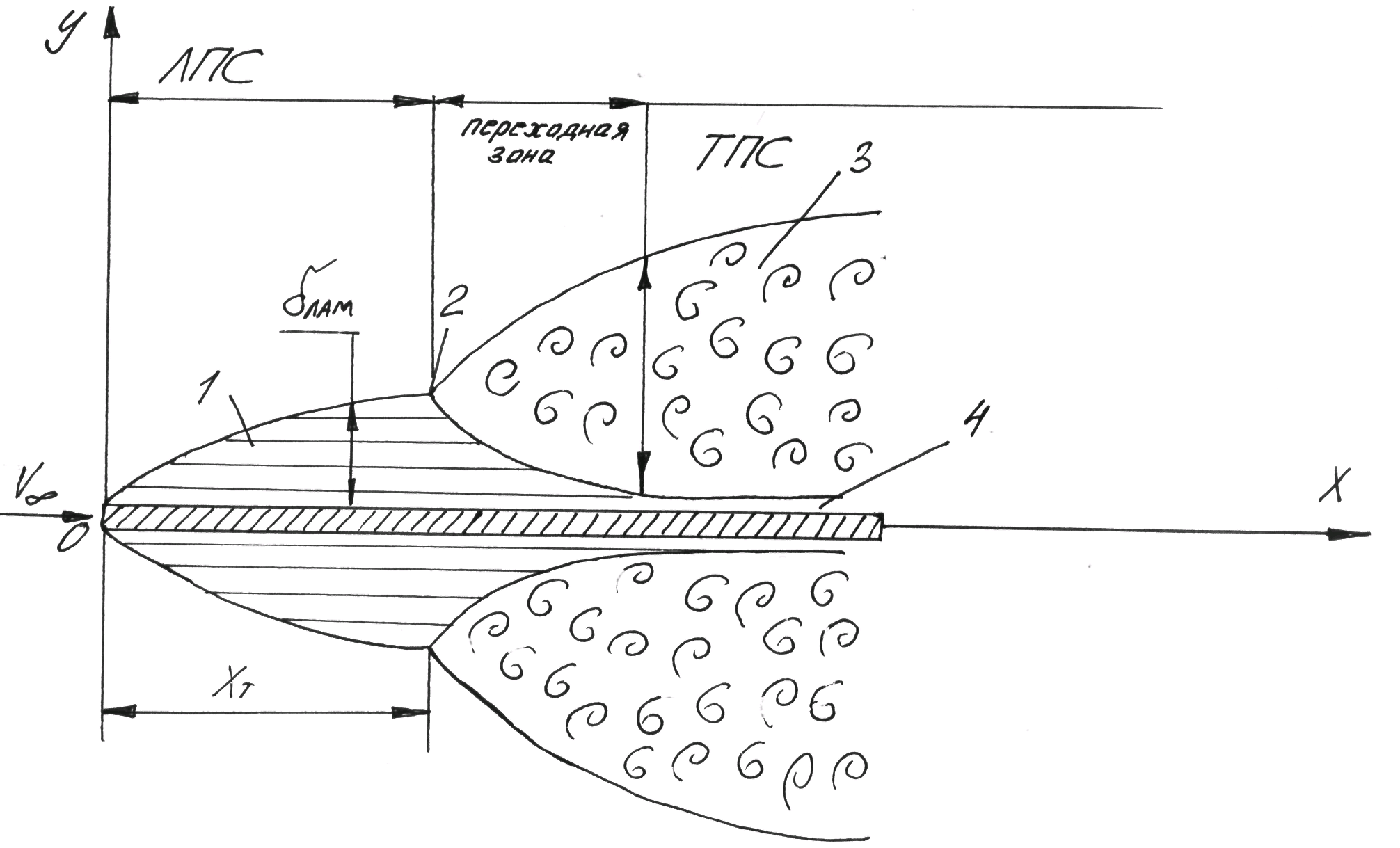
Фиг. 27. Структура пс при переходе ламинарного течения в турбулентное.
Если обтекаемая
пластина достаточно длинна, то структура
течения в ПС на разных расстояниях от
передней кромки пластины различна
(фиг.27). Вблизи передней кромки пластины
течение в пределах ПС слоистое, т.е. ПС
ламинарный (зона 1) (ЛПС). На некотором
удалении от передней кромки пластины
(![]() )
происходит потеря устойчивости
ламинарного течения и течение в ПС
переходит в турбулентное (ТПС). При
переходе ламинарного течения в
турбулентное сначала, в связи с потерей
устойчивости, линии тока становятся
волнистыми (точка перехода 2, переходная
зона-2), затем развивается устойчивое
турбулентное течение (зона 3).
)
происходит потеря устойчивости
ламинарного течения и течение в ПС
переходит в турбулентное (ТПС). При
переходе ламинарного течения в
турбулентное сначала, в связи с потерей
устойчивости, линии тока становятся
волнистыми (точка перехода 2, переходная
зона-2), затем развивается устойчивое
турбулентное течение (зона 3).
В турбулентном ПС, однако, вблизи поверхности сохраняется весьма тонкий ламинарный подслой 4. Следует отметить, что в ТПС градиент скорости значительно выше по сравнению с ЛПС (фиг.28).
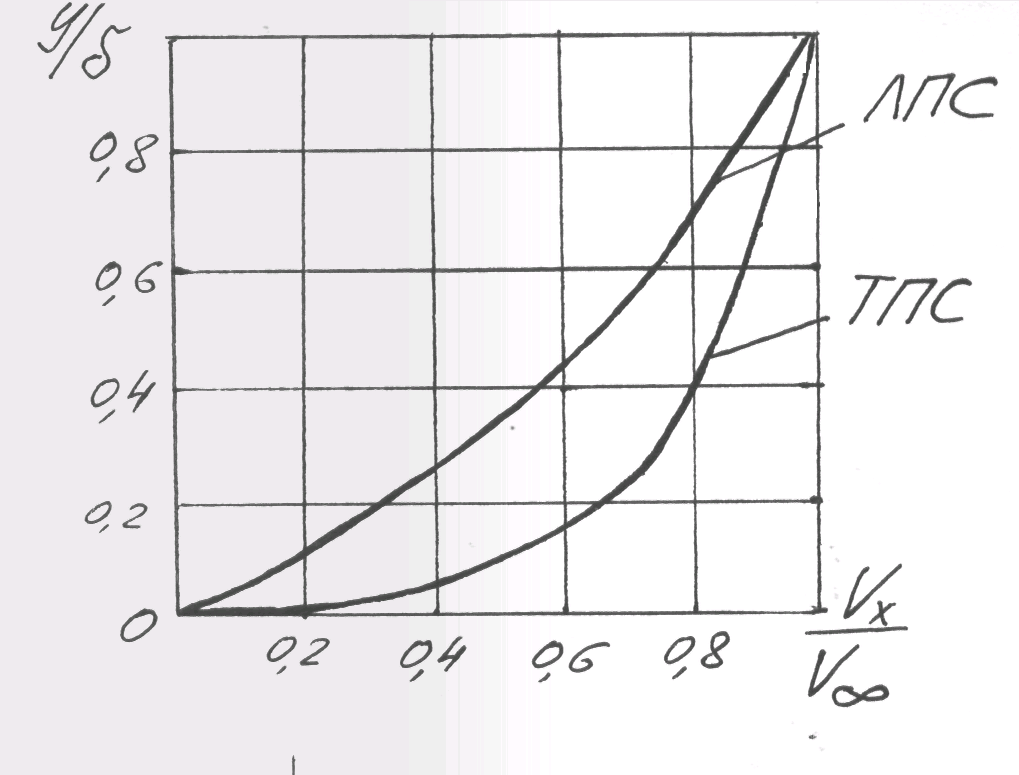
Фиг.28. Сравнение эпюр скорости в ламинарном и турбулентном пограничных слоях.
На обтекаемом теле ПС имеет примерно ту же структуру, что и на пластине (фиг.29).
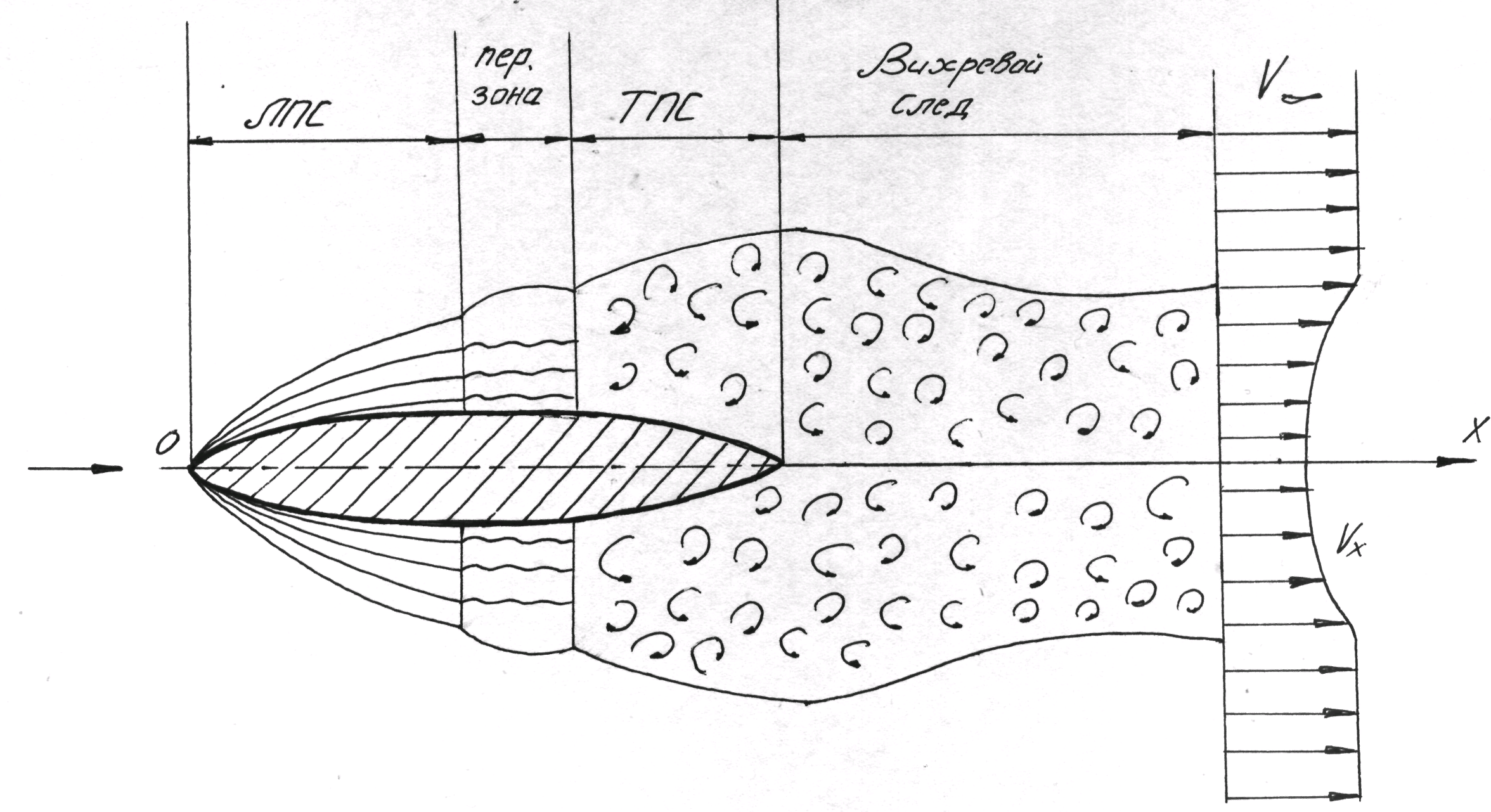
Фиг.29 Схема потока при обтекании тела вязкой жидкостью.
За обтекаемым
телом пограничные слои, образовавшиеся
на нижней и верхней поверхностях тела,
смыкаются и переходят в вихревой след,
который по мере удаления от тела
размывается («расплывается»), скорости
в нем выравниваются и вдали от тела
приближаются к скорости невозмущенного
потока
![]() .
.
8.3. Интегральное соотношение для установившегося течения в пограничном слое несжимаемой жидкости.
Рассмотрим течение жидкости в двумерном плоскопараллельном потоке над криволинейной поверхностью малой кривизны (фиг.30).
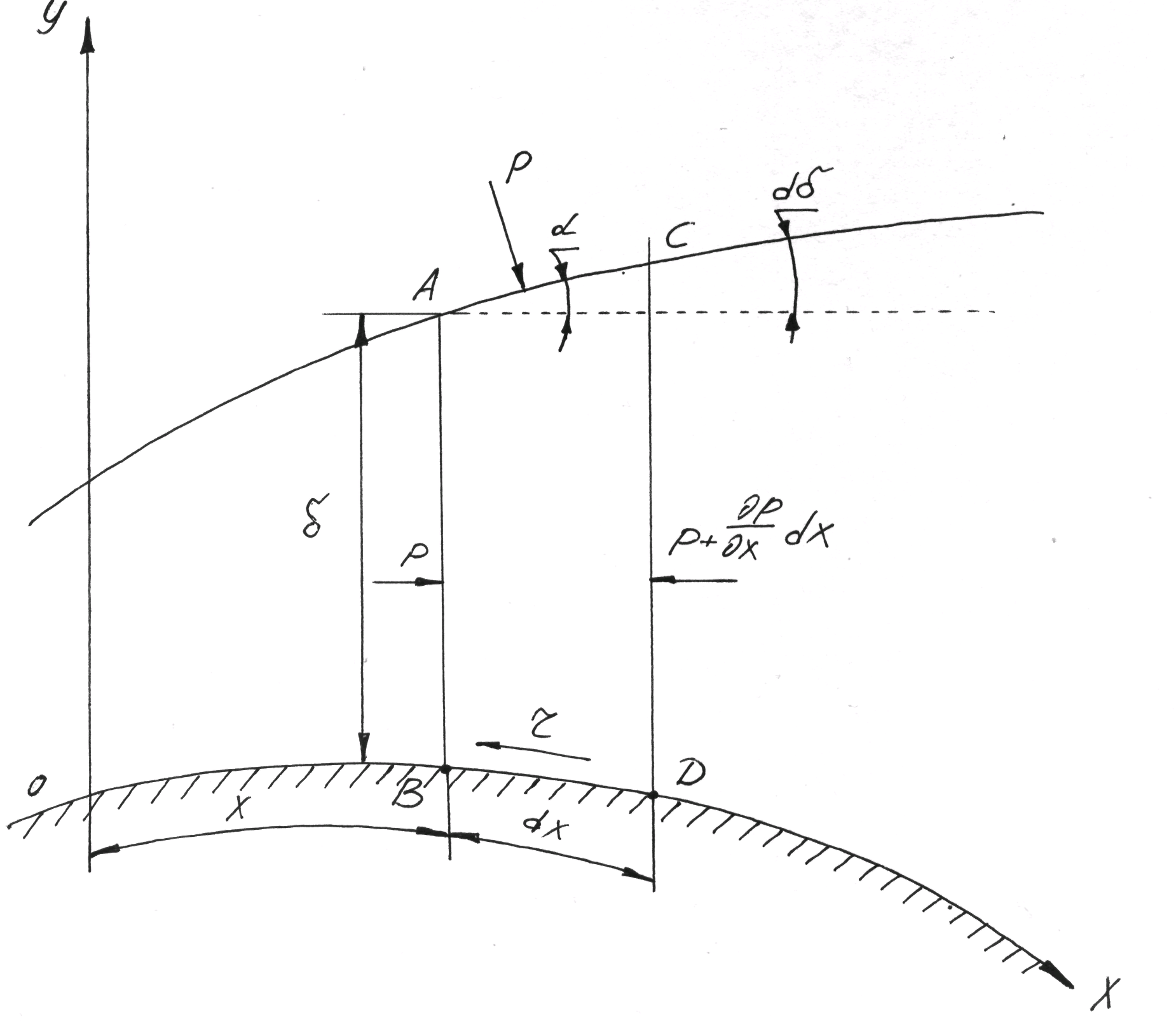
Фиг.30
В этом случае удобно ось координат ОХ считать криволинейной, расположив её на обтекаемой поверхности вдоль течения.
Проведем через
точки B
и D,
отстоящие на расстоянии
![]() друг от друга, нормали к контуру.
друг от друга, нормали к контуру.
Элементарная площадка ABDC с длиной является основанием выделенного из жидкости объема, шириной, равной 1-це. Применим к этому жидкому элементарному объему теорему об изменении количества движения (теорему импульсов), при этом количество движения и импульс действующих сил на этот элемент запишем только для проекции на ось ОХ.
Масса жидкости,
втекающая через сечение AB
за время
![]() с переменной по сечению скоростью, и
масса жидкости, вытекающая через сечение
СD
за это же время, соответственно равны:
с переменной по сечению скоростью, и
масса жидкости, вытекающая через сечение
СD
за это же время, соответственно равны:
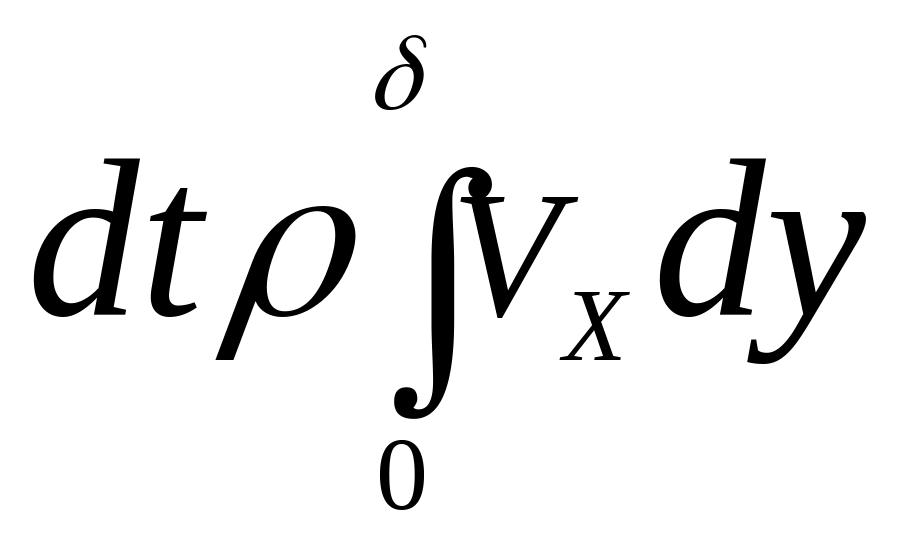 и
и
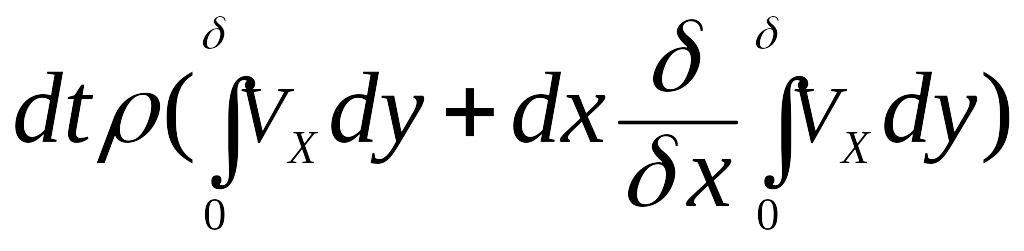 ,
откуда находим разность вытекающей и
втекающей масс жидкости-
,
откуда находим разность вытекающей и
втекающей масс жидкости-
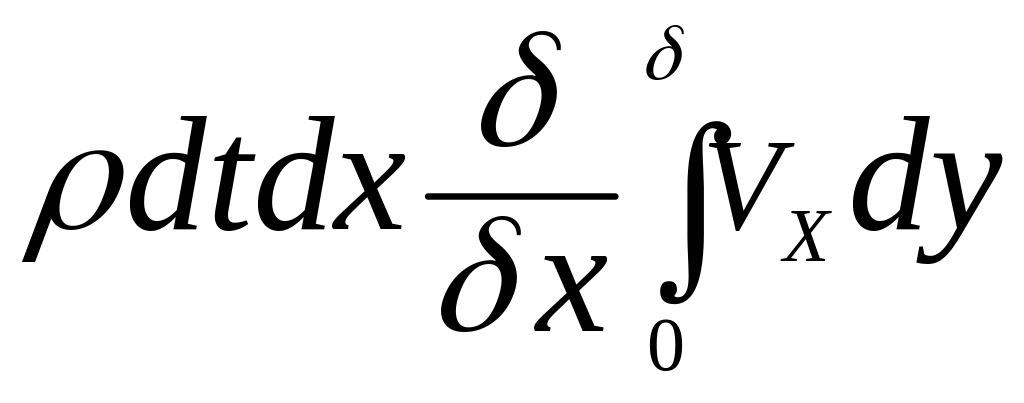 .
.
Проекция на ось
ОХ количества движения жидкости,
втекающей за время
![]() через сечение AB:
через сечение AB:
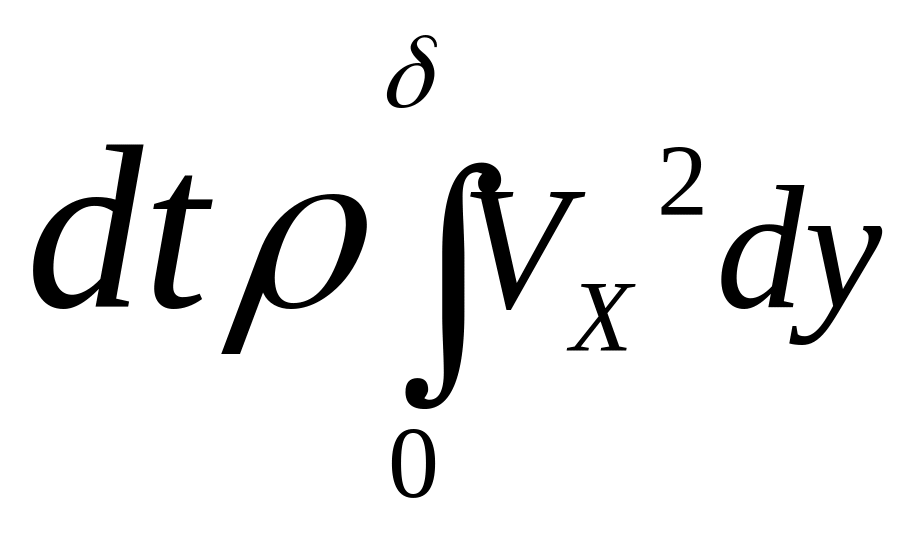 ,
а проекция количества движения жидкости,
вытекающей через сечение СD:
,
а проекция количества движения жидкости,
вытекающей через сечение СD:
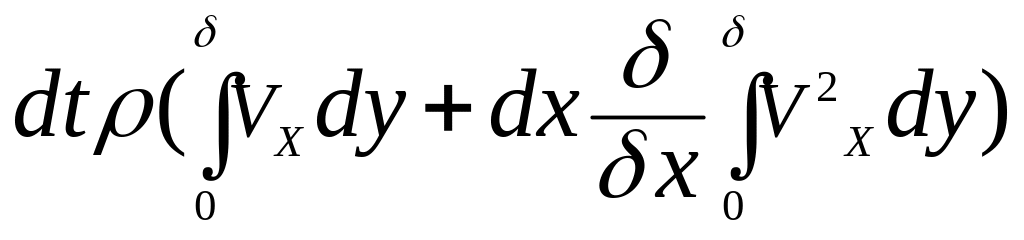 .
.
Из условия сохранения массы через верхнюю границу ПС АС внутрь объема ABCD должна втекать масса жидкости, равная разности масс жидкости, вытекающей через сечение СD и втекающей через сечение AB, т.е.
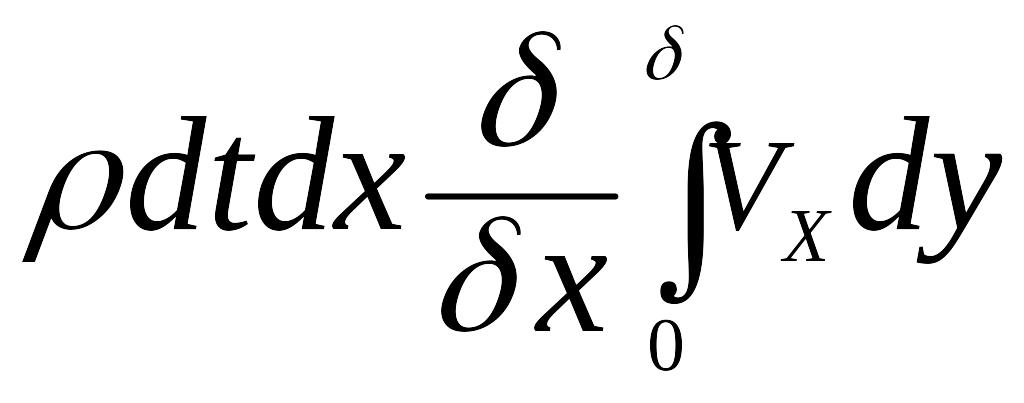 .
.
Количество движения,
вносимое этой жидкостью,
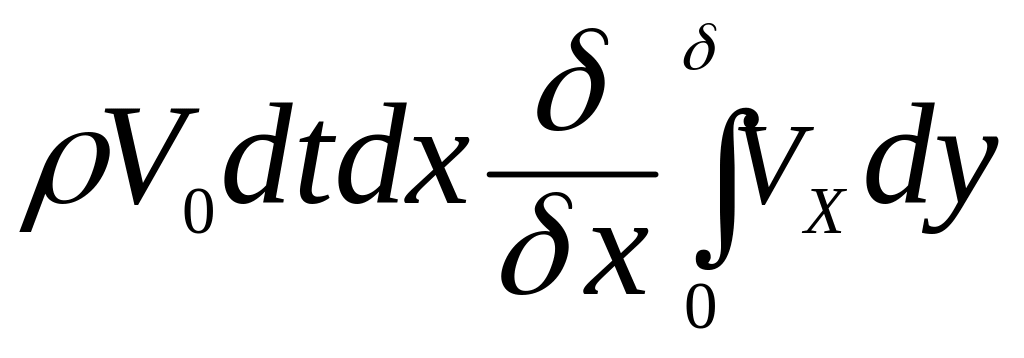 ,
где
,
где
![]() -
скорость на верхней границе ПС.
-
скорость на верхней границе ПС.
Таким образом, проекция на ось ОХ приращения количества движения жидкости, находящейся в момент времени t внутри объема ABCD за время равно:
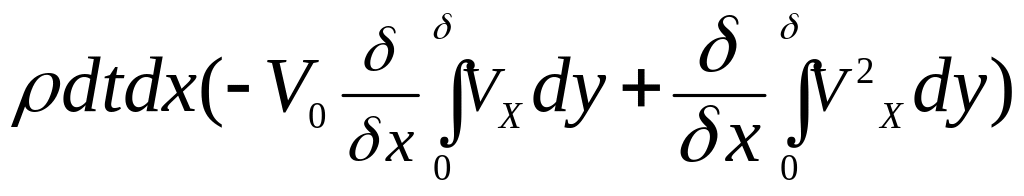 (а).
(а).
Количество движения,
вносимое в объем ABCD
за время
![]() ,
считаем отрицательным, а уносимое из
этого объема – положительным.
,
считаем отрицательным, а уносимое из
этого объема – положительным.
Вычислим проекцию на координатную ось ОХ суммы импульсов внешних сил, действующих за время на жидкость, заключенную внутри элементарного объема ABCD.
Проекции на ось ОХ внешних сил (сил давления), действующих на грани AB, AC и DC будут соответственно равны:

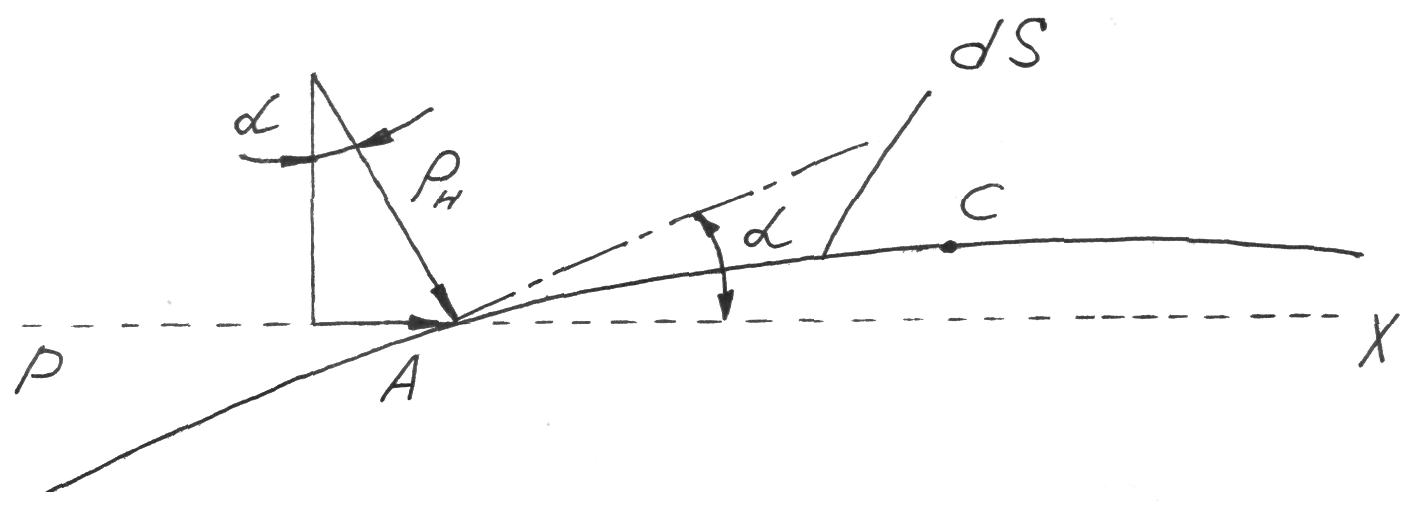
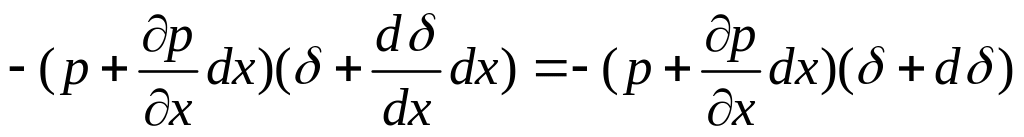 ,
где
,
где
 между АС и осью ОХ.
между АС и осью ОХ.
Пренебрегая малыми величинами высшего порядка и учитывая, что проекция силы давления на плоскость элемента стенки BD на ось ОХ равна 0, получим сумму проекций сил давления на ось ОХ:
![]() Тогда
проекцию импульса сил давления на ось
ОХ можно записать как
Тогда
проекцию импульса сил давления на ось
ОХ можно записать как
 (б)
(б)
Импульс силы
трения, приложенной к нижней грани BD,
площадь которой
![]() ,
имеет проекцию на ОХ равную:
,
имеет проекцию на ОХ равную:
![]() ,
где
,
где
![]() -
касательное напряжение (в).
-
касательное напряжение (в).
Учитывая, что
изменение количества движения равно
импульсу сил, приравниваем сумму (а) к
сумме выражений (б), (в) и после сокращения
на
![]() получим:
получим:
 .
(44)
.
(44)
Это равенство, полученное на основании теоремы механики о количестве движения, называется уравнением импульсов или интегральным соотношением Кармана для плоского установившегося течения в ПС несжимаемой жидкости. С помощью (44) можно определить толщину ПС и распределение сил трения по поверхности тела.
Кроме того, интегральное соотношение (44) применимо и для ламинарного, и для турбулентного пограничных слоев.
Учитывая, что в уравнении (44) в силу стационарности течения все величины зависят только от координаты Х, частные производные можно заменить полными:
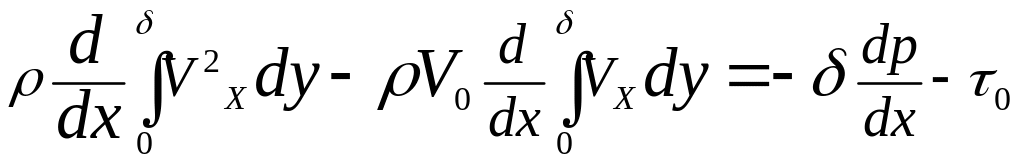 (45).
(45).
B
уравнении (45) известными считаются
величины
![]() ,
,
![]() (из уравнения Бернулли
(из уравнения Бернулли
 ),
плотность
,
а неизвестными -
),
плотность
,
а неизвестными -
![]() и
и
![]() .
Поэтому для решения конкретных задач
необходимо иметь еще 2 соотношения,
например:
.
Поэтому для решения конкретных задач
необходимо иметь еще 2 соотношения,
например:

