8. Ламинарный и турбулентный пограничные слои.

8.1. Основные понятия пограничного слоя.

При обтекании тел потоком реальной (вязкой) жидкости или газа с большими числами Re (Re 1) возникают турбулентные пульсации (о чем говорилось выше) и, в частности, величины градиента скорости dV_x /dy достигают больших значений. В этих областях в непосредственной близости у поверхности тела на характер течения существенное влияние оказывают силы внутреннего трения жидкости, обусловленные наличием вязкости.

Тонкий по сравнению с характерным линейным размером тела слой газа (жидкости), прилегающий к твердой поверхности, в котором градиенты газодинамических переменных (V,,Т) в нормальном к стенке направлении (по оси OY ) значительно превышают градиенты этих величин в касательных направлениях (по осям OX, OZ ) , а инерционные и вязкие силы имеют один и тот же порядок, называется пограничным слоем (ПС).

Вне ПС влияние сил вязкости пренебрежительно мало, и течение определяется в основном силами давления и массовыми силами. В ПС скорость изменяется от нуля (жидкость, обладая вязкостью, прилипает к поверхности тела) до величины, имеющей место в идеальной жидкости. При внешнем обтекании, по мере удаления от передней критической точки тела к задней, кромке толщина ПС возрастает.

Глубокие теоретические и экспериментальные исследования показали, что без участия ПС не могут возникнуть циркуляция и подъемная сила крыла.

Без понимания структуры и характера течения жидкости(газа) в ПС невозможно объяснить такие важные аэродинамические явления, как возникновение срыва потока на хорошо обтекаемых, казалось бы телах, а также определить силы трения газа на поверхности тела. Толщина и характер ПС определяют процессы переноса количества движения, энергии, массы между потоком жидкости и телом. Теория ПС лежит в основе таких курсов, как гидравлика, газодинамика, тепло-массообмен.

Рассмотрим вначале простейший случай – течение вязкой жидкости около плоской пластины (фиг.25).

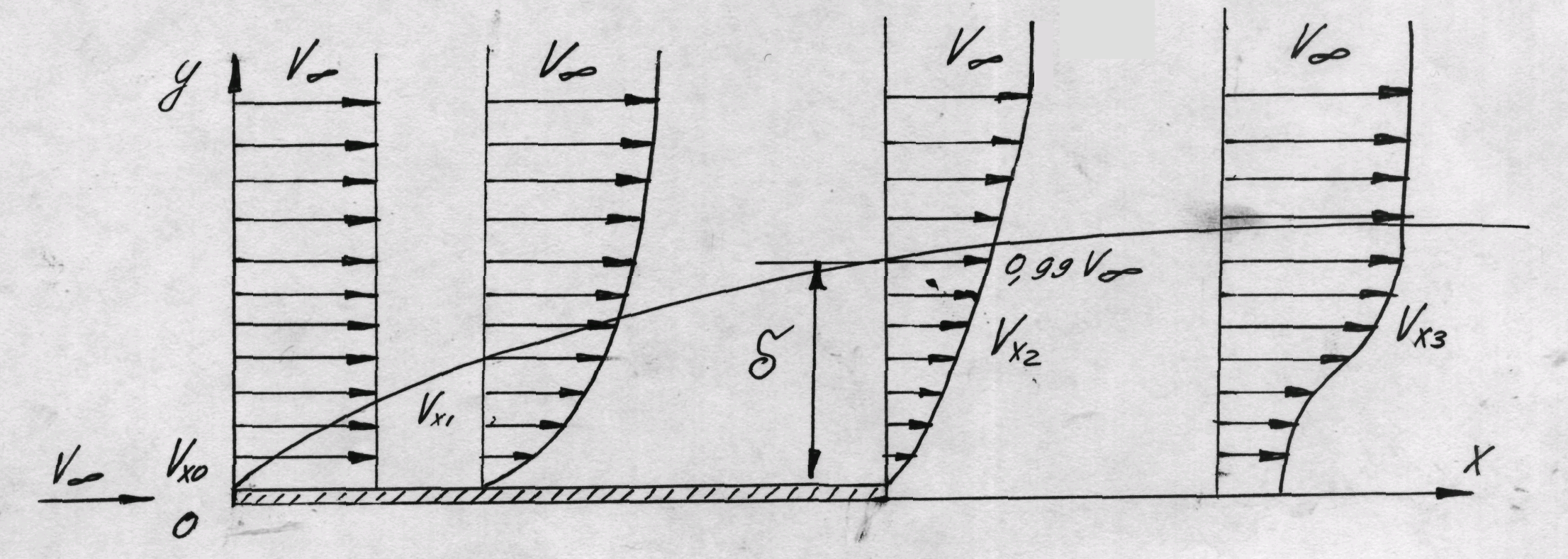
Фиг.25

Опыты показывают, что частицы жидкости, соприкасающиеся с поверхностью пластины, полностью затормаживаются. По мере удаления от пластины скорость течения увеличивается, асимптотически приближаясь к теоретической скорости, соответствующей обтеканию тела невязкой жидкостью. В нашем случае – к скорости внешнего невозмущенного потока ( ). Это обстоятельство делает неопределенным положение верхней границы ПС и затрудняет определение его толщины, т.е. строго говоря, конечной толщины ПС не существует.

Имеется несколько примеров определения толщины ПС. Согласно одному из них, толщина ПС определяется как расстояние от поверхности тела по нормали (по оси ОУ) до значения, в котором местная скорость потока .

В соответствии с принятым определением толщины ПС внешняя граница ПС не является линией тока и служит лишь условным пределом зоны влияния вязкости. Поэтому в современной теории ПС чаще всего пользуются понятиями толщины потери импульса и толщины вытеснения , которые косвенным образом характеризуют поперечный размер ПС, но определяются более точно, чем толщина ПС.

Рассмотрим физический смысл этих толщин:

1. Толщина потери импульса:

Выражение для толщины потери импульса имеет вид: (37),

где - толщина потери импульса;

- толщина ПС;

- переменная по высоте y скорость течения в ПС;

- скорость на границе слоя и потока.

Определение: Толщина потери импульса представляет собой такую толщину ПС, которая при умножении на плотность и квадрат скорости на внешней границе слоя дает разницу между количеством движения массы жидкости, текущей в ПС со скоростью, равной скорости на внешней границе слоя, и действительным количеством движения в слое.

Для случая обтекания пластины, поставленной вдоль потока, на основании теоремы механики о количестве движения (изменение количества движения равно импульсу сил: ), получено следующее выражение для толщины потери импульса:

(38).

Сила сопротивления трения, развивающаяся на обеих сторонах пластины длиной l, получится интегрированием выражения (38):

(39), где - толщина потери импульса на конце пластины.

Отметим, что речь идет об элементарной площади шириной . Равенство (39) логично рассматривать как уравнение изменения количества движения (импульса) , пропорционального величине , т.е. потери, обусловленные силой трения. Этим объясняется термин “толщина потери импульса”.

2. Толщина вытеснения :

Рассмотрим обтекание невозмущенным потоком вязкой жидкости пластины, поставленной параллельно вектору скорости потока (фиг. 26).

Фиг. 26 Отклонение линий тока вблизи плоской пластины

вследствие образования ПС.

Пусть граница ПС ОА определяется его толщиной . Линии тока невозмущенного потока перед пластиной (x < 0) представляют собой параллельные пластине прямые, однако над пластиной (х > 0) они должны отклоняться. Действительно, поскольку в сечении mn, где толщина ПС , скорости всюду меньшие, чем скорость невозмущенного потока, расход жидкости через это сечение будет меньше, чем через сечение ab того же размера , проведенное в невозмущенном потоке. Поэтому линия тока перед пластиной, чтобы обеспечить пропуск расхода , должна отклониться на некоторую величину .

Тогда уравнение баланса расходов для сечений ab и mn запишем в виде:

(40).

Здесь слагаемое выражает расход через сечение , в котором продольная составляющая скорости (вдоль оси ОХ) практически равна .

Т.к. , из уравнения (40) можно определить толщину вытеснения:

(41).

Из анализа (41) видно, что толщина вытеснения представляет собой отклонение линии тока вязкой жидкости от линий тока идеальной жидкости, которое вызвано тормозящим действием твердой поверхности, т.е. образованием ПС.

Важно отметить, что величина практически не зависит то точности определения , т.к. начиная с некоторых значений расстояния от пластины .

Рассматривая понятия толщины вытеснения на частном примере обтекания пластины, оно сохраняет свой смысл и для обтекания других поверхностей.

Принимаем, что , однако при больших Re (скачок уплотнения), поэтому справедливо следующее утверждение.

Вытесняющее действие ПС состоит в том, что через его сечение, за счет уменьшения скорости и плотности, протекает меньше реальной жидкости, чем протекало бы идеально, т.е. в том, что часть жидкости вытесняется за его границу во внешний поток. Это приводит к появлению в ПС вертикальной составляющей V_y скорости V. Из-за малой относительной толщины ПС угол наклона линий тока очень мал, следовательно, составляющая V_y при обтекании плоской пластины очень мала и не сопоставима с горизонтальной составляющей (V_x>>V_y). Поэтому изменение количества движения жидкости в ПС в направлении оси OY практически отсутствует. Отсюда мы приходим к важнейшему выводу теории ПС – статическое давление поперек ПС не изменяется:

.

Толщина вытеснения есть расстояние, на которое отодвигается от тела линия тока внешнего течения в результате вытесняющего действия ПС.

Иначе, толщина вытеснения - это толщина слоя, в каждом сечении которого (b=1, т.е. для элементарной площадки) расход невозмущенного потока равен расходу, вытесненному из ПС в соответствующем сечении , т.е.

.

Учитывая, что  , получаем:

(42).

Уравнение (42) аналогично (41), но учитывает изменение .

То же самое и для толщины потери импульса при .

Толщина потери импульса - это толщина слоя, в каждом сечении которого газ с параметрами невозмущенного потока проносит секундное количество движения, равное потерянному жидкостью, текущей в ПС, за счет уменьшения скорости (из-за трения).

Приняв секундное количество движения газа в слое толщиной , равное

,

т.е. уменьшению секундного количества движения массы жидкости, текущей в ПС, получим:

^, т.е.

(43).

Уравнение (43) аналогично (37), но учитывает изменение .