7.2. Сжимаемость газов. Скорость распространения звука в газе.

Отличительным свойством газов является сжимаемость.

Определение. Сжимаемость – способность газа изменять свой объем (а, следовательно, и плотность) при изменении давления и температуры.

Предположим, что изменение давления на вызывает изменение плотности на . При этом сжимаемость газа характеризуется отношением . Чем больше при заданном (чем меньше отношение ), тем больше сжимаемость газа. Предел этого отношения при равен квадрату скорости распространения малых возмущений или квадрату скорости звука:

(24)

Следовательно, скорость распространения звука может служить мерой сжимаемости газовой среды под воздействием малых давлений.

В несжимаемой среде . Для изоэнтропических течений: , где (для воздуха) – показатель изоэнтропы. Тогда:

(25).

Учитывая уравнение состояния (уравнение Менделеева - Клайперона): , выражение (25) можно представить: (26), где - удельная газовая постоянная.

При постоянных значениях k и скорость звука в газе зависит от его абсолютной температуры: .

Таким образом, в сжимаемой среде малые возмущения распространяются с конечной скоростью , зависящей от температуры.

В аэродинамике часто скорость звука используют для получения безразмерной скорости газа:

– число Маха – отношение скорости потока к местной скорости звука. Для абсолютно несжимаемой среды М = 0. Влияние сжимаемости на характеристики течения газа начинает сказываться на скоростях при М = 0.4…0.5 и растут с ростом М, вызывая не только количественные, но и качественные изменения характеристик течения при звуковых (М = 1) и сверхзвуковых (М больше 1) скоростях. При малых скоростях ( ) влиянием сжимаемости воздуха логично пренебречь и рассматривать его как несжимаемую среду, полагая .

Определим физический смысл числа Маха. Рассмотрим совместно уравнение неразрывности: и уравнение Бернулли в дифференциальной форме:

(27).

Известно, что дифференциал произведения равен: . Поделим на :

.

В случае несжимаемой среды ( ) из уравнений (24) и (27) получаем:

или .

Введем число Маха: . Следовательно, число Маха с физической точки зрения характеризует относительное изменение плотности газовой среды на единицу относительного изменения скорости потока. Т.е. число Маха, также как и скорость звука, является характеристикой сжимаемости потока газа.

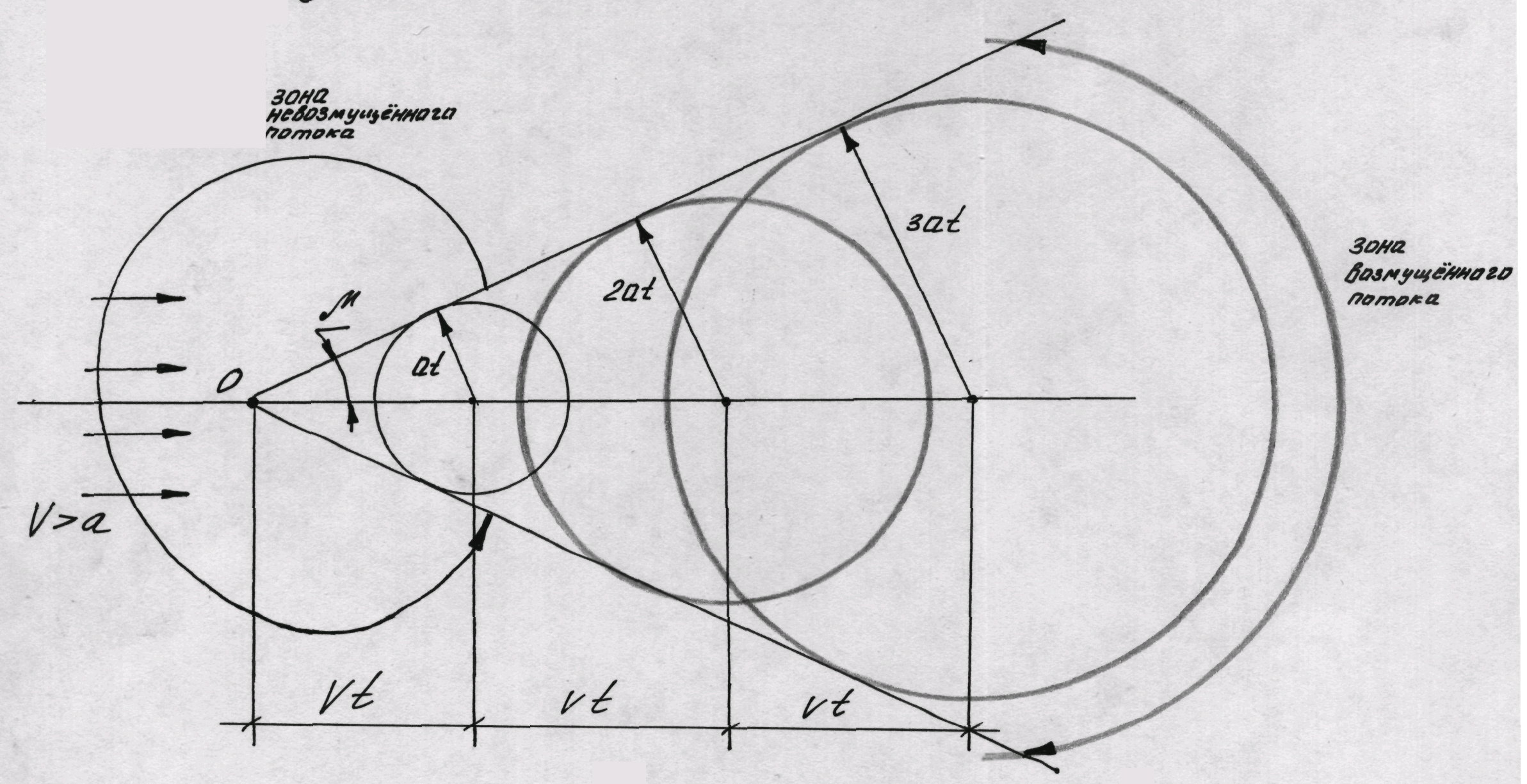
Предположим, что в неподвижной газовой среде находится точечный источник периодических слабых (акустических) возмущений, которые распространяются со скоростью звука, вследствие этого возникает семейство расширяющихся концентрических поверхностей с центром в источнике возмущений. (Фиг. 20).

Фиг. 20 Распространение слабых возмущений в неподвижной среде.

Представим теперь, что источник возмущений неподвижен, а среда движется относительно него со скоростью (Фиг. 21).

Фиг. 21 Распространение слабых возмущений в дозвуковом потоке.

За время между двумя сигналами первая волна будет смещена по потоку, и центры сферических волн окажутся смещенными относительно друг друга на величину . Поскольку , волны между собой пересекаться не будут.

Иначе обстоят дела при (сверхзвуковой поток), здесь семейство сферических волн приобретает огибающую в виде конуса (Фиг. 22).