6.3. Геометрический и энергетический смысл уравнения Бернулли.

6.3.1. Геометрический смысл уравнения Бернулли.

Для пояснения смысла каждого из членов уравнения Бернулли обратимся к вышеприведённой диаграмме, на которой показана элементарная струйка движущейся жидкости. Предположим, что в сечениях 1,2,3, расположенных на высотах от плоскости сравнения О-О установлены пьезометрические трубки. Вследствие наличия в точках установки пьезометров давления, жидкость в каждой трубке поднимется на высоту , которая также как и в гидростатике называется пьезометрической.

6.3.2. Физический смысл уравнения Бернулли.

Умножим все члены уравнения (19) на g. Тогда получим:

(20)

Удельная энергия жидкости – энергия, отнесенная единице массы, веса или объема.

Члены уравнения (20) являются различными формами удельной энергии жидкости, а именно:

1. - удельная энергия положения, т.к. частица жидкости массой m, находясь на высоте y, обладает энергией положения, равной , а на единицу массы приходится энергия ;

2. - удельная энергия давления движущейся жидкости, т.к. частица массой m при давлении p обладает способностью подняться на высоту (например в пьезометре) и приобрести энергию положения , после деления на m получаем . Таким образом получим: - удельная потенциальная энергия жидкости;

3. - удельная кинетическая энергия жидкости, т.к. для той же частицы m, кинетическая энергия, отнесенная к единице массы .

Таким образом, полная удельная механическая энергия движущейся жидкости равна - гидродинамический напор.

Следовательно, каждый член уравнения Бернулли представляет собой удельную потенциальную или кинетическую энергию жидкости в сечении потока.

Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии жидкости. Уравнение Бернулли выражает закон сохранения механической энергии в идеальной жидкости. Механическая энергия движущейся жидкости может иметь три формы: энергия положения, энергия давления и кинетическая энергия. Первая и третья формы механической энергии известны из механики и они в равной степени свойственны твердым и жидким телам. Энергия давления является специфической для движущейся жидкости. В процессе движения жидкости одна форма энергии может превращаться в другую, однако полная удельная энергия при этом, как следует из уравнения Бернулли, остается без изменений.

Уравнение Бернулли часто пишут еще и в третьей форме. Разделив все члены уравнения (19) на объем , после преобразования ( ) получим:

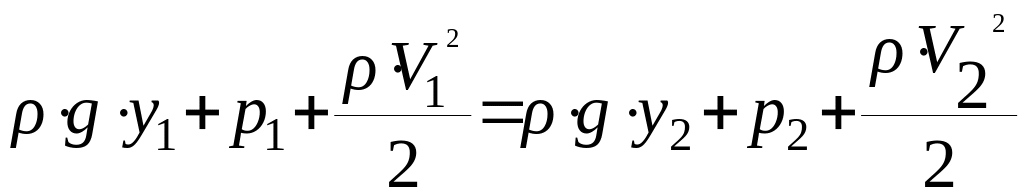(21)

Теперь члены уравнения Бернулли имеют размерность давления (Па) и называются:

- весовое давление; p – статическое давление; - динамическое давление.

Члены уравнения (21) представляют собой различные формы механической энергии жидкости, отнесенные к единице ее объема.

6.4. Уравнение Бернулли для потока реальной (вязкой) жидкости.

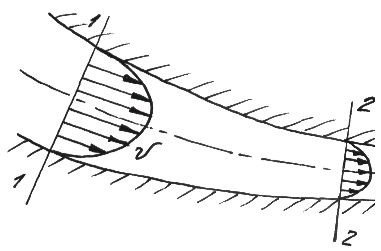
При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему конечные размеры и ограниченному стенками, необходимо учитывать неравномерность распределения скоростей по сечению, а также потери энергии (напора). То и другое является следствием вязкости жидкости. При движении вязкой жидкости вдоль твердой стенки из-за вязкости происходит торможение потока. Поэтому наибольшего значения скорость достигает в центральной части потока, а по мере приближения к стенке она уменьшается практически до нуля. Эпюра скоростей имеет примерно такой (см. рис. ) вид.

Неравномерное распределение скоростей означает скольжение (сдвиг) одних слоев жидкости по другим, вследствие чего возникают касательные напряжения (напряжения трения). Кроме того, движение вязкой жидкости сопровождается вращением частиц, вихреобразованием, отрывами и перемешиванием. Все это требует затрат энергии, поэтому удельная энергия жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений (часть переходит в тепловую энергию) и, следовательно, уменьшается вдоль потока.

Из-за неравномерного распределения скоростей приходится вводить среднюю по сечению скорость , имеющую размерность

Возьмем два сечения реального потока: первое (1-1) и второе (2-2), и обозначим средние значения полного напора ( ) жидкости в этих сечениях соответственно . Тогда , где - суммарная потеря полного напора между сечениями 1 и 2.

Учитывая это, уравнение Бернулли для потока вязкой жидкости имеет следующий вид:

(22),

где коэффициенты и - безразмерные коэффициенты Кориолиса, учитывающие неравномерность распределения скоростей, которые в общем виде записываются следующим образом: (23) - коэффициент неравномерности распределения скоростей по живому сечению потока.

Если умножить числитель и знаменатель (23) на , то нетрудно убедиться, что коэффициент представляет собой отношение действительной кинетической энергии потока жидкости, которую проносит поток через данное сечение в единицу времени (т.е. реальная мощность потока), к мощности потока в том же сечении, но при равномерном распределении скоростей.

Покажем это, учитывая ; , предположив, что V по сечению равна V_ср.

.

Проверим размерность: [ ] = [ ] = [ ] = [Вт]

Обычно при прямолинейном турбулентном движении в трубах , при прямолинейном ламинарном движении в трубах . В криволинейных потоках может быть существенно большим.

Таким образом, уравнение Бернулли для потока вязкой жидкости от аналогичного уравнения для элементарной струйки идеальной жидкости отличается членом, представляющим собой потерю полного напора (h_п), и коэффициентом, учитывающим неравномерность распределения скоростей. Кроме того, скорости, входящие в это уравнение, являются средними по сечениям.

Графически уравнение (22) можно представить диаграммой подобно тому, как это делали для идеальной жидкости, но с учетом потери напора. Потеря напора является некоторой высотой, которая возрастает вдоль потока.

Если для струйки идеальной жидкости уравнение Бернулли представляет собой закон сохранения полной механической энергии, то для потока реальной жидкости оно является уравнением баланса энергий с учетом потерь. Энергия, теряемая жидкостью на рассматриваемом участке течения, разумеется на исчезает бесследно, а превращается в другую форму – тепловую. Т.к. удельная теплоемкость жидкостей велика по сравнению с потерями удельной энергии, а также ввиду того, что тепловая энергия непрерывно рассеивается, повышение температуры практически бывает малозаметно. Такие потери необратимы, т.е. обратное превращение тепловой энергии в механическую невозможно.