6.2. Дифференциальные уравнения движения идеальной жидкости (уравнение Бернулли).

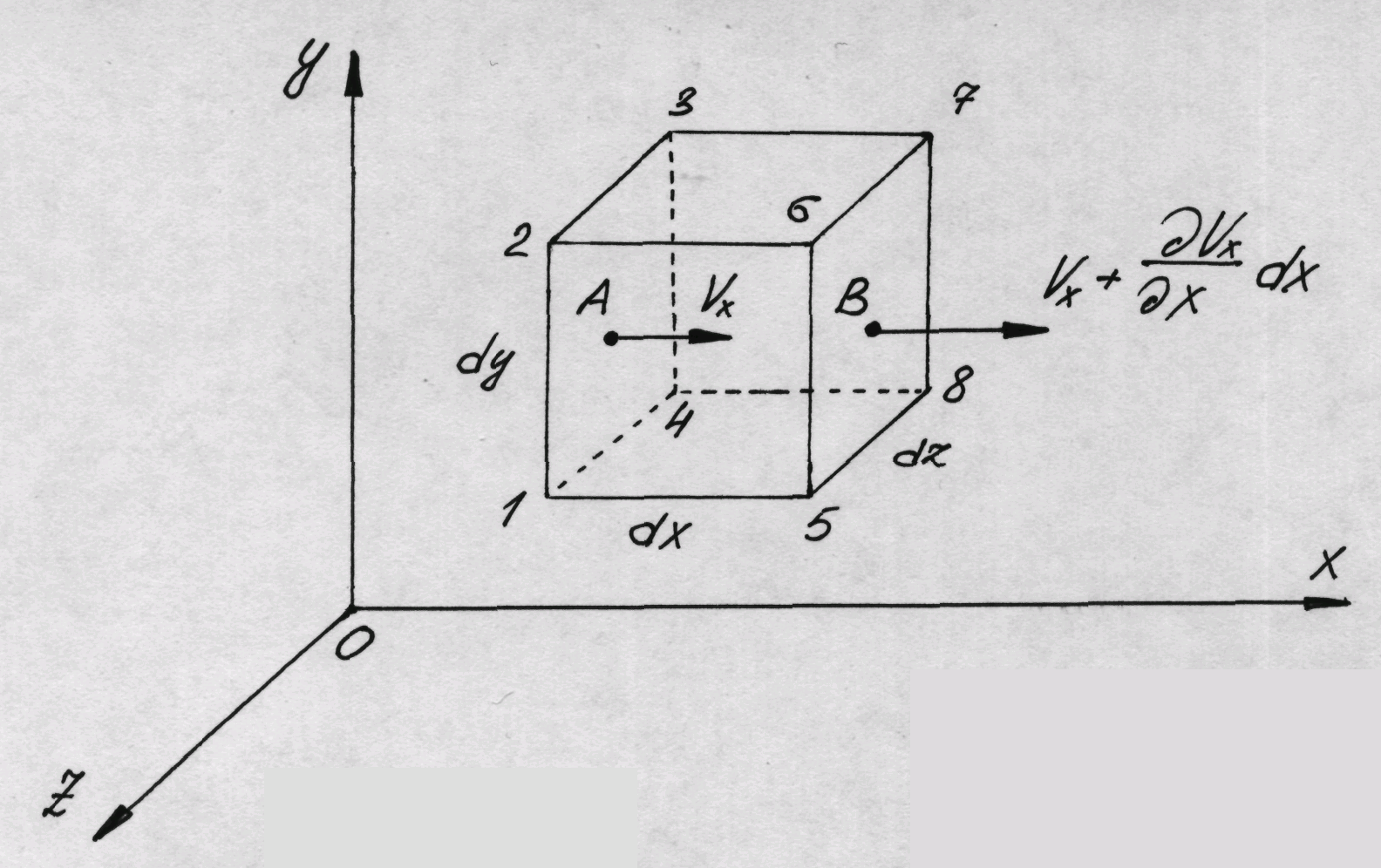
Рассмотрим движущуюся невязкую жидкость, у которой плотность ρ. Выделим в ней элементарный параллелепипед с рёбрами dx, dy, dz, параллельными к координатным осям. Составим уравнения движения выделенного элемента жидкости массой ρdxdydz в проекциях на координатные оси.

Также, как и при рассмотрении уравнения неразрывности объёма жидкости, будем считать, что на массу жидкости действует результирующая массовая сила (например, сила тяжести), составляющие которой, отнесённые к единице массы, равны x, y, z. Тогда массовые силы, действующие на выделенный объём в направлении координатных осей, будут равны этим составляющим, умноженным на массу выделенного объёма.

Кроме того, на массу жидкости в объёме параллелепипеда действуют поверхностные силы давления, окружающие жидкость, распределённые по граням параллелепипеда, направленные по внутренним нормалям к граням.

Обозначим p давление в произвольной точке с координатами x, y, z на левой вертикальной грани. Учитывая, что в сплошной жидкой среде давление есть непрерывная функция координат точек жидкости и времени p=f(x,y,z,t), поэтому, в силу сплошности среды и непрерывности функции давления в точке на правой грани с координатами (x+dx, y ,z), давление равно 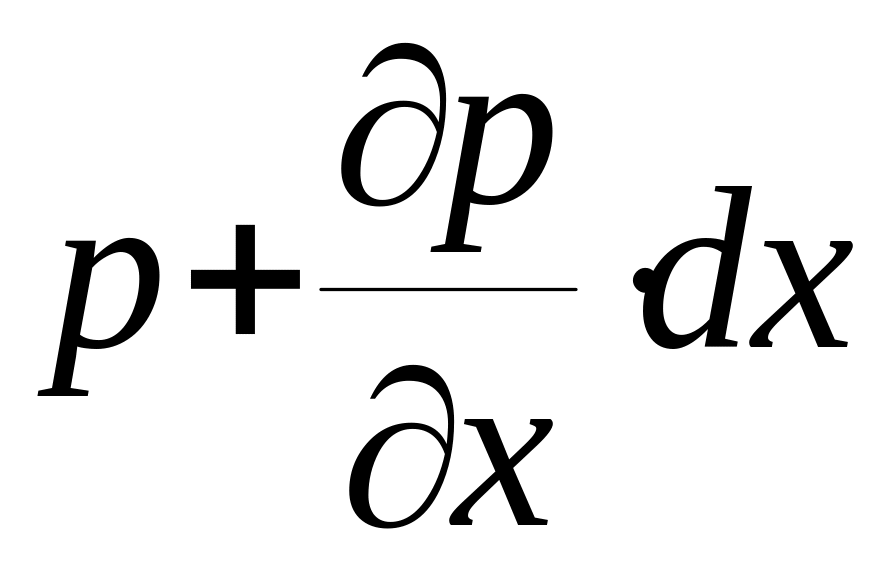с точностью до бесконечно малых второго порядка.

Разность давлений будет одинаковой для любой пары выбранных на этих гранях точек с одинаковыми координатами y, z, при этом проекция на ось OX результирующей силы давления равна

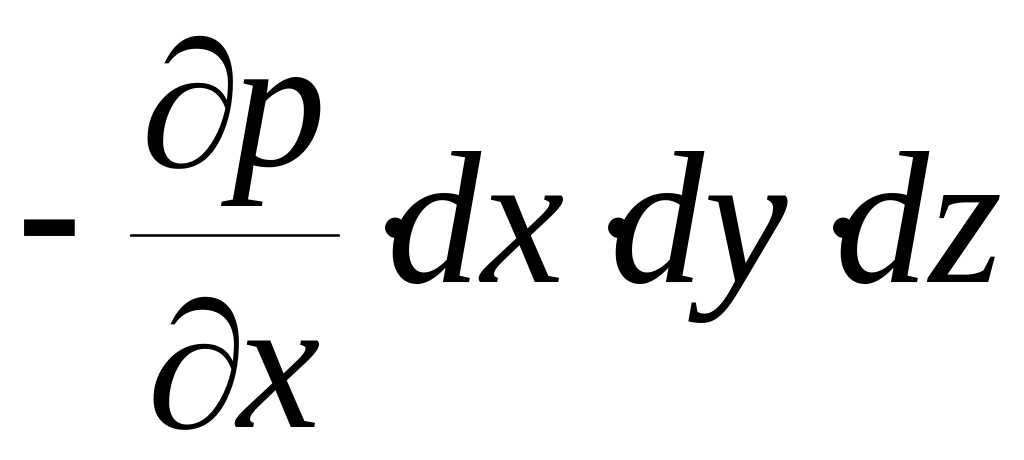
Скорость движения объёма обозначим через V, а её компоненты – V_x, V_y , V_z. Тогда проекции ускорения, с которым движется объём, равны:

, (16)

Согласно принципу Д’Аламбера, общие уравнения движения идеальной жидкости, могут быть получены из дифференциальных уравнений равновесия той же жидкости, если к действующим силам присоединить силы инерции, которые определяются, как произведение соответствующего ускорения (a_x, a_y, a_z) на массу параллелепипеда.

Уравнения движения объёма жидкости в проекциях на координатные оси имеют вид:

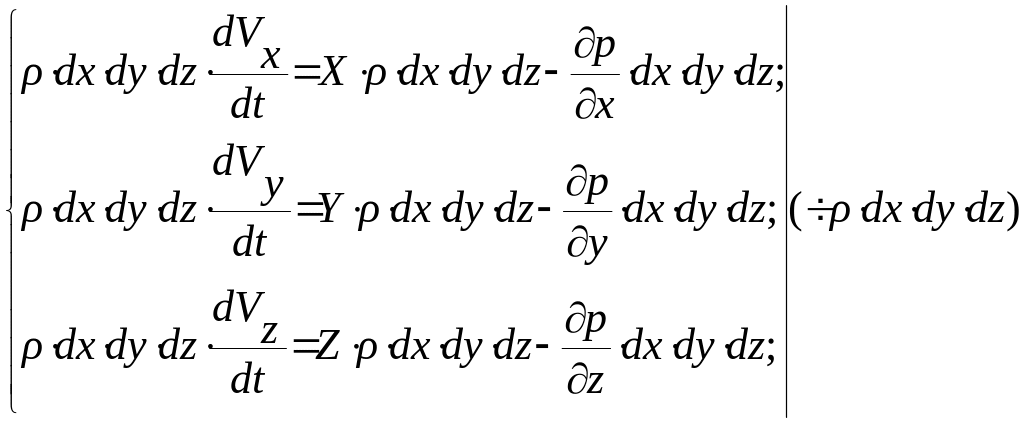(17)

Поделив уравнения (17) почленно на массу элемента , получим:

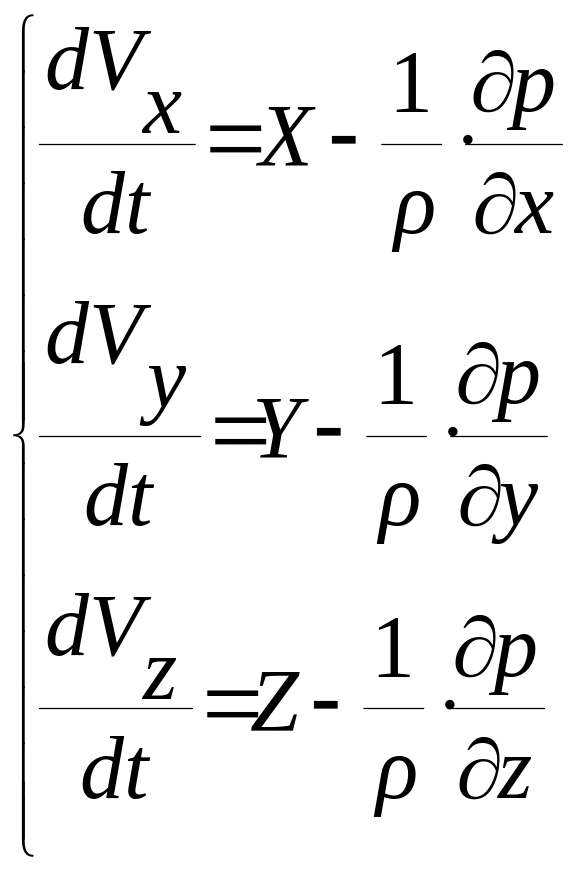– (18)

– система дифференциальных уравнений движения идеальной жидкости (система уравнений Эйлера, 1755 г.)

Члены этих уравнений представляют собой соответствующие ускорения, а смысл каждого из уравнений заключается в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления.

Рассматривая установившееся движение жидкости, умножим каждое уравнение (18) на соответствующие проекции элементарного перемещения, равные и сложим уравнения. Имеем:

.

Учитывая, что выражение в скобках является полным дифференциалом давления, а также, что

.

Получаем:

.

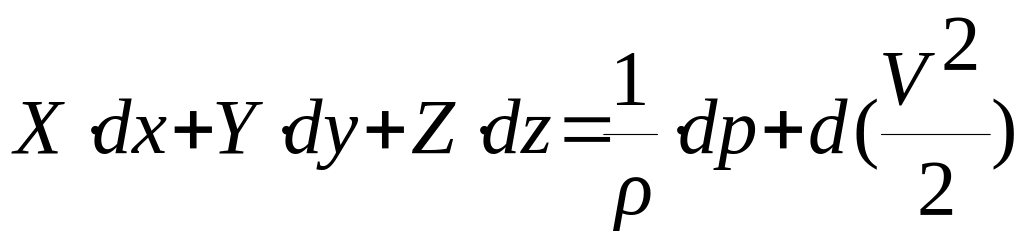Интегрирование этого уравнения выполним для случая установившегося движения идеальной жидкости, когда на жидкость действует лишь сила тяжести.

При направлении оси Y вертикально вверх: X=0; Y=-g; Z=0, следовательно:

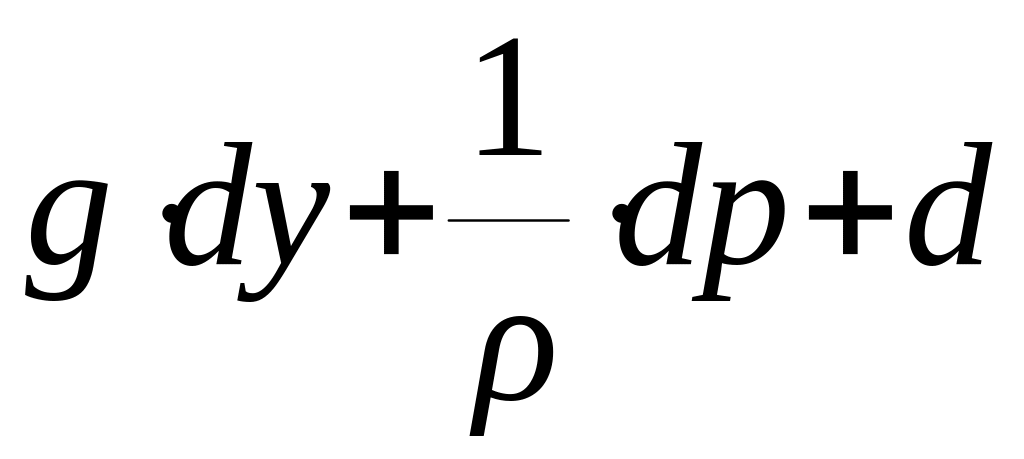
, следовательно:

.

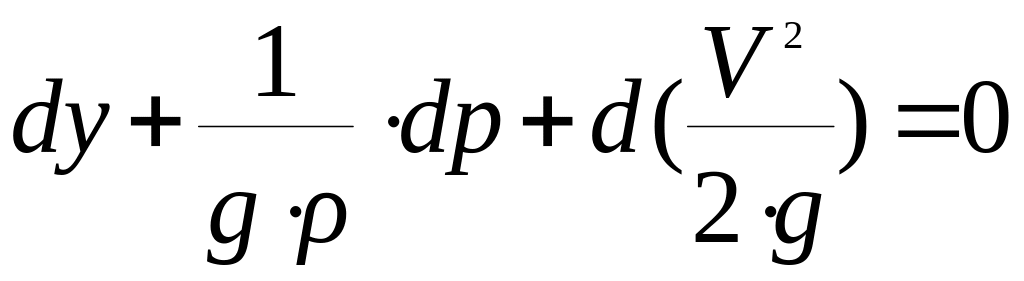Для несжимаемой жидкости , уравнение можно переписать в виде:

.

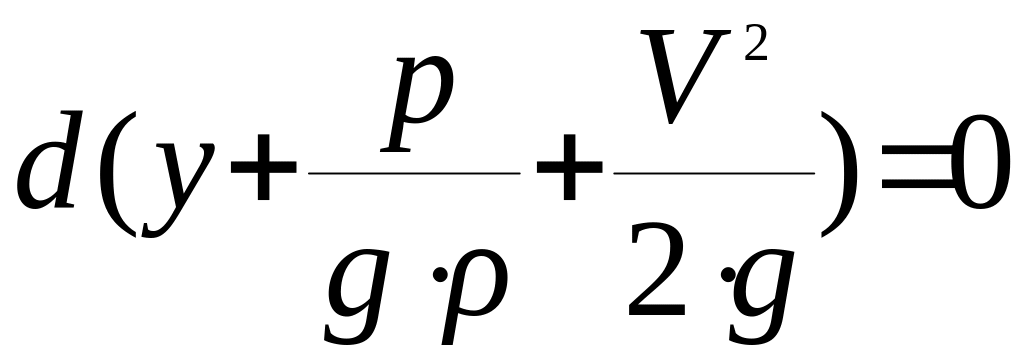Это уравнение означает, что приращение суммы трех членов, заключенных в скобки, при перемещении частицы жидкости вдоль линии тока (траектории) равно нулю. Следовательно, указанный трехчлен есть величина постоянная вдоль линии тока, а следовательно, и вдоль элементарной струйки, т.е.

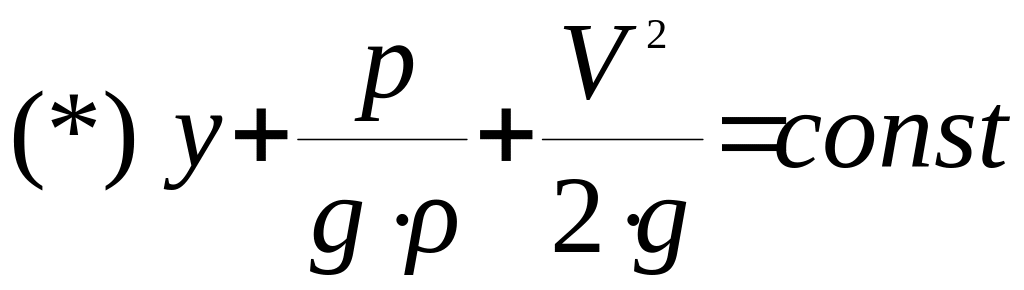– уравнение Бернулли для струйки идеальной жидкости.

Для двух сечений элементарной струйки идеальной жидкости можно записать уравнение Бернулли в другой форме:

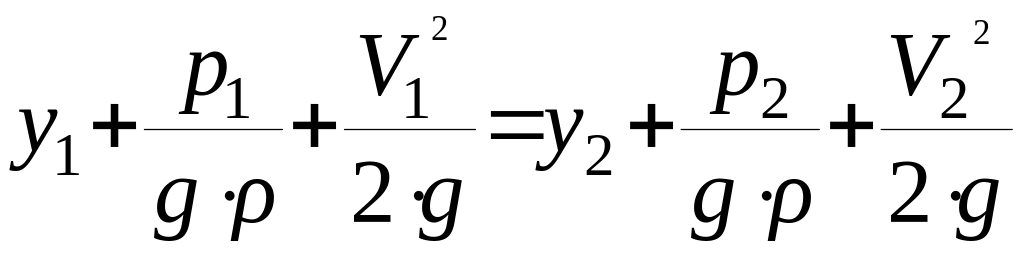(19)

(19) – уравнение Бернулли для элементарной струйки идеальной несжимаемой жидкости (1738 г.),

где - геометрическая высота или геометрический напор;

– пьезометрическая высота или пьезометрический напор;

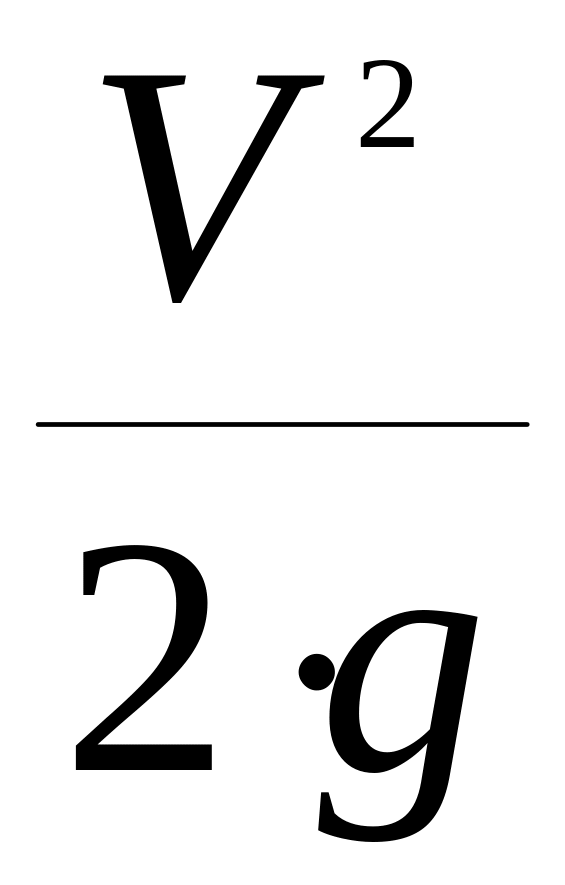– скоростная высота или скоростной напор.

Трехчлен вида 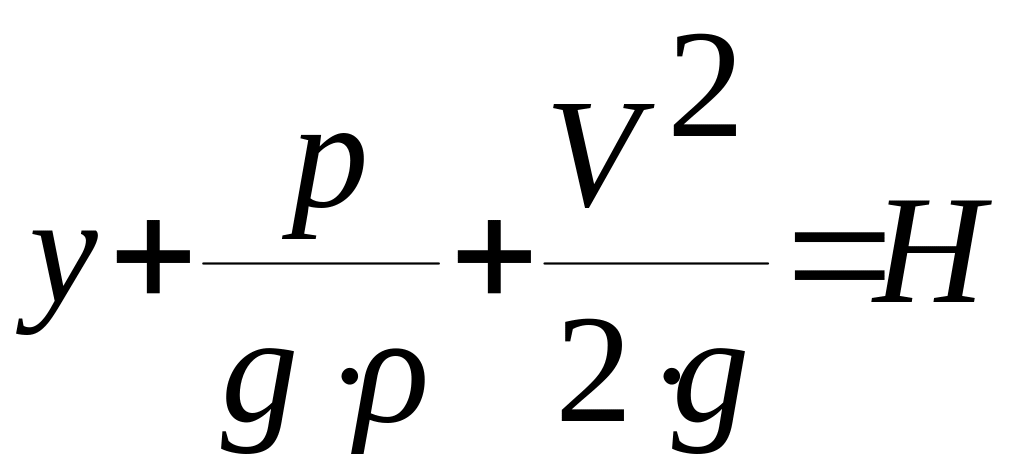- называется полным напором.

Уравнение Бернулли (19) записано для двух произвольно взятых сечений струйки и выражает равенство полных напоров в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение (см. уравнение (*)):

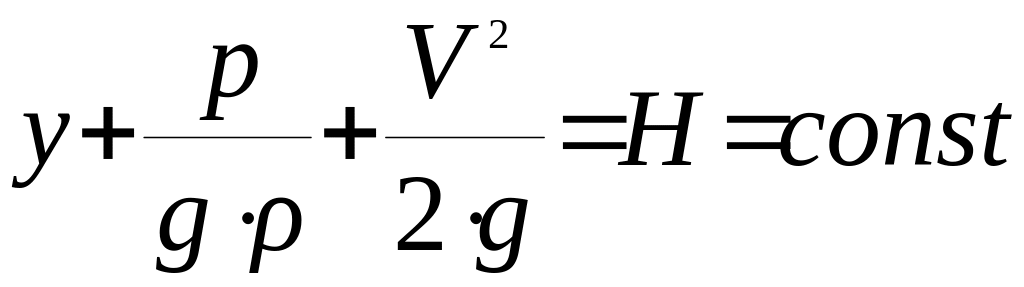(вдоль струйки).

Итак, для идеальной движущейся жидкости сумма трех напоров (высот): геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.