4.2 Задачи с решениями
Задача 4.2.1. По трубопроводу диаметром d = 150 мм перекачивается нефть в количестве 15 л/сек. Требуется определить: режим движения при температуре 10 0С; критическую скорость при той же температуре.
Решение. Определим среднюю скорость движения нефти по трубопроводу:
υ = Q / = 4Q / d2 = 0,85 м/сек = 85 см/сек.
Вычислим число Рейнольдса:
Re = υ d / = 3070 > 2300.
Так как Re > Reкр.н, то движение в нефтепроводе будет происходить в переходной области. Установим по формуле значение нижней критической скорости:
υ кр.н. = (Reкр.н·) / d = 64 см/с.
Задача 4.2.2. Пусть водомер Вентури имеет размеры D= 200 мм и d = 80 мм. Дифференциальный манометр водомера заполнен ртутью и водой. Определить расход воды Q при показании манометра h=200 мм. Коэффициент расхода, учитывающий потери энергии в водомере, = 0,98.
Рисунок 4.1. К задаче 4.2.2
Решение. Расход определится по формуле
Q=(D2/4)·(1/(2·(D4/d4)-1))1/2·2gh(рт-)/1/2=0,0344 м3/с
Задача 4.2.3. Вода в количестве Q = 30 л/с подается в эжектор с помощью центробежного насоса, создающего в подводящей трубе Т давление р1 = 2 атм. Размеры эжектора следующие: D = 100 мм и d = 50 мм. Вода из напорной линии К установки должна изливаться в атмосферу. Можно ли данным эжектором поднять воду из резервуара, расположенного на Н = 4,5 м ниже оси эжектора?
Рисунок 4.2. К задаче 4.2.3
Решение. По следующей зависимости определим вакуум, который создается в эжекторе при заданных его размерах:
hВАК=(16Q2/22g)·((1/d4) – (2 / D4)) + (pam / ) – (p1 / ) = 1,84 м.
Так как образующийся вакуум меньше высоты подъема Н=4,5 м, то эжектор воду из резервуара засосать не сможет.
Следовательно, требуется увеличение расхода рабочей жидкости или снижение давления в подводящей трубе.
Задача 4.2.4 Сифон длиной l = l' + l' = 25 м и диаметром d = 0,4 м (рисунок 4.3) позволяет перетекать воде из одного резервуара в другой. Центральная часть сифона поднимается на высоту h1=2 м над свободной поверхностью жидкости. Разница уровней в резервуарах z = 2,5 м. Коэффициент потери напора по длине λ = 0,02, коэффициенты местных потерь: входа ξ1 == 0,5, выхода ξ2 = 1, поворота трубопровода ξ3 = 0,4. Определить расход воды в сифоне.
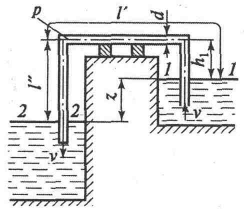
Рисунок 4.3. К задаче 45.2.4
Решение. Сечения 1 - 1 и 2 - 2 проведем через свободные поверхности резервуаров, а плоскость сравнения - через сечение 2 - 2.
Используем уравнение Бернулли для сечений 1 - 1 и 2 - 2
.
Здесь
;
р1 = р2 = ратм;
α1 = α2 = 1 (предположим, что режим течения турбулентный)
Тогда
;
;
z1
- z2
=2,5
м
Отсюда
м/с;
м3/с.
4.3 Задачи для самостоятельного решения
Задача 4.3.1 Расходомер Вентури расположен в наклонном трубопроводе с диаметрами d1 = 0,25 м и d2 = 0,1 м (рисунок 4.4). В двух сечениях ртутным манометром производится замер разности давлений. Зная разницу давлений h = 0,1 м ртутного столба, определить расход воды (ρрт = 13600 кг/м3).
Задача 4.3.2 Идеальная жидкость относительной плотностью δ = 0,8 перетекает через систему трех трубопроводов с диаметрами d1 = 50 мм, d2 = 70 мм, d3 = 40 мм под постоянным напором Н =16 м (рисунок 4.5). Трубопроводы полностью заполнены жидкостью. Определить расход жидкости Q.
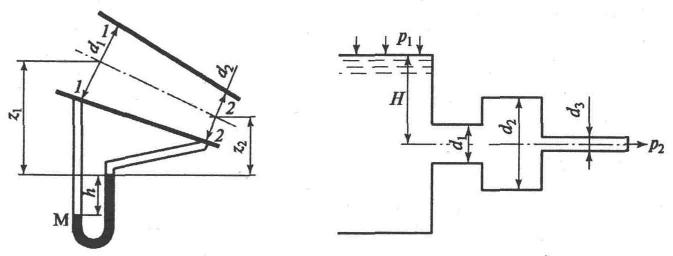
Рисунок 4.4. К задаче 4.3.1 Рисунок 4.5. К задаче 4.3.2
Задача 4.3.3. Пренебрегая всеми потерями напора, определить высоту Н и расход Q струи воды (ρв = 1000 кг/м3) начальным диаметром d = 25 м при выходе из сопла длиной h = 0,25 м. Выброс струи осуществляется вертикальной трубкой диаметром D = 500 мм и длиной Н0 = 3 м, которая подпитывается из резервуара с постоянным уровнем под избыточным давлением рм = 5 Н/см2 = 5·104 Н/м2 над свободной поверхностью (рисунок 4.6).
Задача 4.3.4. Центробежный насос должен обеспечить расход Q = 0,1 м3/с и давление на выходе р2 = 4,7·104 Н/м2. Всасывающая труба имеет диаметр d = 0,3 м и длину b = 24 м, а также фильтр на входе, имеющий местный коэффициент сопротивления ξ = 5. Всасывание воды осуществляется из открытого резервуара (рисунок 4.7). Коэффициент потерь на трение λ = 0,02, коэффициент местных сопротивлений ξповорот = 0,2. Определить высоту всасывания Нвс.
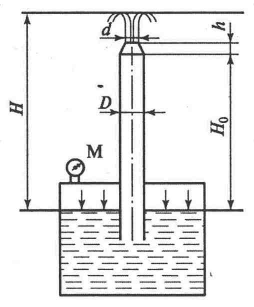
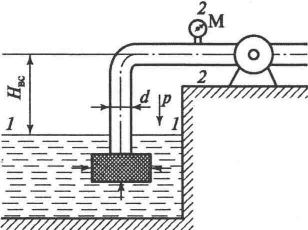
Рисунок 4.6. К задаче 4.3.3 Рисунок 4.7. К задаче 4.3.4