2.3 Задачи для самостоятельного решения

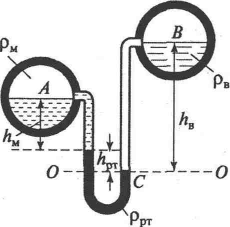
Задача 2.3.1. Два горизонтальных цилиндрических трубопровода А и В (рисунок 2.4) содержат соответственно минеральное масло плотностью 900 кг/м³ и воду плотностью 1000 кг/м³. Высоты жидкостей, представленные на рисунке 2.4, имеют следующие значения: h_м = 0,2 м; h_рт = 0,4 м; h_в ⁼ 0,9 м. Зная, что гидростатическое давление на оси в трубопроводе А равно 0,6·10⁵ Па, определить давление на оси трубопровода В.

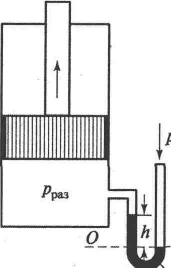
Задача 2.3.2. К всасывающей стороне цилиндра присоединен водяной вакуумметр с показанием h = 0,42 м. Определить разрежение под поршнем (рисунок 2.5).

Рисунок 2.4. К задаче 2.3.1	Рисунок 2.5. К задаче 2.3.2

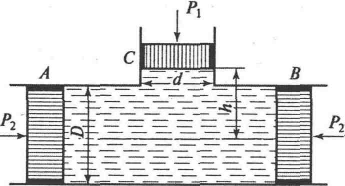
Задача 2.3.3. Какая сила должна быть приложена к поршням А и В для уравновешивания системы поршней А, В, С (рисунок 2.6), если h = 80 см; D = 40 см; d = 5 см; Р₁ = 72,64 Н; ρ = 10³ кг/м³; g = 10 м/с²?

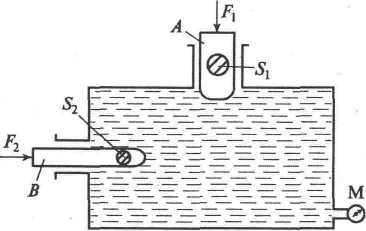
Задача 2.3.4 Два плунжера А и В, расположенные в горизонтальной плоскости, уравновешены (рисунок 2.7). Определить показания манометра и силу F₂, если сила F₁ = 600 Н, площади плунжеров соответственно S₁ = 60 см², S₂ = 5 см².

Рисунок 2.6. К задаче 2.3.3	Рисунок 2.7. К задаче 2.3.4

2.4 Вопросы для самопроверки

1 Сформулируйте и объясните свойства давления в точке покоящейся жидкости.

2 Запишите уравнение равновесия жидкости (уравнение Л. Эйлера) в двух формах и объясните входящие в него величины.

3 Что такое поверхность равного давления и свободная поверхность жидкости? Какую форму они имеют в случае, когда жидкость находится в равновесии в поле действия силы тяжести?

4 Запишите основное уравнение гидростатики и объясните входящие в него величины.

5 Дайте определения манометрического давления и вакуума и укажите, в каких пределах они могут изменяться. Поясните это графически.

6. Сформулируйте закон Паскаля и приведите примеры его применения.

7 Как определить силу давления жидкости и ее составляющие на криволинейную стенку? Какие величины входят в расчетные формулы для определения этих сил?

Практическое занятие № 3. Гидростатика. Закон паскаля. Силы давления жидкости на криволинейные поверхности.

3.1 Теоретические положения

Это занятие является продолжением практического занятия № 2, поэтому теоретические положения, необходимые для решения задач, изложены ранее.

3.2 Задачи с решениями

Задача 3.2.1. При отливке бандажа для колеса с целью придания стали большей плотности форма, в которой отливается бандаж, приводится во вращение. Определить избыточное давление в точке А в неподвижной и вращающейся формах. Число оборотов формы n= 120 об/мин, D = 1850 мм, h = 300 мм, объемный вес расплавленной бандажной стали _{с т} = 7800 кг/м³.

Рисунок 3.1. К задаче 3.2.	Рисунок 3.2. К задаче 3.2.2

Решение. Избыточное давление в неподвижной форме

р₁ = _стh = 7800·0,3 = 2340 кг/м² = 0,234 кг/см².

Избыточное давление при вращении, согласно зависимостям, будет больше на величину

p = _ст(² r² / 2g) = _ст(u² / 2g).

Следовательно, искомое избыточное давление при вращении формы равно

p₂ = p₁ + _ст(Dn / 60)² = 2340 + 53 700 = 56050 кг/м² = 5,6 кг/см².

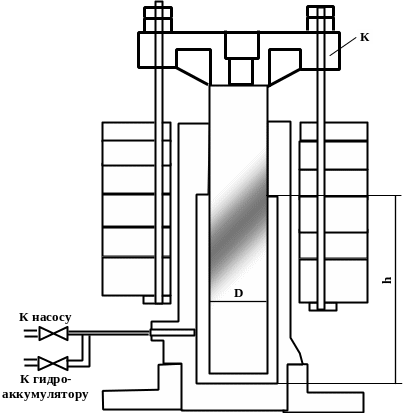
Задача 3.2.2. Определить силу осевого давления P₀ на верхний обод рабочего колеса гидравлической турбины, если гидродинамическое давление у периферии рабочего колеса равно р = 6 атм. Диаметр колеса турбины D = 2000 мм, число оборотов n = 300 об/мин.

Решение. Искомая сила осевого давления Р₀ будет равна вертикальной составляющей силы давления жидкости на колесо турбины.

Указанная вертикальная составляющая равна

Р_ = ·V,

где V - объем жидкости.

В рассматриваемом случае объем жидкого тела равен объему цилиндра диаметром D и высотой Р/ = 60 м, сложенному с объемом параболоида вращения высотой h = (²r² /2g), согласно зависимости. Тогда сила осевого давления Р₀

Р₀=Р_z=(D²/4)·(p/+h/2)=(D²/4)·(p/+²r²/4g)=

=(D²/4)·p/+1/4g·(nD²·60),

так как =2n/60 и r=D/2, если предположить, что угловая скорость вращения со колеса и воды одинакова. Следовательно,

P₀=((1·3,14·2²)/4)·60+(1/4·9,81)·((3,14·360·2)/60)² =267 атм.

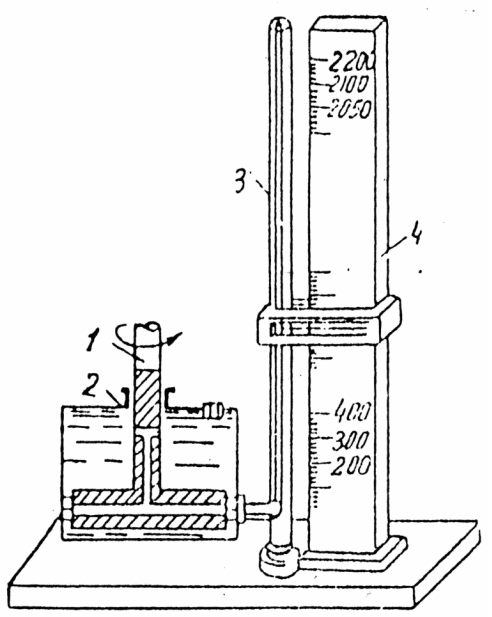
Задача 3.2.3. Выше отмечалось, что для измерения числа оборотов вала могут быть использованы жидкостные тахометры, принцип работы которых основан на теории относительного покоя жидкости.

Схема гидравлического тахометра состоит из вала 1, воспринимающего скорость вращения вала машины, с насаженным на него диском, имеющим радиальные и осевые каналы. Диск помещен в герметически закрытую камеру 2, заполненную машинным маслом. Камера соединена с пьезометром 3, расположенным на шкале 4. Посредством пьезометра можно измерять давления, возникающие в камере 2 при вращении диска. Шкала пьезометра наносится опытным путем. При вращении диска в жидкости развиваются центробежные силы, а в камере увеличивается давление, что отражается на показаниях пьезометра.

Рисунок 3.3. К задаче 3.2.3	Рисунок 3.4. К задаче 3.2.4

Предположим, что в результате вращения диска пьезометр показал отсчет Н = 0,85 м. Определим число оборотов вала, если радиус диска тахометра равен 0,20 м, а показания пьезометра при остановке тахометра h = 0,35 м.

Решение. Пользуясь формулой, определим давление, которое будет возникать в камере у наружной поверхности диска:

p = (²R² / 2) + h.

С другой стороны, это давление должно быть равно

p = Н,

где H - высота столба жидкости в пьезометрической трубке 3.

Тогда

H = ·(²R² / 2g) + h,

или

H - h = ²R² / 2g.

Заменяя  = 2n / 60 = n / 30, окончательно получаем

n = 30 / R·2g·(H - h)  ^0,5 (71)

Подставляя в найденную зависимость заданные числовые значения, определим число оборотов вала:

n = 149,5 об/мин.

Задача 3.2.4. Определить, какое усилие Q должно быть приложено к рукоятке поршневого насоса, чтобы гидравлический пресс сжимал тело G с силой Р = 3000 кГ. Диаметр поршня насоса d = 5 см, диаметр плунжера пресса D = 30 см, вес тела G и плунжера - 200 кГ. Длина рукоятки насоса а = 25 см, длина плеча b = 5 см. На трение в манжетах пресса теряется 5 % усилия, возникающего под плунжером пресса.

Решение. Определим сначала ту силу, которую необходимо приложить к плунжеру пресса:

P₂ = (P + G) / 0,95 = 3368 кГ.

Среднее давление под плунжером пресса должно быть равно

p = P₂ / (D² / 4),

а сила, приложенная к поршню насоса:

P₁ = p·(d² / 4) = (P₂ / (D² / 4))·(d² / 4) = P₂·(d / D)².

Поэтому искомое усилие Q составляет

Q = (b / a)·P₁ = (b / a)·(d / D)²·P₂ = 18,7 кГ.

Задача 3.2.5. Определить диаметр цилиндра D плунжера гидравлического аккумулятора, приводящего в движение гидравлический подъемник, который работает под давлением 3 атм и должен поднимать груз G = 2000 кГ на высоту h = 1,5 м. Высота хода плунжера аккумулятора h = 1,5 м, КПД подъемника _п = 0,45, КПД аккумулятора _А = 0,80.

Рисунок 3.5. К задаче 3.2.5	Рисунок 3.6. К задаче 3.2.6

Решение. Коэффициент полезного действия системы равен отношению произведенной полезной работы GН к энергии, израсходованной аккумулятором рW, где W - рабочий объем гидравлического цилиндра аккумулятора:

 _с = (GH) / (pW) = _А·_п.

Следовательно, рабочий объем аккумулятора должен быть равен

W = (D² / 4)·h = (GH) / (p _A·_п),

и соответственно диаметр плунжера

D = (4W) / ( h) ^1/2 = (4GH) / ( p _A·_п h) ^1/2 = 0,687 м.

Задача 3.2.6. Горизонтальная металлическая цистерна круглого сечения диаметром D = 2,6 м, длиною ℓ = 9,6 м полностью заполнена нефтью с объемным весом _нефт = 900 кг/м³. Давление на поверхности нефти равно атмосферному. Требуется определить силу давления нефти на половину внутренней криволинейной поверхности цистерны adc, а также силу суммарного давления жидкости на эту поверхность.

Решение. На половину внутренней поверхности цистерны действует горизонтальная составляющая силы суммарного давления, равная, согласно зависимости:

P_х =  _· _нефт h_C = ℓ D _нефт·(D / 2) = l _нефт (D² / 2) =

= 9,6·900·2,6² / 2 = 29200 кГ = 29,2 т.

Для определения суммарной силы давления жидкости необходимо предварительно установить ее вертикальную составляющую Р_z по уравнению:

P_z = W_тд = _нефт·(l  D² / 8) = 22900 кГ = 22,9 т.

Тогда сила суммарного давления нефти, действующего на половину внутренней поверхности цистерны, может быть найдена по уравнению:

P =(P²_Z + P²_X)^1/2 = 37,11 т.

Задача 3.2.7. Прямолинейный понтон весом G = 4000 кГ имеет следующие размеры: длина равна 8,0 м, ширина С = 4,0 м, высота Н=1,0 м. Центр тяжести понтона расположен на высоте h₁=0,45 м от дна понтона. Определить предельную грузоподъемность понтона G₂ при высоте бортов над уровнем воды 0,20 м, а также метацентрический радиус , обеспечивающий остойчивость понтона.

Рисунок 3.7. К задаче 3.2.7

Решение. Предельная грузоподъемность понтона равна разности между весом вытесненного погруженной частью понтона объема воды и весом понтона: G₂ = Н₁LB - G₁ = 21,6 т.

Понтон с грузом G₂ будет остойчив, если метацентрический радиус  больше расстояния е между центром тяжести А понтона с грузом и центром водоизмещения:

 - е  0.

Предположим, что в результате выполненных расчетов для предельной грузоподъемности в 21,6 т расстояние между центром тяжести груженого понтона и центром его водоизмещения е = 1,05 м. Примем для запаса, что  = 1,3 е. Тогда

 = l / W = LC³ / (12 LCH₁) = C² / 12 H₁ = 1,67 м.

По принятому выше условию метацентрический радиус должен быть равен

 = 1,3 е = 1,3·1,05 = 1,365 м.

Так как 1,67  1,365, остойчивость понтона обеспечена.

Задача 3.2.8. Регулирование подачи бензина в карбюратор мотора автомобиля производится с помощью поплавка, соединительного с рычагом, укреплённым в шарнире. При переполнении поплавковой камеры горючим поплавок поворачивает рычаг, благодаря чему игла перекрывает доступ горючего. Определить диаметр поплавка, исходя из условия, что в камере поддерживается постоянный уровень бензина и поплавок в момент прекращения доступа бензина погружен наполовину. При этом а = 50 мм; b = 15 мм; d = 5 мм; вес поплавка G = 20 г; вес иглы Q = 10 г, _б = 700 кг/м³, избыточное давление бензина на иглу р = 0,4 атм. Весом рычага можно пренебречь.

Рисунок 3.8. К задаче 3.2.8

Решение. Обозначив поддерживающую силу поплавка через Р_П и силу давления бензина на иглу через Р, составим уравнение равновесия относительно шарнира рычага:

(Р_П - G)a - (Q + P)b = 0

Отсюда

P_П= (Q + P)·(b / a) = G ;

P = pd² / 4 = 0,785 кг = 785 г.

Р_П = 258,5 г.

С другой стороны, подъемная сила Р_П, может быть определена по зависимости

Р_П = ( D³ / 12)· _б

Отсюда

D = ((12 Р_П) / ( _б))^1/3 = 5,2 см.