10. Иерархическая модель данных
Иерархическая модель данных основана на принципе иерархического подчинения типов объектов. Среди объектов предметной области выделяют порождающие типы объектов и порожденные типы. Между ними устанавливаются допустимые в иерархии связи.
Иерархическая модель данных – частный случай сетевой модели, так как дерево представляет собой граф, на который наложены определенные ограничения. Так, например, в дереве возможны только однонаправленные связи - от порождающей вершины к порожденной. Каждая порожденная вершина может иметь единственную порождающую вершину, но каждая порождающая – любое количество порожденных вершин. Поэтому в иерархической модели могут присутствовать лишь связи 1:М.
Сеть приводится к виду дерева введением избыточности. При этом все вершины сети неоднократно повторяются в тех деревьях, которыми заменяют сеть.
Полученная выше сетевая модель данных представляет собой сложную сеть, т.к. она имеет вид ориентированного мультиграфа (между объектами, входящими в сеть, имеются двусторонние связи). К виду дерева можно привести лишь простую сеть, представленную графом, не имеющим параллельных ребер. Если в виде дерева надо представить сложную сеть, то последнюю вначале приводят к простому виду, а потом полученные простые сети заменяют деревьями.
Преобразуем сложную сеть к виду простой сети, а затем к виду дерева.
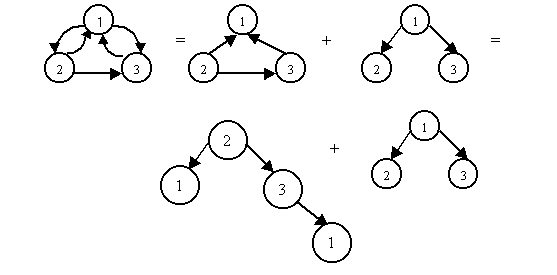
На рисунке цифрой 1 обозначена вершина, содержащая запись об объекте ПРЕПОДАВАТЕЛЬ, цифрой 2 – вершина СТУДЕНТ, цифрой 3 – вершина ПРЕДМЕТ. Из рисунка видно, что иерархическая модель данных рассматриваемой предметной области состоит из двух типов деревьев, причем отдельные вершины деревьев повторяются неоднократно.
Р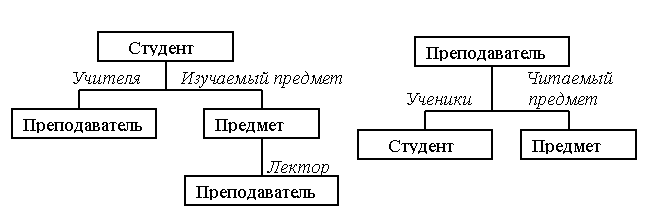
азместив
в вершинах экземпляры записей, т.е.
определив значения полей, изобразим
фрагмент экземпляра схемы. На рисунке
изображены два экземпляра дерева первого
типа.
В БД будет содержаться множество экземпляров деревьев каждого типа: количество экземпляров деревьев первого типа равно числу студентов, количество экземпляров деревьев второго типа равно числу преподавателей. Текущее состояние БД – это совокупность всех экземпляров деревьев каждого типа.
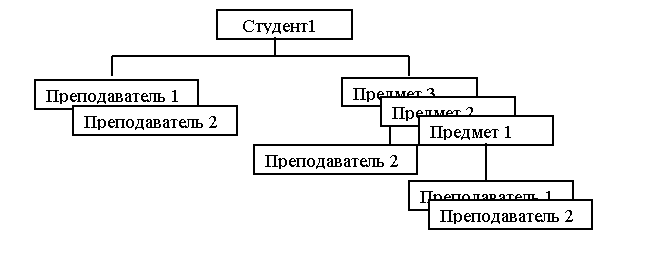
И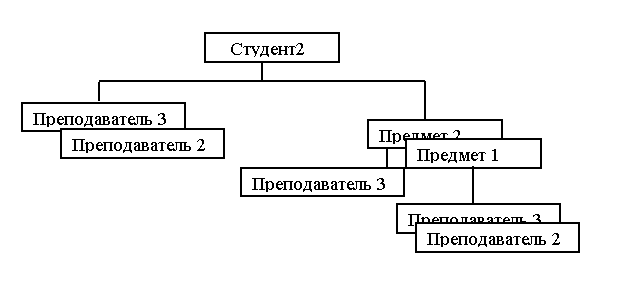
ерархическая
модель данных обладает избыточностью.
Экземпляры записей неоднократно
повторяются в экземплярах деревьев.
Реляционная модель данных
Реляционная модель была предложена американским математиком Е. Коддом в 1970 г. Это единственная из моделей БД, основанная на специальном разделе математики - теории отношений. Благодаря математическому обоснованию удалось сформулировать достаточно строгие правила построения модели данных. Языки данных, основанные на математическом аппарате теории отношений, позволяют составлять любые запросы к БД и выполнять разнообразные операции манипулирования данными.
В реляционной модели все данные представлены в табличной форме. Каждому типу объекта сопоставлена отдельная таблица. Таблице присваивается имя, обычно совпадающее с именем объекта. Свойствам объекта сопоставлены столбцы таблицы, называемые также полями. Каждое поле имеет уникальное имя, обычно совпадающее с именем соответствующего свойства. Строки каждой таблицы, называемые также записями, содержат значения свойств и соответствуют экземплярам объекта данного типа.
Представим объекты рассматриваемой предметной области в табличной форме.
СТУДЕНТ ПРЕПОДАВАТЕЛЬ
№ зач. кн. |
ФИО |
Группа |
Ср. балл |
|
ФИО_П |
Должность |
213456 |
Кошкин К.К. |
х37 |
4.3 |
Лосев Л.Л. |
Доцент |
|
214365 |
Мышкин М.М. |
х38 |
3.9 |
Волков В.В. |
Профессор |
|
235467 |
Шишкин Н.Н. |
х38 |
4.8 |
Львов Л.Л. |
Доцент |
|
324476 |
Попов П.П. |
х37 |
4.5 |
|
|
ПРЕДМЕТ
Наименование
Часы
Отчетность
Математика
64
Экзамен
Физика
51
Экзамен
Физкультура
34
Зачет
Между таблицами реляционной модели должны быть установлены связи, существующие между объектами в предметной области, т.е. все те связи, которые были установлены нами в рассмотренной выше сетевой модели.
При построении реляционной модели примем следующее ограничение: каждый предмет читается определенным преподавателем. Тогда, в отличие от построенной ранее логической структуры данных, связь между объектами ПРЕПОДАВАТЕЛЬ – ПРЕДМЕТ будем рассматривать как одностороннюю – от объекта ПРЕПОДАВАТЕЛЬ к объекту ПРЕДМЕТ.
М
ПРЕПОДАВАТЕЛЬ ПРЕДМЕТ
Эта связь имеет имя Читаемый предмет.
В реляционной модели нет специальных средств для представления связей. Все связи устанавливаются через одинаковые значения одноименных столбцов, содержащихся в различных таблицах. Эти столбцы должны соответствовать одному и тому же свойству.
Для установления связи 1:М в таблицу, находящуюся на стороне М, вводятся дополнительные столбцы из таблицы, находящейся на стороне 1.Для установления связи М:М приходится создавать дополнительную связующую таблицу, содержащую столбцы из связываемых таблиц. Между каждой из связываемых таблиц и вновь созданной таблицей устанавливается связь 1:М. Если между таблицами существует связь 1:1, то их можно объединить в одну таблицу.
Установим связи между таблицами.
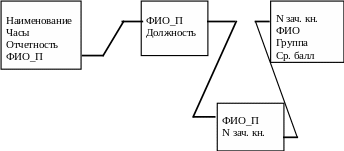
Для установления связи Читаемый предмет в таблицу ПРЕДМЕТ добавим столбец ФИО_П из таблицы ПРЕПОДАВАТЕЛЬ. Фамилия каждого из преподавателей, читающего несколько предметов, будет встречаться в таблице ПРЕДМЕТ несколько раз (по числу читаемых им предметов). Таким образом между таблицей ПРЕПОДАВАТЕЛЬ и таблицей ПРЕДМЕТ устанавливается связь 1:М.
Между таблицами СТУДЕНТ и ПРЕПОДАВАТЕЛЬ необходимо установить связь М:М (это связи Учителя и Ученики). Для этого создадим связующую таблицу СТУДЕНТ_ПРЕПОДАВАТЕЛЬ, состоящую из столбцов ФИО_П и N зачетной книжки. Эта таблица связывается с таблицей СТУДЕНТ по столбцу N зачетной книжки, а с таблицей ПРЕПОДАВАТЕЛЬ – по столбцу ФИО_П.
ПРЕДМЕТ ПРЕПОДАВАТЕЛЬ СТУДЕНТ
1 1
1
М
СТУДЕНТ_ПРЕПОДАВАТЕЛЬ
М
М
Для данной схемы связь Изучаемый предмет будет установлена между таблицами СТУДЕНТ и ПРЕДМЕТ через таблицы СТУДЕНТ_ПРЕПОДАВАТЕЛЬ и ПРЕПОДАВАТЕЛЬ.
Связующие таблицы можно рассматривать как самостоятельные объекты предметной области.
Связи, существующие между объектами предметной области, могут обладать определенными свойствами. Эти свойства можно представить дополнительными столбцами в связующих таблицах.
В процессе установления связей в таблицы вводятся избыточные данные, т.к. в связующих таблицах присутствуют столбцы, уже имеющиеся в других таблицах. Избыточность данных, присущая реляционной модели, требует особого внимания к вопросу обеспечения целостности и непротиворечивости данных.
Таблицы реляционной модели строятся по определенным правилам. Некоторые из них таковы:
- в таблице не должно быть столбцов с одинаковыми именами;
- в каждом столбце должны содержаться данные, имеющие одинаковый смысл и принадлежащие к одному и тому же типу;
- в таблицах не должно быть повторяющихся строк;
- каждое значение, содержащееся на пересечении строки и столбца, должно быть атомарным (логически неделимым);
- в таблице должен присутствовать столбец (или набор из нескольких столбцов), значения в котором не повторяются и уникальны для каждой из строк.
Эти и другие правила построения таблиц будут обсуждаться ниже.
При соблюдении всех правил построения таблиц каждую из них можно рассматривать как математическое отношение (relation). Тогда над таблицами можно выполнять математические операции реляционной алгебры и теории множеств. Именно эти операции положены в основу ЯМД реляционных СУБД.
Достоинством реляционной модели является ее наглядность, так как таблица – это привычная и понятная форма представления данных. Но самое важное достоинство реляционной модели – это ее математическая обоснованность. Этот факт обеспечивает возможность формулировки достаточно строгих правил построения модели и возможность выполнения любых манипуляций с данными.
Недостатком реляционной модели является избыточность данных, возникающая при установлении связей.
Теория реляционных БД
Понятие отношения
Рассмотрим некоторые основные понятия теории отношений, необходимые для дальнейшего рассмотрения реляционной модели данных.
Парой или упорядоченной парой называют два объекта, взятых в определенном порядке.
Примеры пар: <x, y>, <1, 2>, <2, 2>.
Пара отличается от двухэлементного множества следующим:
- в паре порядок элементов имеет значение;
- первой и второй компонентами пары может быть один и тот же объект, тогда как в множество каждый объект может входить только один раз.
Упорядоченная последовательность произвольной конечной длины называется кортежем. Пара представляет собой кортеж длиной 2.
Бинарным отношением, заданным на множествах M и N, является некоторое подмножество тех пар (кортежей) <x, y> из декартова (прямого) произведения M*N, между элементами которых существует связь R. Здесь R – имя отношения.
Бинарное отношение – это множество кортежей длиной 2.
Для кортежей, принадлежащих отношению R, приняты следующие обозначения:
x R y - -x находится в отношении R к y;
R(x, y) – между x и y существует отношение R;
<x, y> R – кортеж <x, y> принадлежит отношению R.
Пусть заданы два множества M = {m1, m2} и N = {n1, n2, n3}. В результате декартова произведения множеств M*N будет получено множество кортежей: {<m1, n1>, {m1, n2>, <m1, n3>, <m2, n1>, <m2, n2>, <m2, n3>}. Отношению R будут принадлежать те кортежи, для которых m i находится в отношении R к n j.
В частном случае можно задать отношение на одном множестве M. Это будет подмножество кортежей из декартова произведения M*M.
Пример
Определим отношение с именем МЕНЬШЕ на множестве целых чисел M= {1, 2, 3}. Декартово произведение M*M представляет собой множество кортежей <1,1>, <1, 2>, <1, 3>, <2, 1>, <2, 2>, <2, 3>, <3, 1>, <3, 2>, <3, 3>.
Отношению МЕНЬШЕ принадлежат те кортежи декартова произведения, у которых первый элемент меньше второго.
МЕНЬШЕ={ <1, 2>, <1, 3>, <2, 3>}.
Пример
Пусть множество M1 содержит имена детей одной семьи.
M1 = {Таня, Галя, Сережа}
Тогда отношение с именем БРАТ состоит из двух кортежей: <Сережа, Таня>, <Сережа, Галя>, а отношение СЕСТРА состоит из четырех кортежей: <Таня, Галя>, <Таня, Сережа>, <Галя, Таня>, <Галя, Сережа>.
Отношения, заданные на одном или двух множествах являются бинарными. Кортежи таких отношений содержат по два элемента.
Возможны n-местные или n-арные отношения, задаваемые более чем на двух множествах и содержащие кортежи длиной n.
Состояние реляционной БД можно описать как совокупность некоторых множеств М1, М2, ….., Мi, ….., Мn, на которых задан ряд отношений. Каждое отношение представляет собой подмножество кортежей из декартовых произведений определенных множеств. Множества, на которых задано конкретное отношение, называются несущими множествами для данного отношения.
Каждое множество образовано элементами одного типа. Это может быть, например, множество целых чисел (в нашем примере это множество М), множество имен (множество М1), множество названий городов, множество календарных дат и т.п. Следовательно, можно говорить о сортах или типах множеств. Каждый элемент каждого множества имеет имя. Это имя представляет собой константу. Поскольку множество не может содержать одинаковых элементов, то имя каждого элемента множества должно быть уникальным.