Исследование цепей с распределёнными параметрами

Цель работы: экспериментально исследовать распределение напряжения вдоль однородной длинной линии при различных сопротивлениях нагрузки.

Общие сведения

В современной радиотехнике всё более широкое применение находят устройства, геометрические размеры которых соизмеримы или больше длины волны распространяющихся в них электромагнитных колебаний. Например, рассматривая передачу электромагнитной энергии в линиях связи, фидере, волноводе, антенне и т.п., следует учитывать, что магнитные и электрические поля распределены по всей длине этих устройств, и превращение электромагнитной энергии в тепло также происходит по всей длине устройств. Такие цепи характеризуются распределёнными по всей длине индуктивностями, ёмкостями, активными сопротивлениями и называются цепями с распределёнными параметрами. Воздействие генератора на такую цепь проявляется в некоторой точке цепи не мгновенно, а с запаздыванием на время, определяемое длиной пути тока между генератором и этой точкой и скоростью распространения колебаний в цепи. Поэтому мгновенное значение тока в реальной цепи с конечными размерами принципиально не может быть везде одинаково.

Простейшими цепями с распределёнными параметрами являются длинные линии (двухпроводные воздушные линии связи, симметричные и коаксиальные кабельные линии проводных систем связи, полосковые линии передачи и т.п., имеющие длину l ,

- длина волны электромагнитных колебаний).

Линии передачи, геометрическая конфигурация, а также свойства материалов (проводников и диэлектриков), которых остаются неизменными по всей длине, называются однородными, или регулярными.

Рассмотрим в качестве примера двухпроводную линию передачи с известным сопротивлением нагрузки на конце (рис.1).

Электромагнитные свойства такой линии характеризуются первичными параметрами, т.е. параметрами, отнесёнными к единице длины линии:

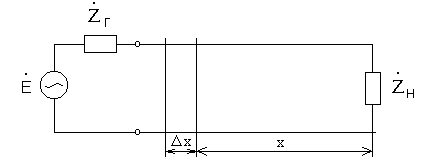
Рис.1

Строгое решение задачи о зависимости тока в линии от времени и координаты х может быть получено из системы уравнений Максвелла. Однако этот метод имеет существенный недостаток, заключающийся в том, что решение системы уравнений Максвелла удаётся довести до конца только для ограниченного класса линий передачи с достаточно простой конфигурацией.

Если же представить длинную линию в виде отрезков длиной X каждый, то в пределе при X0 такие малые элементы линии могут быть описаны методами, принятыми в теории цепей. В этом случае любой малый отрезок линии можно представить в виде эквивалентной схемы (рис.2), состоящей из сосредоточенных малых элементов L=L₁X, C=C₁X, R= R₁X, g= g₁X.

Рис.2 Рис.3

Вся же линия может быть представлена каскадным соединением элементарных четырёхполюсников (рис.3), где Z₁= R₁+jL₁ - погонное комплексное сопротивление, Y₁= g₁+jC₁ - погонная комплексная проводимость.

Обозначив символами комплексные амплитуды напряжений и токов соответственно на входе и выходе элементарного четырёхполюсника для внутреннего контура и узла А на основании второго и первого законов Кирхгофа, получим тождества

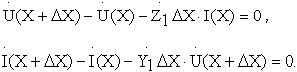
С точностью до малых величин второго порядка

Представим последние тождества системой разностных уравнений:

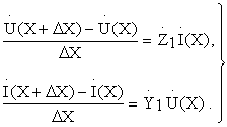
Совершая предельный переход при , получим систему двух дифференциальных уравнений с постоянными коэффициентами, которые называются телеграфными уравнениями

Если продифференцировать обе части телеграфных уравнений по х, то последняя система может быть сведена к двум дифференциальным уравнения второго порядка как относительно напряжения, так и относительно тока:

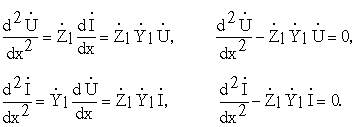
В теории волновых процессов эти уравнения носят название уравнений Гельмгольца, их общее решение записывается следующим образом:

где - комплексный коэффициент распространения.

Первые слагаемые в выражениях для напряжения и тока определяют комплексные амплитуды падающих волн, а вторые - отраженных волн напряжения и тока.

Постоянные интегрирования определяются из начальных условий:

где - волновое сопротивление линии.

Подставив постоянные интегрирования в уравнения для и , получим

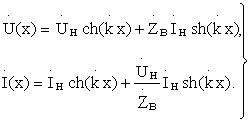
Для линии без потерь R₁=g₁=0, , где  - фазовая постоянная, показывающая отставание фазы колебаний за время их распространения на единице длины.

В зависимости от соотношения сопротивления нагрузки и волнового сопротивления линия работает в режиме бегущих волн, стоячих или смешанных волн.