Гармонические колебания

Механические гармонические колебания

Физическим маятником называется абсолютно твердое тело, совершающее колебание под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести.

Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебания под действием силы тяжести.

Н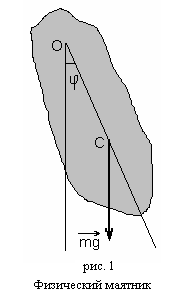 а рисунке 1 показано сечение физического маятника плоскостью, перпендикулярной к оси вращения и не проходящей через центр масс . Расстояние равно . При отклонении маятника от

положения равновесия на угол под действием силы тяжести возникает вращательный момент сил , стремящейся вернуть маятник в положение равновесия. Величина момента сил

равна ,

где – масса маятника. При малом угле

(1)

Для вывода закона движения маятника используем основной закон динамики вращательного движения:

(2)

где – момент инерции маятника относительно оси , – угловое ускорение. Спроектировав (2) на положительное направление оси вращения, связанное правилом буравчика с вектором , и подставляя (1) в (2), получим:

.

Поделив на , получим :

Введем обозначение:

(3)

– циклическая частота колебаний; тогда придем к стандартному дифференциальному уравнению гармонических колебаний:

(4)

Его решением является периодическая функция с периодом , которая имеет вид:

(5)

Где – амплитуда колебаний, – начальная фаза колебаний, – фаза колебаний.

Следовательно, при малых углах отклонения маятника угловое отклонение изменяется со временем по гармоническому закону.

Амплитуда – это максимальное значение колеблющейся величины.

Период – время одного полного колебания.

Частота – число колебаний за единицу времени.

Период колебаний физического маятника

(6)

Для математического маятника формулу циклической частоты и периода можно получить из (3) и (6), если рассматривать математический маятник как частный случай физического, у которого вся масса сосредоточена в центре масс на расстоянии от подвеса. Тогда из (6):

(7)

Из сопоставления формул (6) и (7) получается, что математический маятник с длиной будет иметь такой период колебаний, как и данный физический маятник. Величину называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Сложение взаимно-перпендикулярных колебаний

Заставим материальную точку участвовать в двух взаимно-перпендикулярных колебаниях по осям и , тогда она будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит как от соотношения частот так и от разности фаз обоих колебаний.

Пусть частоты обоих колебаний одинаковы, а уравнения их представим так:

(8)

где и – амплитуды колебаний соответственно вдоль и .

– их разность фаз .

Система представляет собой по сути дела уравнение искомой траектории в параметрической форме. Чтобы получить уравнение траектории в явном виде, исключим параметр из системы. Для этого разделим каждое уравнение системы на соответствующую ему амплитуду и получим:

Используя тригонометрическое тождество:

,

получим

.

Затем подставляя

,

получим

.

Последнее уравнение возводя в квадрат приводим к виду:

(9)

Из аналитической геометрии следует, что это уравнение эллипса с произвольно ориентированными осями, вписанного в прямоугольник со сторонами и , ограничивающего пространство, в котором совершаются колебания (рис. 2). Ориентация относительно осей зависит от разности фаз .

Рассмотрим случай , где В этом случае система уравнений (8) с помощью формулы приведения преобразуется к виду:

(10)

Поделим одно уравнение на другое и выразим :

(11)

Это значит, что точка движется по прямой. При или точка совершает гармоническое колебание с частотой и

а мплитудой вдоль прямой (рис. 3).

При или точка совершает колебания вдоль прямой (рис. 4.).

Если , то используя формулу приведения система уравнений приведем к виду:

(12)

Выразим уз уравнений и , возведем каждое уравнение в квадрат и, сложив их, получим:

(13)

То есть точка движется по эллипсу (рис. 5), оси которого совпадают с осями координат, а полуоси равны и . П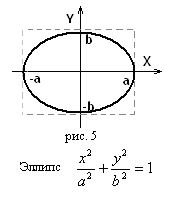 ри этом, если , то точка движется по часовой стрелке, если , то против часовой стрелки.

Если частоты взаимно-перпендикулярных колебаний отличаются на малую величину , то можно считать, что они происходят с одинаковой частотой, а разность фаз медленно меняется: . В этом случае траектория будет медленно меняться, последовательно проходя все этапы, показанные на рис. 2 – 5.

Р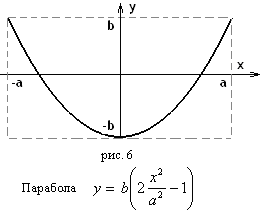 ассмотрим случай, когда частоты складываемых колебаний отличаются в два раза, например , .

Тогда система уравнений (8) примет вид:

Используя формулу косинуса двойного угла, получим уравнение параболы:

(14)

Уравнение траектории – парабола (рис. 6)

В случае, когда частоты взаимно-перпендикулярных колебаний неодинаковы и кратны: , траектория результирующего движения имеют вид довольно сложных кривых, называемых фигурами Лиссажу, вписанных в прямоугольник , ограничивающий колебания по осям X и Y. При этом количество точек касания фигуры Лиссажу по горизонтали равно , а по вертикали – .

СТРОЙСТВО И ПРИНЦИП ДЕЙСТВИЯ

ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА

Электронный осциллограф используют для исследования быстропеременных периодических процессов. Например, с помощью осциллографа можно измерить силу тока и напряжение, рассмотреть их изменение во времени. Можно измерять и сравнивать частоты и амплитуды различных переменных напряжений. Кроме того, осциллограф при применении соответствующих преобразователей позволяет исследовать неэлектрические процессы, например, измерять малые промежутки времени, периоды колебаний и т. д. Достоинствами электроннолучевого осциллографа является его высокая чувствительность и безынерционность действия, что позволяет исследовать процессы, длительность которых порядка 10^-6 – 10^-8 с.

Основным элементом электронного осциллографа является электроннолучевая трубка. Схематическое устройство такой трубки показано на рис. 7.

Электроннолучевая трубка состоит из подогревного катода (2) и нити накала (1). За катодом расположен управляющий электрод (3) в виде сетки или цилиндра с отверстиями. Работа его аналогична работе управляющей сетки в электронной лампе. При изменении потенциала управляющего электрода относительно катода изменяется интенсивность электронного потока, тем самым проводится изменение яркости светового пятна на экране трубки.

Первый и второй аноды (4 и 5), в виде цилиндров с диафрагмами, обеспечивают необходимую скорость движения электронов и создают электрическое поле определенной конфигурации, фокусирующее электронный поток в узкий пучок (луч).

Затем сфокусированный электронный луч проходит между двумя парами взаимно перпендикулярных отклоняющих пластин. При разных потенциалах на одной из пар отклоняющих пластин луч отклоняется в сторону пластины с большим потенциалом, причем отклонение луча пропорционально величине приложенного напряжения. Вертикальные пластины (7) обеспечивают горизонтальное перемещение электронного луча по экрану, а горизонтальные (6) дают вертикальное перемещение луча. Электроннолучевая трубка заключена в стеклянный баллон, из которого выкачан воздух до давления порядка 10^-6 мм рт. ст., и на передней части которого нанесен тонкий слой флуоресцирующего вещества. Под воздействием электронного луча экран начинает светиться.

Кроме генератора напряжения развертки и электроннолучевой трубки в осциллографе имеются два усилителя. Один из них, предназначенный для усиления исследуемого напряжения, обычно называют вертикальным усилителем, так как напряжение с него подается на горизонтально расположенные пластины электроннолучевой трубки, которые обеспечивали вертикальное отклонение луча по экрану. Напряжение от второго усилителя подается на вертикальные пластины, обеспечивающие горизонтальное перемещение луча. Этот усилитель называется горизонтальным. Напряжение генератора развертки подается на пластины через горизонтальный усилитель.

Для исследования характера изменения электрических сигналов во времени используют специально вмонтированное в осциллограф устройство, называемое генератором развертки. Этот генератор вырабатывает пилообразное напряжение (рис. 8), которое за время линейно нарастает от нуля до максимального значения , а затем за очень малое время падает до нуля. Частоту пилообразного напряжения можно изменять с помощью рукоятки «частота развертки». Пилообразное напряжение подается обычно на вертикальные пластины. При этом луч откланяется по горизонтали на величину пропорциональную значению пилообразного напряжения в данный момент. Так как это напряжение линейно возрастает со временем, то по горизонтали луч движется равномерно, что соответствует ходу времени, и, значит, смещение луча по горизонтали пропорционально времени. Поэтому при включенном генераторе развертки горизонталь считают осью времени. При малых частотах развертки можно увидеть поступательное равномерное движение точки по горизонтали. Если частота развертки большая, то на экране видна только горизонтальная линия. Это происходит в силу инерции зрительного восприятия и послесвечения трубки. т. е. зрительно при больших частотах мы не успеваем отметить последовательное перемещение луча по экрану слева направо при увеличении напряжения_. от нуля до максимума и почти мгновенное возвращения луча в исходное положение. На каждом следующем «зубце пилы» луч движется по одному и тому же следу слева направо по горизонтали и обратно, и повторяется это с частотой равной частоте развертки.

Чтобы увидеть, как меняется со временим исследуемое напряжение, надо одновременно подать на – вход напряжение развертки, а на – вход исследуемый сигнал . Пусть к моменту времени исследуемый сигнал достигает значения , а напряжение развертки значения . Луч, участвуя одновременно в двух взаимно перпендикулярных движениях: по горизонтали (под действием напряжения развертки) и по вертикали (под действием исследуемого напряжения ), переместится в точку (рис. 8). Если исследуемое напряжение меняется по гармоническому закону и его период совпадает с периодом развертки , то в течение времени на экране луч «выпишет» один период синусоиды. На каждом следующем зубце пилы при достижении напряжением значений и т. д. электронный луч будет попадать соответственно в те же точки и т. д. синусоиды, что и на первом зубце. Вообще, изображение на экране осциллографа будет неподвижным, если период развертки равен или в целое число раз больше периода исследуемого сигнала. При невыполнении этого условия (часто случающегося из–за нестабильности частоты генератора развертки) изображение будет «плыть» по экрану.

Для измерения периода надо на горизонтальные пластины подать исследуемое напряжение и включить генератор развертки (вход Х), подающий пилообразное напряжение на вертикальные пластины. Вращая ручку «генератор развертки», получить на экране устойчивую картину– синусоиду. Посчитать количество клеток периода синусоиды и, помножив на цену деления генератора развертки, получить период колебаний.

Сложение однонаправленных гармонических колебаний

До сих пор мы изучали колебательные системы, для определения состояния которых требовалось знать закон изменения только одной величины. Для математического или физического маятников это смещение или угол отклонения . Для колебательного контура – заряд и т. д. Это системы с одной степенью свободы. Каждая из этих систем характеризуется одной собственной частотой колебаний.

Числом степеней свободы называется число независимых величин, с помощью которых однозначно определяется состояние системы.

В природе существует множество колебательных систем, так или иначе связанных друг с другом. В механике, например, такую систему с двумя степенями свободы образуют два математических маятника массой и длиной , связанные невесомой пружиной с коэффициентом жесткости (рис. 10.).

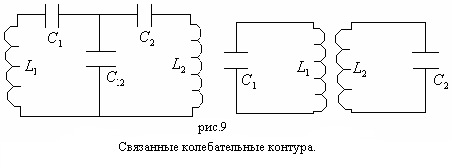
В электродинамике аналогом двух связанных маятников является электрическая цепь, состоящая из двух колебательных контуров , связанных общей емкостью или связанные индуктивно (рис. 9).

Колебательные системы, между которыми имеется связь, посредствам которой они взаимодействуют друг с другом, называются связанными. Это системы с двумя степенями свободы. Для задания их состояния требуется две величины. В отличии от одиночного маятника, уединенного контура, эти системы имеют две собственные частоты.

В общем случае движение системы с двумя степенями свободы очень сложно, непохожее на простое гармоническое колебания. Однако можно показать, что при линейных уравнениях движения это сложное движение связанной системы с двумя степенями свободы может быть представлено как суперпозиция двух независимых простых гармонических колебаний, происходящих одновременно. Эти простые гармонические колебания, с помощью которых может быть представлено сложное движение связанной системы, называется нормальными или собственными колебаниями, или гармониками, или нормальными модами, или простыми модами. Частоты, соответствующие этим гармоникам или модам, называются нормальными частотами.

Задавая определенные начальные условия, можно в связанной системе возбудить колебания, соответствующие одной нормальной моде или гармонике.

Связанные механические колебания

В случае двух связанных маятников первая мода возникает, если в системе возбудить синфазные колебания, а другая – при возбуждении антифазных колебаний.

Найдем частоты этих мод или нормальные частоты.

Для возбуждения синфазных колебаний оба связанных маятника отклоняют на одинаковый малый угол в одну и ту же сторону от положения равновесия (рис. 10). Воспользуемся основным законом вращательного движения вокруг неподвижной оси :

или

(15)

где – момент силы тяжести; – момент силы упругости; – момент инерции маятника относительно оси , – его угловое ускорение. Так как пружина не деформирована, сила упругости, а следовательно, и ее момент . Тогда равенство (15) в скалярной форме переписывается в виде:

(16)

Знак означает, что момент силы тяжести стремится вернуть маятник в положение равновесия. Так как , , где – масса маятника; – плечо силы тяжести, то равенство (16) можно представить в виде:

(17)

, а т. к. угол мал, то и , и (17):

(18)

Разделив обе части этого равенства на , получим дифференциальное уравнение гармонического колебания для величины :

(19)

где, очевидно, – есть квадрат циклической частоты синфазных колебаний. Подставив значение , где – длина маятника, получим , следовательно, частота синфазных колебаний:

(20)

Рассмотрим антифазные колебания маятников, для чего разведем маятники в противоположные стороны на один и тот же небольшой угол . При этом пружина деформируется на величину (рис. 11).

Теперь кроме силы тяжести на маятник будут действовать силы упругости: .

В скалярной форме уравнение (15) имеет вид: (21)

Так как ,

где – расстояние от оси до связи (пружины);

– жесткость пружины. При малом уголе . Равенство (21) перепишется в виде:

(22)

Получили дифференциальное уравнение антифазных колебаний.

Здесь , или учитывается, что , – циклическая частота антифазных колебаний, а частота антифазных колебаний:

(23)

Таким образом, в рассмотренной системе возникают две нормальные моды с частотами и . Изменяя силу связи, т. е. и , можно получить очень близкие по частоте две нормальные моды. Если систему привести в движение произвольным образом, возникает сложное движение, которое будет суперпозицией двух близких мод: .

Положим начальные фазы ; если частоты складываемых колебаний близки, т. е. , то возникают так называемые биения. Эффект биения будет наибольшим, если . Тогда, используя формулу суммы косинусов , получим уравнение биения:

(23)

где – амплитуда биения, – циклическая частота биений, а – период биения.

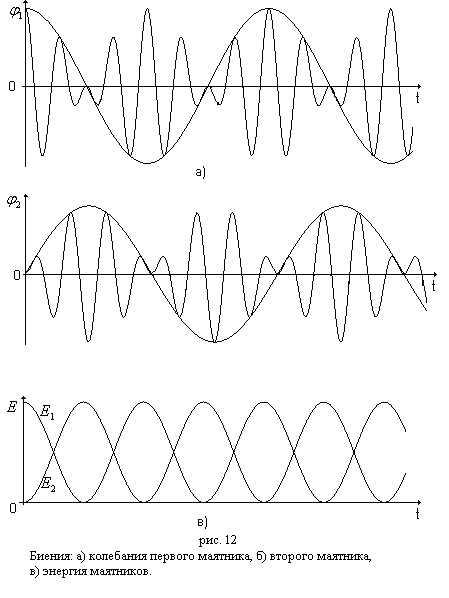
Графически биение 1-го маятника изображены на рис. 12а. Для возбуждения биения отклоним один маятник на , а второй будем удерживать в нулевой точке. Затем одновременно отпустим оба маятника. Амплитуда колебаний (а, следовательно, и энергия ) первого маятника уменьшается, а второго – возрастает (см. рис. 12б.). Через первый маятник остановится, а второй будет иметь амплитуду . При этом энергия колебаний переходит от одного маятника к другому полностью. Этот процесс будет периодически повторятся. Один полный оборот энергии от первого маятника ко второму и опять к первому и представляет одно биение (рис. 12в). Очевидно, что этот полный оборот энергии колебаний происходит за время, равное периоду биения . Если – циклическая частота биения, то частота биения:

(24)

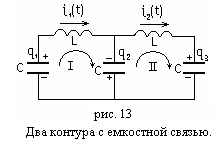
Связанные электромагнитные колебания

Примером системы с двумя степенями свободы является схема из двух электрических контуров с емкостной связью между ними (рис.13) Величина определяет степень взаимной связи контуров.

Рассмотрим влияние емкости связи на характеристики результирующего колебания. Полагаем для простоты контуры одинаковыми. Если емкость связи замкнута, контуры взаимно независимы и колебания, например, зарядов на каждой из емкостей описывается уравнением:

(25)

где – собственная частота колебательных контуров. Изменение зарядов описывается гармоническими функциями:

(26)

Если емкость связи отключена, то схема рис. 13 представляет собой единичный колебательный контур с индуктивностью и емкостью , резонансная частота которого равна .

Введение элемента связи меняет характер электрических связей в каждом из контуров. Однако, можно показать, что сложное колебание, происходящее в системе может быть представлено как суперпозиция двух независимых гармонических колебаний, которые получили название нормальных или собственных колебаний системы. Частоты этих колебаний называются нормальными и могут быть не равны собственным частотам контуров, входящих в систему.

Выведем уравнения, описывающие систему связанных электрических контуров (рис. 13). В силу закона сохранения электрического заряда . Законы Кирхгофа для контуров I и II , направление обхода которых показано на рис. 13:

(27)

где , , -–напряжения на емкостях с зарядами соответственно.

Для уменьшения числа неизвестных в системе уравнений (27) используем соотношения: , .

Система уравнений (27) принимает вид:

(28)

Систему связанных уравнений (28) относительно функций времени можно преобразовать в два независимых уравнения, это позволяет упростить решение задачи. Для этого каждое уравнение системы (28) разделим на и вначале сложим, потом вычтем:

(29)

Решение уравнений (29) может быть найдено в виде:

(30)

где амплитуды колебаний для удобства обозначены и , частоты колебаний определяются формулами:

(31)

Используя (6) можно найти искомые функции времени для зарядов:

(32)

Таким образом, колебания зарядов в каждом из контуров может быть представлено в виде суммы двух гармонических колебаний с частотами и , которые называются нормальными. Значения переменных величин в произвольный момент времени определяются начальными условиями . Выпишем начальные значения зарядов и токов, используя (32) и определение силы тока :

(33)

Рассмотрим различные способы возбуждения колебаний в системе.

С инфазные колебания. Пусть в начальный момент времени заряды на емкостях равны, а знаки соответствуют рис. 13, то есть

.

Этот случай соответствует синфазным колебаниям: в обоих контурах происходят колебания с нормальной частотой , совпадающей с собственной частотой каждого из контуров . В этом случае в произвольный момент времени заряд на емкости и ток через элемент связи не протекает. Колебания происходят так, как если бы отсутствовал участок цепи, содержащий емкость связи (рис. 14).

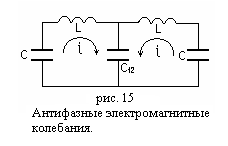Антифазные колебания. Пусть в начальный момент времени заряды на емкостях одинаковы, причем верхние пластины заряжены положительно, то есть . В этом случае токи равны по величине и противоположны по направлению (рис. 15).

Биения. Пусть в начальный момент времени заряжена только одна из емкостей , то есть . Учитывая (33), а также для упрощения полагая начальные фазы , получим:

,

то есть . Тогда в любой момент времени:

Используя формулу суммы косинусов, получим решение в виде:

(34)

Из (34) видно, что колебания зарядов происходят с частотой , а амплитуда колебаний меняется при этом с частотой . Зависимость зарядов на конденсаторах от времени показана на рис. 16.

В начальный момент времени вся энергия сосредоточена в первом колебательном контуре, в котором происходят колебания с частотой . За счет элемента связи вся энергия постепенно передается во второй колебательный контур до тех пор, пока вся энергия не будет сосредоточена во втором колебательном контуре. Затем начинается обратный переход энергии в первый контур. Время перехода энергии из первого контура во второй и обратно можно получить из уравнения (34):

Отсюда частота, с которой колебательные контуры обмениваются энергией, равна:

.

Таким образом, при заряде одной из емкостей в каждом из колебательных контуров осуществляется сложное колебание, характеризуемое периодическими изменениями амплитуды, биения. Биения наблюдаются также при сложении однонаправленных колебаний с близкими частотами (см. лабораторную работу №76).

При слабой связи между контурами частота обмена энергией

Период биений: ,

Где – период собственных колебаний в контуре.

Аналогичные результаты могут быть получены для токов дифференцируя формулы (8), (10) по времени ; для напряжений на емкостях . Связанные колебания удобно изучать, исследуя токи , напряжения на активных сопротивлениях, специально вводимых в схему. Наличие активных сопротивлений в схеме приводит к затуханию энергии и проявляется в уменьшении амплитуды огибающей (см. рис. 16).

Приложение 2