Міністерство освіти і науки, молоді та спорту України

Дніпропетровський національний університет імені Олеся Гончара

Громов В.О., Коряшкіна Л.С.

МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ЛАБОРАТОРНИХ РОБІТ

З КУРСУ «ОСНОВИ СИСТЕМНОГО АНАЛІЗУ»

Частина І. Моделювання і аналіз складних процесів, що описуються звичайними диференціальними рівняннями

Ухвалено Вченою радою університету

як методичні вказівки

Дніпропетровськ

РВВ ДНУ

2013

УДК 517.9

Рецензенти: д.т.н., проф. Н.І. Ободан

к.ф.-м.н., проф. С.А. Ус

Громов В.О., Коряшкіна Л.С.

Методичні вказівки до виконання лабораторних робіт з курсу «Основи системного аналізу». Частина І. Моделювання і аналіз складних процесів, що описуються звичайними диференціальними рівняннями. – Д.: РВВ ДНУ, 2013. – 99 с.

Методичні вказівки містять постановки завдань для лабораторних робіт з курсу «Основи системного аналізу», пов’язаних з використанням звичайних диференціальних рівнянь при вивченні реальних явищ та процесів. Наведений основний теоретичний матеріал, приклади складання диференціальних рівнянь і деякі методи дослідження їх якісної поведінки ілюструються задачами, що виникають в різних галузях знань. Для кожної лабораторної роботи представлений приклад оформлення звіту.

ЗМІСТ

Y

ВСТУП 5

Лабораторна робота № 1. Побудова фазових портретів лінійних і нелінійних систем 8

1.1. Постановка задачі 8

1.2. Основні теоретичні відомості. 8

Аналіз двовимірних динамічних автономних систем методом фазової площини 8

1.3. Використання пакетів прикладних програм для побудови поля напрямків і фазових траєкторій 24

1.4. Варіанти завдань 27

Лабораторна робота № 2. Біфуркації нерухомих точок динамічних систем 29

2.1. Структурна стійкість динамічної системи. Поняття точок біфуркації. Типові біфуркації 29

2.2. Побудова біфуркаційної множини у просторі параметрів сімейства динамічних систем 32

2.3. Типові біфуркації нелінійних динамічних систем 38

2.4. Приклад дослідження структурної стійкості динамічної системи 43

Розв’язання 44

Особливі точки. Знайдемо особливі точки системи (2.11): 44

Лінеаризація 45

Побудова біфуркаційної множини 46

Побудова біфуркаційної множини 48

Фазові портрети системи для заданих значень параметрів 50

Параметри, що належать області 1 50

Рис. 2.5. Фазовий портрет системи (2.11) для параметрів із області 1 50

Параметри, що належать області 2 51

Фазовий портрет нелінійної системи (2.11) за заданих параметрах: 51

51

Рис. 2.6. Фазовий портрет системи (2.11) для параметрів із області 2 51

Параметри, що належать області 3 52

Рис. 2.7. Фазовий портрет системи (2.11) для параметрів із області 3 52

Параметри, що належать області 4 53

Параметри, що належать області 5 54

2.5. Варіанти завдань 55

Лабораторна робота № 3. Аналіз катастроф 56

3.1. Постановка задачі 56

3.2. Основні теоретичні відомості. Типи катастроф. Класифікаційна теорема Тома 56

3.3. Приклад визначення катастрофи, що описується заданою функцією у виродженій критичній точці 78

3.4. Варіанти завдань 81

Лабораторна робота № 4. Побудова математичної моделі економічної, екологічної, соціальної системи та дослідження її поведінки 83

4.1. Постановка задачі 83

4.2. Основні принципи побудови математичних моделей динамічних 83

систем економіки, екології, соціології 83

4.3. Побудова моделі «хижак-жертва» і дослідження її динаміки 88

4.4. Варіанти завдань 97

СПИСОК ЛІТЕРАТУРИ 104

ВСТУП

“Natura scrita in lingua matematica” – “Природу написано мовою математики” - з цього щирого здивування Галілео Галілея бере початок уся новітня наука, принаймні європейська. Пройшло три століття – наші уявлення про навколишній світ та математичний апарат, яким ми послуговуємося, змінилися безмежно, але це здивування - здивування можливістю людського розуму за допомогою математичних категорій та формальних перетворень знаходити закономірності, що описують явища із різноманітніших царин людського знання – фізики, хімії, біології, економіки, соціології, лінгвістики тощо – раз-по-раз виринає із за сторінок сухих наукових статей та грубезних монографій. “Про дивовижну ефективність математики у природничих науках” - так назвав свій програмовий есей всесвітньо відомий фізик, Нобелівський лауреат Едвард Вігнер. “Щодо єдності математики чистої та прикладної” – це вже назва статті нашого співвітчизника, одного із засновників вітчизняної школи прикладної математики, академіка АН СРСР М. М. Моісеєва.

Ці методичні вказівки присвячені розгляду математичного апарату низки математичних теорій, що дозволяють виявити якісні аспекти феномена, що розглядається, - саме такі аспекти становлять предмет системноаналітичних студій: якісної теорії диференціальних рівнянь та теорії катастроф. Автори намагалися проілюструвати ці теорії прикладами із фізики, біології, екології, інших наук.

Математична модель – це спрощений опис реальності за допомогою математичних понять. Математичне моделювання – процес побудови і вивчення математичних моделей реальних процесів та явищ. Усі природничі і суспільні науки, які використовують математичний апарат, по суті займаються математичним моделюванням: замінюють реальний об’єкт його моделлю і досліджують останню. Як і у випадку будь-якого моделювання, математична модель не описує повністю явище, що вивчається, і питання про застосовність отриманих таким чином результатів є досить суттєвим (істотним).

Метою математичного моделювання є дослідження (хоч би на якісному рівні) поведінки системи, передбачення її поведінки у майбутньому і , за можливістю, керування процесом чи системою.

Математичне моделювання реального процесу або об'єкту складається з декількох етапів. Спочатку проводиться опис процесу на «змістовному» рівні, потім будується математична модель процесу. Ця модель досліджується, отримані для моделі висновки і результати звіряються з поведінкою реального процесу. Якщо отримані результати сильно розбігаються із спостережуваними фактами, модель слід або уточнити, або відкинути і будувати абсолютно нову. Досвід показує, що громіздка і складна модель не може бути адекватною дійсності. Всі фундаментальні закони природи (наприклад, закони Ньютона і знаменита формула Ейнштейна Е=mc²) мають простий і елегантний вигляд. Навчити будувати моделі неможливо, єдиної теорії моделювання не існує. Моделювання — не наука, а мистецтво. Щоб навчитися моделювати, треба вирішувати конкретні завдання.

Дана робота містить методичні вказівки до виконання лабораторних робіт з курсу «Основи системного аналізу». Тут розглядаються лише моделі, що описуються звичайними диференціальними рівняннями і їх системами. Під час побудови звичайних диференціальних рівнянь як моделей соціальних, економічних, екологічних процесів, важливе, а іноді й головне значення має знання законів той галузі, з якою пов’язана природа явища або процесу, що вивчається. Так, наприклад, в механіці це можуть бути закони Ньютона, в теорії електричних ланцюгів – закони Кирхгофа, в теорії хімічних реакцій – закон дії мас тощо. Звичайно, на практиці іноді виникають випадки, коли невідомі закони, що дозволяють скласти диференціальне рівняння, і тому вдаються до різних припущень (гіпотез), що стосуються протікання процесу. При цьому, якщо виявиться, що результати дослідження отриманого диференціального рівняння відповідають спостережуваним даним, то це й буде означати, що виказана гіпотеза справедлива (має місце на практиці).

Лабораторна робота № 1 стосується дослідження динамічних систем на стійкість, аналізу поведінки системи, побудови фазового портрету. Лабораторна робота № 2 присвячена теорії біфуркацій нелінійних динамічних систем. В лабораторній роботі № 3 виявляються катастрофи в системах, і досліджується їх тип. Лабораторна робота № 4 – комплексна, присвячена побудові математичної моделі конкретного динамічного процесу і дослідження її методами, що використовувались при виконанні попередніх лабораторних робіт.

Автори вдячні студенткам факультету прикладної математики Анастасії Хірі та Ользі Сазоновій за допомогу із набором тексту вказівок.

Лабораторна робота № 1. Побудова фазових портретів лінійних і нелінійних систем

1.1. Постановка задачі

Дана система звичайних диференціальних рівнянь:

1. знайти всі особливі точки системи;

2. визначити тип рівноваги і її стійкість;

3. зобразити фазовий портрет системи.

1.2. Основні теоретичні відомості.

Аналіз двовимірних динамічних автономних систем методом фазової площини

Метод фазової площини – це графоаналітичний метод дослідження нелінійних систем диференціальних рівнянь в деякому діапазоні початкових умов.

Метод дозволяє аналізувати нелінійні системи другого порядку і полягає у побудові фазових траєкторій (поданні динаміки системи диференціальних рівнянь рухом зображуючої точки на фазовій площині).

Нехай задана система:

(1.1)

Площина називається фазовою площиною. Стан системи в будь-який момент часу (або фаза руху) визначається парою чисел та зображується на фазовій площині точкою М. При зміні стану системи зображуюча точка описує у фазовому просторі траєкторію, яка називається фазовою траєкторією. Множина фазових траєкторій динамічної системи – її фазовий портрет.

Диференціальне рівняння фазових траєкторій отримаємо, розділивши друге рівняння на перше:

(1.2)

Фазові траєкторії будуються за розв'язком рівняння (1.2), якщо його можна знайти, або безпосередньо за рівнянням (1.2), використовуючи метод ізоклін. Ізокліною називається геометричне місце точок однакового нахилу фазових траєкторій до горизонталі, тобто точок, в яких:

(1.3)

Рівняння ізокліни:

(1.4)

За фазовим портретом можна судити про характер перехідних процесів в системі. Для цього потрібно: 1) знайти області стійкості; 2) визначити точки рівноваги; 3) оцінити перерегулювання та амплітуду коливань.

В точках рівноваги зображення точки М зупиняються. Точка рівноваги – це фазова крива, яка є фазовою точкою. Рівняння точок рівноваги:

Точки рівноваги називаються особливими, тому що в них нахил фазових траєкторій не визначений. Точка рівноваги може бути стійкою, якщо всі фазові траєкторії в околі особливої точки збігаються до неї, та нестійкою, якщо фазові траєкторії розбігаються від неї. Особливі точки класифікуються за характером фазових траєкторій в їх околі (див. рис. 1.1).

Рис. 1.1. Особливі точки: а – стійкий вузол; б – нестійкий вузол; в – стійкий фокус;

г – нестійкий фокус; д – сідло; е – центр

Правило руху зображуючої точки. Нехай система має вигляд:

.

Якщо , – зростає, точка рухається зліва направо. Якщо , – спадає, точка рухається справа наліво.

Зауваження: через кожну неособливу точку фазової площини для неперервних, всюди диференційовних, однозначних нелінійних функцій проходить єдина фазова траєкторія, тобто фазові траєкторії не перетинаються в неособливих точках.

Криві перехідного процесу. Відмітивши характерні точки, за даними фазовими траєкторіями можна побудувати відповідну криву перехідного процесу. Нелінійні системи характеризуються великим розмаїттям фазових портретів. Вони можуть мати декілька особливих точок. При наявності декількох точок рівноваги можливі різні типи фазових траєкторій:

• сепаратриси – особливі криві, що розділяють фазову площину на області з різними типами фазових траєкторій;

• граничні цикли – ізольовані замкнені криві, що відповідають періодичним режимам.

Ізоморфні замкнені траєкторії (граничні цикли) класифікуються за характером їх стійкості:

• стійкий граничний цикл – до якого зсередини і зовні збігаються фазові траєкторії (відповідає стійкому періодичному режиму – автоколиванням) (рис.1. 2,а).

• нестійкий граничний цикл – від якого зсередини і зовні фазові траєкторії віддаляються (рис 1.2,б).

• напівстійкі граничні цикли – наведені на рис. 1.1,в,г.

Рис1.2. Граничний цикл: а — стійкий; б — нестійкий; в, г — напівстійкий

Таким чином, метод фазової площини дозволяє визначити число, типи та характер особливих точок; ізолювати замкнені траєкторії; знайти сепаратриси; наочно представити усю сукупність рухів, що виникають в динамічних системах за будь-яких початкових умов.

Дослідження поведінки динамічних систем

Розглянемо систему (1.1) у двовимірному випадку. Через кожну точку фазової площини проходить єдина фазова крива, за виключенням особливих точок , таких що

Лінеаризуємо систему в околі точки рівноваги . Процедура лінеаризації (1.1): . В новій системі координат положенню рівноваги відповідає точка (0,0). Якщо f і g – аналітичні функції поблизу , то можна розкласти f і g в ряд Тейлора в околі цієї точки. Зважаючи на те, що в точці рівноваги , та знехтувавши величинами більш за першого за перший порядок малості, отримаємо лінеаризовану в околі систему відносно змінних :

Введемо позначення:

.

Розв'язки лінійної системи

(1.5)

дають параметричні (t – параметр) форми фазових кривих поблизу нерухомої точки .

Нехай та – власні значення матриці А, тобто

. (1.6)

Отже, розв’язки (1.5) мають вигляд:

(1.7)

де – довільні константи, а – власні вектори матриці А, які відповідають і визначаються за формулою:

(1.8)

Виключення параметра t в (1.7) дає фазові криві на площині (x,y) поблизу точки рівноваги . Вираз (1.7) використовується, якщо власні значення не є рівними. Якщо ж , то розв’язки (1.5) будуть пропорційні .

Далі розглянемо вплив власних значень матриці А на характер особливої точки лінійної системи (1.5). Для спрощення викладення вважатимемо, що точкою рівноваги є (0,0).

I) є дійсними числами і не дорівнюють один одному.

а) і мають однаковий знак. Типові власні вектори зображені на рис. 1. 3,а. Нехай Тоді, згідно з (1.7), наприклад, при справедливий вираз . Значить, точка на фазовій площині рухається лише уздовж у напрямку початку координат при : якщо – уздовж PО; якщо – уздовж QO. Згідно з (1.7), кожний розв’язок наближається до (0,0) при , тому що при коли . Отже ~ при .

Таким чином, поблизу початку координат всі розв’язки наближаються до нуля уздовж , як зображено на рис. 1.3,а. Така особлива точка називається вузол (тип I). Якщо , це буде стійкий вузол, оскільки всі траєкторії наближуються до (0,0) при . Якщо , це – нестійкий вузол; оскільки при (рис. 1.3,б).

Рис.1.3. Особлива точка – вузол: а – стійкий, б – нестійкий

б) і мають різні знаки. Припустимо, наприклад, що . Тоді, уздовж при , в той час як уздовж при .

Таким чином, рух уздовж і відбувається в різних напрямках; розв’язки поблизу (0,0) зображені на рис. 1.4,а. Така точка рівноваги називається сідловою точкою. Вона завжди нестійка, за виключенням руху строго вздовж напрямку вектора.

II) і є комплексними числами: Розв’язок (1.7) в цьому випадку включає в себе і, отже, коливально наближується до точки (0,0) або віддаляється від неї.

а) . В цьому випадку виникає точка рівноваги фокус, який є стійким при і нестійким при . На рис. 1.4,б зображена особлива точка на кшталт фокуса.

б) . В цьому випадку фазові криві представляють собою еліпси. Така особлива точка – центр; її зображено на рис 1.4, в.

У випадку особливих точок такого типу, знайдених за допомогою лінійного наближення функцій і , необхідно розглядати члени більш високого порядку (ніж лінійні) для того, щоб визначити, стійкі вони чи ні.

Рис.1.4. Особлива точка: а – сідло, б – фокус, в – центр

ІІІ) .

а) Розв'язки включають члени типу і в даному випадку існує тільки єдиний власний вектор , уздовж якого розв'язки прямують до (0,0). Параметр у виразі впливає на поведінку розв'язку далеко від (0,0). Ця точка називається вузол (тип ІІ); вона зображена на рис. 1.5,а.

б) Якщо розв'язки не включають члена , то особлива точка називається діакритичною, і може бути як стійкою, так і нестійкою залежно від знака . Траєкторії поблизу діакритичної особливої точки наведено на рис. 1.5,б.

Рис.1.5. Особлива точка: а – вузол (тип ІІ), б – діакритична

Таким чином, тип особливою точки залежить від параметрів в матриці А в (1.5). На рис. 1.6 підведений підсумок викладеним вище результатам в термінах сліду і визначника матриці А.

Рис. 1.6. Підсумкова діаграма, яка демонструє вплив сліду = і визначника на характер особливої точки

Теорема про декомпозицію багатовимірних систем

Дві динамічні системи

= f₁ (x) (1.9)

і

= f₂ (x) (1.10)

(f₁, f₂: R_n → R_n) з нульовою стаціонарної точкою називаються локально топологічно еквівалентними, якщо знайдеться такий певний в деякому околі нуля фазового простору гомеоморфізм h, що

h [g^t₁ (x)] = g^t₂ [h (x)]

при всіх t і x, при яких обидві частини тотожності мають сенс; тут g^t₁ і g^t₂ – відповідні оператори зсуву. Таким чином, гомеоморфізм h переводить траєкторії першої системи в траєкторії другої, причому, узгоджено (див. рис. 1.7). Якщо h визначений на всьому фазовому просторі, то слово "локально" у визначенні локальної топологічної еквівалентності опускають.

Рис. 1.7. Переведення траєкторії системи (1.9) у траєкторії системи (1.10) за допомогою гомеоморфізму

Нехай А – лінійний оператор, А: R_n → R_n, що задає лінійне рівняння

= Ax.

Припустимо, що власні значення оператора А попарно різні, серед них є деяке число дійсних чисел і деяке число комплексно спряжених пар, причому , та, що парність кількості дійсних власних чисел дорівнює парності . Тоді справедлива

Теорема [2]: Простір R_n розпадається в пряму суму інваріантних відносно А одновимірних і інваріантних відносно А двовимірних підпросторів.

Тобто у випадку, коли всі власні значення оператора А: R_n → R_n прості, лінійне диференціальне рівняння = Ax розпадається в прямий добуток рівнянь з одновимірними і двовимірними фазовими просторами.

Лінійна система = Ax називається гіперболічною, якщо матриця A не має власних значень на уявній осі. Справедлива

Теорема. Дві гіперболічні системи = A₁x і = A₂x топологічно еквівалентні, якщо і тільки якщо кількість n_–(A₁) і n_–(A₂) власних значень з від’ємною дійсною частиною з урахуванням кратності (а отже, і кількість n₊(A₁) і n₊(A₂) власних значень з додатною дійсною частиною) матриць A₁ і A₂ збігається: n_–(A₁) = n_–(A₂), n₊(A₁) = n₊(A₂).

З теореми, наприклад, випливає, що двовимірні гіперболічні системи розбиваються на три топологічно не еквівалентні класи: а) стійкі вузли і фокуси, б) сідла; в) нестійкі вузли і фокуси.

Рис. 1.8. Топологічно еквівалентні і нееквівалентні системи

Перейдемо до питання про структуру околу стаціонарної точки нелінійної динамічної системи. Обмежимося випадком динамічної системи з диференційовною правою частиною

= f (x) (1.11)

(f ∈ C₁ (R_n, R_n), f (0) = 0), причому будемо припускати, що лінеаризована в нульовій точці стаціонарна система

= Ax (1.12)

(A = f'(0)) – гіперболічна. У цьому випадку відповідь на питання про поведінку траєкторій в околиці нульової стаціонарної точки дає фундаментальна

Теорема Гробмана - Хартмана. Динамічна система (1.11) локально топологічно еквівалентна своєї лінійній частині (1.12).

Повний аналіз питання про стійкість розв’язку рівняння (1.12) можна виконати безпосередньо аналізуючи поведінку матричної експоненти .

Нехай - повний набір коренів характеристичного рівняння матриці А.

Якщо всі власні значення матриці А мають від’ємні дійсні частини, то тривіальний розв’язок рівняння (1.12) асимптотично стійкий.

Якщо хоча б один з коренів характеристичного рівняння матриці А має додатну дійсну частину, то тривіальний розв’язок рівняння (1.12) нестійкий.

Нехай серед коренів характеристичного рівняння матриці А є декілька коренів з нульовою дійсною частиною, в той час коли решта коренів мають від’ємні дійсні частини. Тоді:

а) якщо всім кореням з нульовою дійсною частиною відповідають прості елементарні дільники, то тривіальний розв’язок рівняння (1.12) стійкий, але не асимптотично;

б) якщо хоча б одному з коренів із нульовою дійсною частиною відповідає кратний елементарний дільник, то тривіальний розв’язок системи (1.12) нестійкий.

Доведення цих умов стійкості тривіального розв’язку системи (1.12) див. у [15].

Нехай А – лінійний оператор, А: R_n → R_n, що задає лінійне рівняння

= Ax.

Припустимо, що власні значення оператора А попарно різні, серед них є деяке число дійсних чисел і деяке число комплексно спряжених пар, причому , так, що парність кількості дійсних власних чисел дорівнює парності . Тоді справедлива

Теорема [2]: Простір R_n розпадається в пряму суму інваріантних відносно А одновимірних і інваріантних відносно А двовимірних підпросторів.

Тобто у випадку, коли всі власні значення оператора А: R_n → R_n прості, лінійне диференціальне рівняння = Ax розпадається в прямий добуток рівнянь з одновимірними і двовимірними фазовими просторами. І тому дослідження стійкості особливих точок довільної системи виду (1.11) зводиться до дослідження особливих точок одновимірних і (або) двовимірних динамічних систем.

1.2.4. Приклади побудови фазового портрету лінійної і нелінійної системи

Для побудови фазового портрету лінійної динамічної системи:

необхідно виконати наступні дії:

1. Обчислити detM, де , знайти власні значення матриці М та обчислити trM . Визначити тип особливої точки згідно викладеного у попередньому параграфі матеріалу.

2. Знайти рівняння особливих напрямків (dx/dt)=0 та (dy/dt)=0

y=(-a/b)x, y=(-c/d)x.

3. Якщо особлива точка є сідлом або вузлом, то знайти асимптоти, використовуючи підстановку y=kx.

4. Визначити напрямки фазових траєкторій.

Приклад 1: дослідити характер особливої точки (0,0):

(1.13)

1. Обчислюємо визначник і слід матриці М: .

Особлива точка (0,0) – сідло. Про цей факт свідчать і корені характеристичного рівняння : .

2. Рівняння особливих напрямків: y=(4/5)x; y=2x. Першу пряму фазові траекторії перетинають у вертикальному напрямку, а другу – горизонтальному.

3. Знаходимо рівняння асимптот. Нехай y=kx. Розв'язуючи рівняння відносно k: k=(–2+k)/(4–5k), знаходимо кутові коефіцієнти асимптот: у=(-2/5)x; y=x.

4. Визначаємо напрямки фазових траєкторій, враховуючи знак похідних і в точках фазових траєкторій.

Рис. 1.9. Поле напрямків системи (1.13) Рис. 1.10. Фазові траєкторії системи (1.13)

Приклад 2: знайти всі нерухомі точки нелінійної системи і дослідити їх

на стійкість

. (1.14)

Особливі точки системи знайдемо, розв'язуючи систему рівнянь:

Особливі точки: =(1;-1); =(1;1); =(2;-2); =(2;2).

Запишемо вирази частинних похідних функцій і :

Визначимо тип кожної особливої точки.

1. =(1;-1) – стійкий вузол. Дійсно, лінеаризуючи систему у околі цієї точки, приходимо до системи лінійних диференціальних рівнянь відносно збурень фазових координат:

. (1.15)

На рис. 1.11 наведені фазові траєкторії і поле напрямів цієї системи.

Рис. 1.11. Фазові траєкторії і поле напрямків системи (1.15)

2. =(1;1) – сідло. Лінійна система відносно лінеарізованих фазових змінних в точці (1,1) має вигляд:

(1.16)

На рис. 1.12 наведені фазові траєкторії і поле напрямів цієї системи.

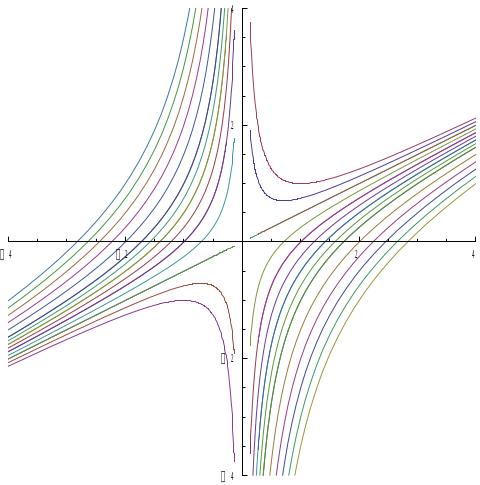
Рис. 1.12. Фазові траєкторії і поле напрямків системи (1.16)

3. =(2;–2) – також є сідлом. Лінійна система диференціальних рівнянь відносно збурень фазових координат в точці має вигляд:

Фазові траєкторії і поле напрямів в цій точці наведені на рис. 1.13.

Рис. 1.13. Фазові траєкторії і поле напрямків системи (1.14) у околі точки (2;–2)

4. =(2;2) – нестійкий фокус, тому що в лінійній системі диференціальних рівнянь відносно збурень

; ; (корені характеристичного рівняння: ). Фазові траєкторії і поле напрямів наведені на рис. 14.

Рис. 1.14. Фазові траєкторії і поле напрямків в точці системи (1.14) у околі точки (2;–2)

Фазовий портрет динамічної системи (1.10) представлений на рис. 1.15.

Рис. 1.15. Фазовий портрет системи (1.14)