ВВЕДЕНИЕ

1. Определения.

Пусть дано поле . Множество с операциями сложения и умножения на элементы поля называется векторным (линейным) пространством над полем , если выполнены следующие свойства:

1 - абелева группа по сложению.

2 Определено умножение скаляров из поля на элементы , результатом этого умножения является новый элемент , причем:

• ;

• ;

• ;

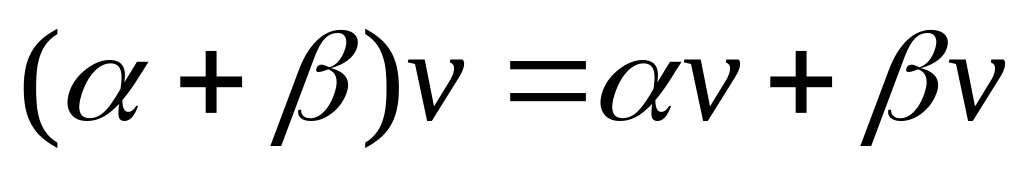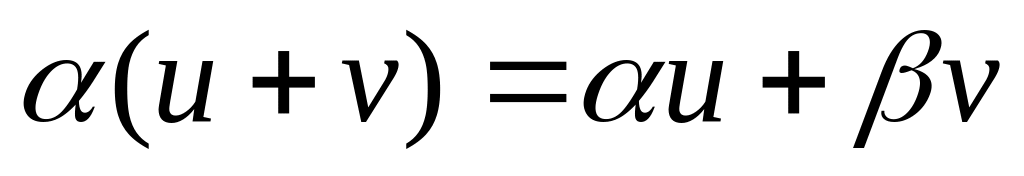где

3 В поле есть единичный скаляр .

Опр. Вектором называется элемент векторного пространства.

2. Линейная зависимость.

Векторы называются линейно зависимыми тогда и только тогда, когда (не все равные 0), такие, что .

Следствие. линейно независимы тогда и только тогда, когда

Набор векторов будем называть базисом , если

1 такие, что .

2 линейно независимы.

Предложение 1. Пусть и - два базиса пространства. Тогда .

Разложим векторы первого базиса по второму базису . Если строчки скаляров линейно зависимы, то зависимы и (так как можно взять их линейную комбинацию с теми же коэффициентами, что обнуляют строки вида ). Так как число линейно-независимых строчек не превосходит , то . Аналогично

Опр. Размерностью пространства будем называть число векторов в любом базисе . Обозначается .

Предложение 2. Базис – максимальная линейно независимая система векторов (максимальная – значит наибольшая по включению).

Действительно, пусть есть вектор, который будучи добавленным к базису, образует вместе с ним по-прежнему линейно независимую систему. Но тогда этот вектор не выражается через вектора базиса! Обратно, если дана максимальная линейно независимая система, то она является базисом, так как любой другой вектор выражается через ее вектора (иначе можно было бы дополнить систему этим вектором).

Предложение 3. линейно независимых векторов.

Будем дополнять систему векторов до базиса. Этот процесс будет продолжаться сколь угодно долго (т.к. иначе пространство имеет конечную размерность). А так как система будет всегда линейно независима, то имеем систем линейно-независимых векторов сколь угодно большой длины.

4. Матрицы перехода от базиса к базису.

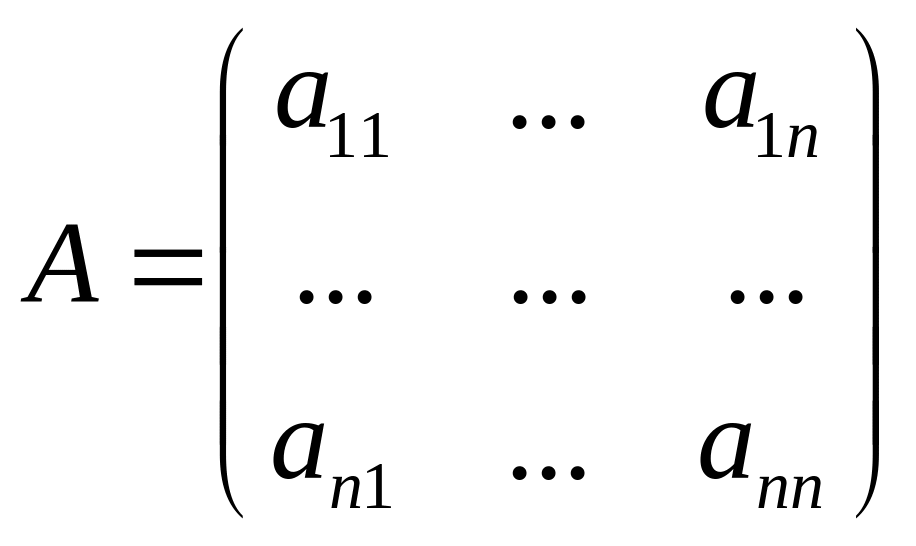Пусть - два базиса . Тогда существуют скаляры такие, что . Тогда матрица называется матрицей перехода от базиса к базису .

Свойства матрицы :

1 -тый столбец матрицы - столбец координат вектора в старом базисе (нештрихованном).

2 .

Задача. Известны матрицы перехода от первого базиса ко второму и от второго базиса к третьему B. Доказать, что матрица перехода из первой системы в третью .

07.02.05

5. Координаты в различных базисах.

Пусть и - два базиса , .

Теорема.

, где - матрица перехода от нештрихованной системы к штрихованной.

.

6. Изоморфизм векторных пространств.

Отображение , где и - векторные пространства над одним и тем же полем называется изоморфизмом, если для любых

1) .

2) - биекция

Замечание. Ноль переходит в ноль (так как ), и только он, так как преобразование биективно.

Теорема. Конечномерные векторные пространства и изоморфны .

Пусть , - базис в , тогда - базис в . Действительно, пусть эти вектора линейно зависимы, т.е.

Значит, единственная нулевая линейная комбинация является тривиальной, то есть - действительно базис.

Пусть .