Тема 8. Вимірювання часу життя та дифузійної довжини нерівно вісних носіїв заряду (лекції №29,30)

Нестаціонарні методи

У нестаціонарних (кінетичних) методах зазвичай вивчається релаксаційний процес переходу напівпровідника з рівноважного в нерівноважний стан або зворотний перехід при інжекції в напівпровідник надлишкових носіїв заряду (використовується фотоінжекція або інжекція струмом через неомічний контакт). Характеристики процесу рекомбінації, в простому і найчастіше випадку, що зустрічається, це час життя, знаходяться з порівняння теорії і експерименту.

Теорія рекомбінації оперує з концентрацією носіїв заряду — диференціальною величиною, а при вимірах визначаються які-небудь інтегральні величини, наприклад провідність всього зразка. Тому в задачу теорії кожного методу дослідження, в якому вимірюється та або інша інтегральна величина, входить визначення зв'язку між безпосередньо вимірюваною інтегральною характеристикою і диференціальними характеристиками.

Розглянемо простий і часто вживаний метод дослідження процесів рекомбінації, в якому відомості про них отримують по осцилограмі фотопровідності ∆Σ при освітленні зразка одиночними або періодичними прямокутними імпульсами світла. Типова схема вимірів приведена на рис. 1, а, де послідовно із зразком з опором R включені джерело напруги ІН і опір навантаження R_н . При освітленні зразка імпульсом світла на R_н виникає змінна напруга ∆U_н, яка після посилення підсилювачем У поступає на вхід осцилографа N. Напруга

Опір R_н вибирається так, щоб дотримувалася пропорційність між ∆U_н і ∆Σ.

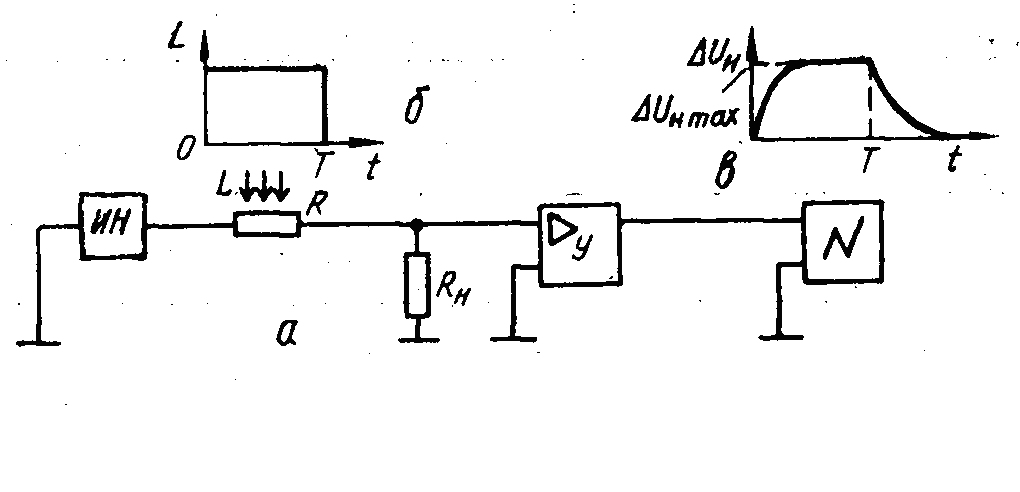
Рис.1. Схема установки для дослідження кінетики фотопровідності (а), форма імпульса світла (б), осцилограма напруги (в)

При малому рівні інжекції | ∆R | « R₀, величиною ∆R у знаменнику (7.8) можна нехтувати і при будь-якому R_н напруга ∆U_н ~ ∆Σ. При довільному рівні інжекції така пропорційність буде реалізована лише при

R_н<< R, коли величиной R„ в знаменнику вираження (7.8) можна нехтувати і

Дослідження релаксації фотопровідності в різних умовах, наприклад при різній інтенсивності світла, його спектральному" складі, при постійному підсвічуванні, різних температурах, дає обширну інформацію про процеси рекомбінації в напівпровідниках. Нижче обмежимося простим випадком визначення часу життя τ при ∆n = ∆р і лінійною рекомбінацією носіїв, коли справедливе рівняння

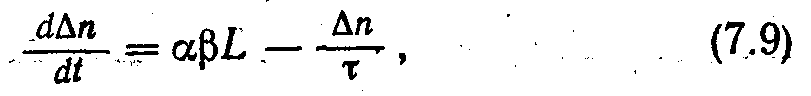
де α - коефіцієнт поглинання світла; β— квантовий вихід; L — інтенсивність світла. Для прямокутних імпульсів світла з амплітудою L₀ і тривалістю Т (рис. 1, б) рішення (7.9) дає після закінчення дії імпульсу

∆n=αβL₀τ[1 – exp(-T/τ)]exp[(t-T)/τ.

Якщо Т >>τ, то за час дії імпульсу встигає встановитися стаціонарне значення концентрації ∆n=αβL₀τ.

Інжекція нерівноважних носіїв заряду імпульсом струму. Розглянемо біполярну інжекцію в зразок n- типу, в якого контакт при х = 0 інжектуючий з коефіцієнтом інжекції дірок γ, а при х = а — омічний. Через зразок починаючи з t = 0, в напрямів від першого контакту до другого пропускається імпульс струму з амплітудою І₀ і тривалістю Т. Уровень інжекції малий, а напруженість електричного поля в зразку досить велика для зневаги дифузійними складовими струмів.

Під час дії інжектуючого імпульсу напруга на зразку

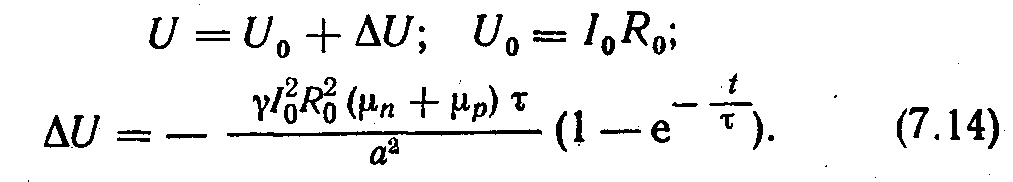
По осцилограмі ∆U можна визначити τ, а по амплітуді другого доданку, вимірявши R₀, а також вимірявши або узявши з таблиць μ_n і μ_p, можна знайти γ. При τ > t _пр(де t_пр- час проліту носіїв заряду) на осцилограмі ∆U повинні спостерігатися злам і перехід до насичення. Вимірявши t_np, можна знайти μ_p.

Особливістю даних вимірів є те, що в них потрібно реєструвати малий сигнал ∆U на тлі більшого U₀. Виділення ∆U можна провести за допомогою обмежувача напругу. Такі схеми прості і тут не розглядаються. Опишемо лише виділення ∆U за допомогою моста, приведеного на рис. 2, а. У нім в одну діагональ включений генератор прямокутних імпульсів ГИ, а в другу — підсилювач У і осцилограф N. Зміна опору зразка при інжекції | ∆R | <<R₀ + R₁, тому через зразок проходять імпульси струму. Хай перемикач П знаходиться в положенні 1. Зміною опору R₂ збалансуємо міст у момент початку імпульсу. При інжекції виникає розбаланс і на екрані осцилографа спостерігається сигнал, пропорційний ∆U. На рис. 2, б змальовано дві типові осцилограми ∆U при різних τ.

Розглянемо тепер роботу схеми, коли перемикач П знаходиться в положенні 2.

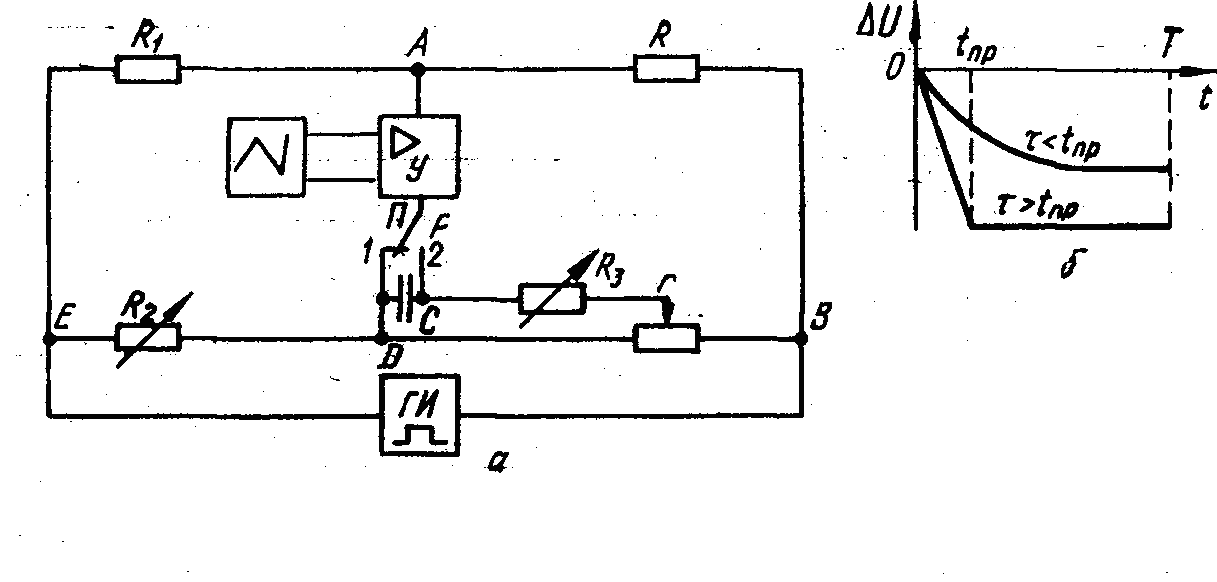
Рис.2. Схема моста для вимірювання часу життя (а) і і типова осцилограма (б)

Використовуючи (7.14), записуємо для напруги U на зразку, що реалізовується

в схемі між крапками А і В,

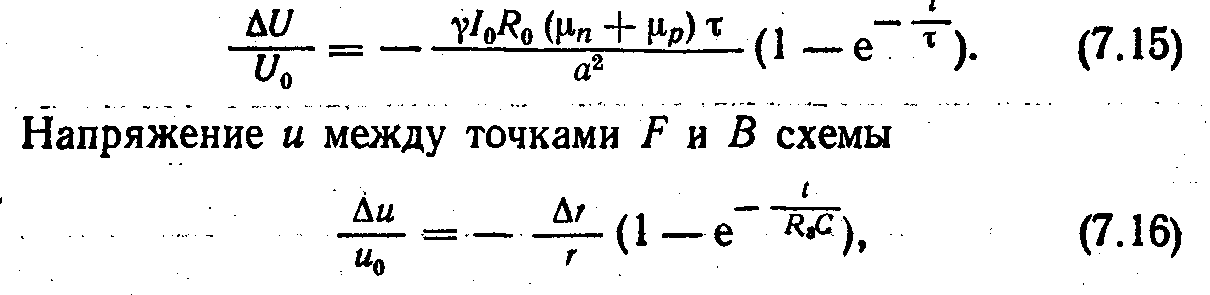
де індекс «0» відзначає значення напруги у момент початку імпульсу струму t= 0; ∆г — опір ділянки резистора г від движка до точки D, г << R₃. Зміною R₂ можна добитися рівності напруги U і u у момент t = 0 (U₀ = u₀),

а потім зміною ∆г і R₃ добитися балансу моста в подальші моменти часу. При

балансі звідки можна визначити τ і γ.

Інжекція через точковий контакт

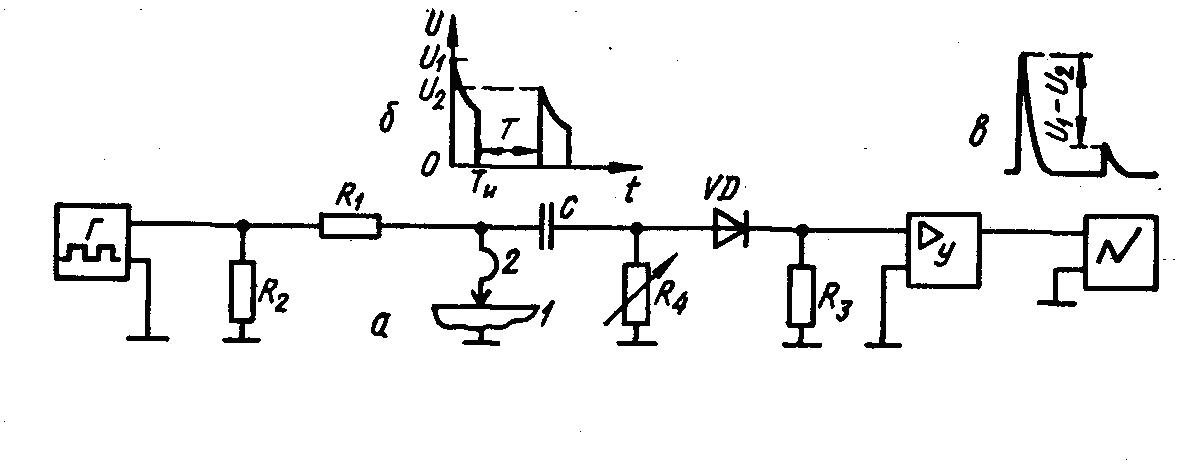
Рис. З. Схема установки для вимірювання часу життя (а), вид імпульсів напруги (б), осцилограма напруги (в)

Розглянуті вище методи виміру часу життя реалізуються для зразків правильної геометричної форми. В процесі виготовлення напівпровідникових матеріалів виникає завдання виміру часу життя безпосередньо на злитках. Такі виміри можна проводити методом, де на поверхню зразка (рис. 3, а) встановлюється точковий инжектирующий контакт 2. Через контакт пропускають імпульс струму з амплітудою І₀, який інжектує в зразок нерівноважні носії і змінює опір підконтактної області. Фіксують амплітуду U₁ напруги, що виникає на контакті імпульсу (рис. 3, б). Потім через проміжок часу Т після закінчення першого імпульсу пропускають другий імпульс струму з такою ж амплітудою І₀. Якщо Т ≤ τ, то до моменту приходу другого імпульсу під контактом є носії заряду, інжектовані першим імпульсом, і опір його менший, ніж у момент приходу першого імпульсу. Тому напруга U₂, що виникає у момент початку другого імпульсу, менше U1. Різниця U₁ — U₂ = f (Т, τ). Величину τ визначають із зіставлення експериментальної і теоретичної залежностей U₁ — U₂ від Т.

Стаціонарні методи

Основні параметри рекомбінаційного процесу — час життя τ, дифузійна довжина l_д, швидкість поверхневої рекомбінації s — визначають величину всіляких ефектів, що виникають в збуджуваному тим або іншим чином напівпровіднику. Відповідно, будь-який з таких ефектів може бути використаний для дослідження процесів рекомбінації.

Визначення τ по величині стаціонарної фотопровідності.

Збуджуючи зразок напівпровідника світлом в умовахі вимірюючи стаціонарне значення ∆Σ, можна знайти час життя, вважаючи, що вклад електронів і дірок в надлишкову провідність істотно неоднаковий. Допустимо, для визначеності, що μ_n∆N>> μ_p∆P, тоді із формули приросту провідності зразка ∆Σ=е/а²(μ_n∆N + μ_p∆P), знаходимо, що

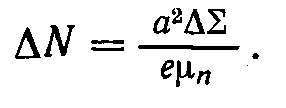
Величина ∆N дозволяє знайти час життя електронів τ_n , якщо надлишкові електрони рівномірно розподілені за об'ємом V зразка або його частини, то ∆N = ∆n_стV = αβІ₀ τ₀V, звідки

Методи безпосереднього визначення дифузійної довжини.

Величина l_д (а звідси, τ_n ) може бути знайдена з безпосереднього вивчення дифузії носіїв заряду в напівпровіднику. При цьому використовується локальне збудження зразка напівпровідника (наприклад, оптичним методом) і вивчається сталий в результаті дифузії розподіл надлишкових носіїв заряду. Значення l_д знаходиться із зіставлення результатів експерименту з теорією, яка будується на підставі вирішення рівняння дифузії

Метод світлового зонда визначення l_д

Зразок збуджується вузьким світловим штрихом (рис. 4), і вивчається розподіл надлишкових носіїв заряду в затемненій частині. Для визначення концентрації неосновних носіїв заряду на зразок ставлять голку (колектор, що формує випрямляючий контакт) і вимірюють струм колектора залежно від його відстані х до світлового штриха. На колектор подається зсув в замочному напрямі. При цьому його струм визначається концентрацією неосновних носіїв заряду в безпосередньо прилеглої області; залежність струму від концентрації, в першому наближенні можна вважати лінійною.

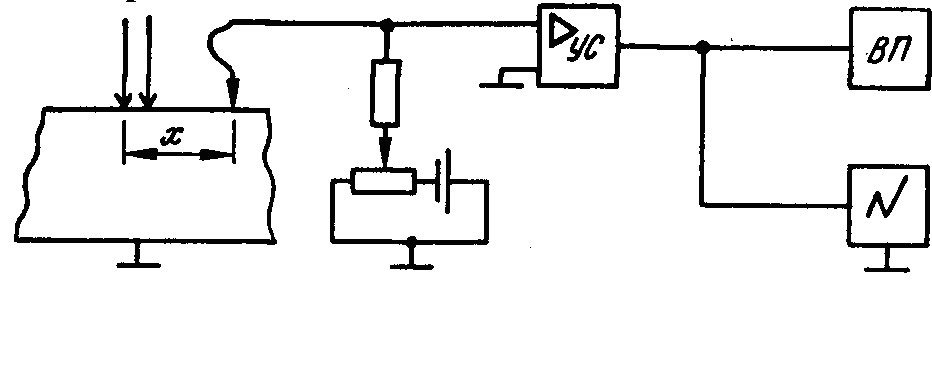
Рис.4. Установка для вимірювання l_д по методу світлового зонда

Теоретичні залежності ∆р (х) для тонкого зразка (товщина d << l_д)

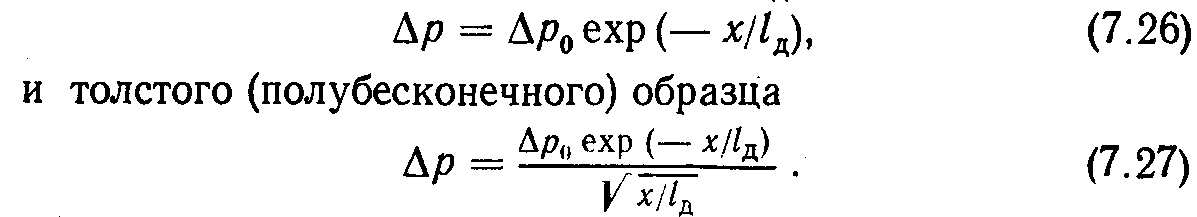
Величину х змінюють, переміщаючи світловий зонд. Для підвищення чутливості зазвичай застосовують модульований світловий потік і вузькосмуговий підсилювач; період модуляції повинен значно перевищувати τ_n.

Якщо струм колектора нелінійно (не однозначно) пов'язаний з величиной ∆р, застосовують метод постійної фотовідповіді. При цьому передбачається, що величина ∆р₀ (надлишкова концентрація в місці збудження) лінійно залежить від інтенсивності збуджуючого світла І₀; останню регулюють так, щоб при будь-якому х струм колектора був одним і тим же. Тоді для тонкого зразка

По припущенню ∆р₀ = αІ₀, де α— постійний коефіцієнт (ця умова означає, що τ_n не залежить від інтенсивності збудження; інакше l_д — l_д (І₀) і вся методика непридатна). Тоді

Отже, знаючи інтенсивність збудження, що забезпечує при різних відстанях постійну фотовідповідь на колекторі, можна знайти l_д і τ_n.

Тема.9. Визначення типу електропровідності напівпровідників та вимірювання питомого опору напівпровідників (лекції №31-34)

Тип електропровідності може бути визначений декількома методами.

Це наступні методи.

1.Метод термозонда. Цей метод оснований на виникнені термо – е.р.с. визначеної полярності на кінцях напівпровідникового кристалу, коли кінці його знаходяться при різних температурах. Знак термо – е.р.с. залежить від типу електропровідності вихідного матеріалу і тому може показником для визначення типу провідності.

2.Метод вольт-амперної характеристики на точковому контакті.

Визначення типу провідності цим методом основано на випрямляючих властивостях точкового контакту метал – напівпровідник. В електронному напівпровіднику (n-типу) прямий струм направлений від напівпровідника до металу, а в дірковому – в протилежному напрямі.

Визначення питомого електричного опору напівпровідників

Зондові методи

Існують контактні і безконтактні методи визначення питомого опору ρ. По-перше на поверхні зразка створюються металеві контакти, через два з яких пропускають струм І . Між цими або якими-небудь двома іншими контактами вимірюють створюване струмом I падіння напруги U = ρ·I·F, де F — функція форми і розмірів зразка і контактів, яку знаходять з теоретичного розрахунку. При відомій F по виміряних I і U обчислюють ρ. Простим методом такого типа є визначення ρ по повному опору зразка.

Хай напівпровідниковий зразок має форму бруска, на торці якого нанесені омічні контакти. Біля кордону розділу напівпровідника і металу може утворюватися запірний шар, концентрація носіїв заряду в якому менша, ніж в об'ємі напівпровідника. Тому цей шар володіє підвищеним опором. При омічному контакті відсутній такий шар або шар підвищеного опору якої-небудь іншої природи. Концентрація носіїв заряду однакова у всьому зразку, аж до кордону з металом, або в разі антизапірного шару в металі вона збільшується. Опір антизапірного шару менше опору шару такої ж товщини в об'ємі напівпровідника, проте, оскільки антизамочний шар має товщину багато меншу довжини зразка, то зменшенням опору зразка із-за існування в нім антизапірного шару можна нехтувати. Таким чином, при омічному контакті опір шару будь-якої товщини поблизу кордону металу і напівпровідника не більший, ніж шару такої ж товщини в об'ємі напівпровідника. Протікання через контакт струму не приводить до зміни концентрації носіїв заряду в напівпровіднику. Такі явища, як інжекція, екстракція, ексклюзія і акумуляція відсутні.

У даних умовах зв'язок струму і напруги між контактами визначається формулою

U/I =R=ρ(a/S), (1)

де R — опір зразка; а — довжина; S — площа поперечного перетину. Тут функція F має простий вигляд F =a/S. Вимірявши окремо U і I або відразу R, наприклад мостом опору, по (1) можна обчислити питомий опір р, що не викликає труднощів в разі зразків середнього значення опору з ρ = 10^-2...10⁶ Ом • см і низкоомних зразків з ρ< 10^-2 Ом • см. При цьому опір низькоомних зразків може бути порівнянний з опором струмопровідних дротів, що необхідно враховувати.

При вимірах на високоомних зразках, зазвичай з р > 10⁶ Ом • см, даний спосіб визначення питомого опору може бути ускладнений наявністю ємкісного струму, поляризаційними ефектами і поверх ностными витоками.

Двозондовий метод виміру питомого опору

Реалізація розглянутих в попередньому параграфі методів виміру питомого опору р вимагає створення на зразку омічних контактів, а в разі контактів з підвищеним опором ці методи дають завищені значення питомого опору. Такого недоліку позбавлені зондські методи.

Схема двохзондового методу виміру приведена на рис. 5.

На торці зразка нанесені контакти K₁ і К₂, а на його поверхні на відстані l один від одного встановлено два точкові зонди З₁ і 3₂. Між ними включений нульовий прилад Г і потенціометр П. В якості зондів можуть бути використані, наприклад, загострений провід.

Значення питомого опору визначається таким чином. Через зразок від джерела ИТ пропускають струм I, який вимірює прилад А. Потім, змінюючи напругу на потенціометрі П, добиваються відсутності струму через прилад Г. В цьому випадку напруга на потенціометрі П дорівнює падінню напруги, що створюється струмом I на ділянці зразка між зондами, тобто

де R — опір ділянки зразка між зондами; S — площа поперечного перетину зразка. З (3.8) обчислюється питомий опір ρ.

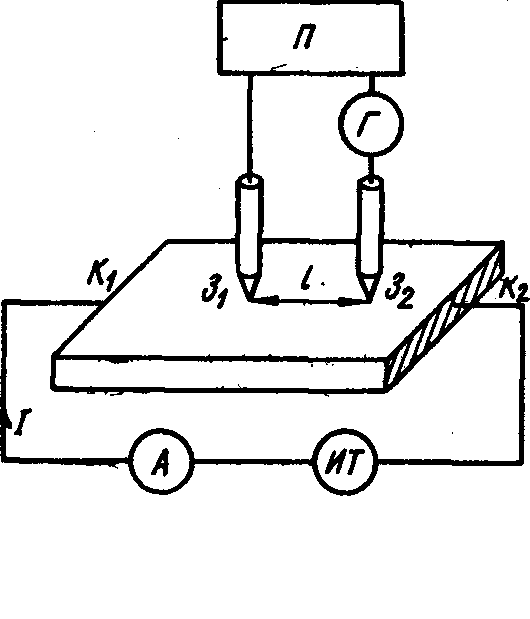
Рис.5. Схема вимірювання питомого опору двозондовим методом

Вимірювання питомого опору напівпровідника методом опору розтікання

Суттєвість цього методу в наступному. Відомо, що в області контакту металевого зонда з напівпровідником виникає контактний опір R_k, величина якого залежить від напряму струму. Об'єм напівпровідника між зондом і зворотним контактом задає струму деякий опір R_р, який називають опором розтікання і який залежить від величини питомого опору напівпровідника.

Площа зворотного контакту звичайно велика, тому він являється омічним, і величиною його опору у порівнянні з R_k можна знехтувати. Якщо зонд і зворотний контакт достатньо віддаленні один від одного , то еквіпотенціальні поверхні по мірі заглиблення в товщу напівпровідника міняють свою форму від початкової, яка визначається геометрією самого зонда, до плоскої поблизу зворотного контакту. При цьому силові лінії струму, перпендикулярні еквіпотенціальним поверхням, найбільш згущенні поблизу зонда і розходяться по мірі заглиблення у напівпровідник.

Тому більша частина R_р обумовлена тією частиною об'єму напівпровідника, яка примикає до зонду.

Зробивши предположення, що поверхня області контакту зонда з кристалом представляє собою плоский круг діаметром 2r, У. Шокли предложив просту формулу для визначення питомого опору напівпровідника:

ρ=4rR_р. (1)

На практиці звичайно використовуються зонди, які забезпечують точковий контакт, кінчик яких закруглений у формі на півсфери діаметром 2r. В цьому випадку розрахунок ρ проводитьться по дещо зміненній формулі:

ρ=2πrR^'_р, (2)

де R^'_р= R_k + R_р.

Сумарний опір R^'_р= R_k + R_р між зондом і зворотним контактом мже бути визначений відомими методами, наприклад, приклавши велику напругу в пропускному напрямі до контакту метал-напівпровідник, то можна знехтувати опором R_k і тоді R_k + R_р ≈ R_р і можна рахувати, що R_р буде пропорційний падінню напруги на структурі напівпровідника, тобто на її об'ємній області: R_р ≈ U/I. В такому разі формулу (2) можна записати в такому вигляді:

ρ=2πr(U/I), (3)

Таким чином, з урахуванням того, що в формулі (3) множник 2πr є величиною постійною, а струм І через зразок можна задати від джерела постійного струму постійним, величина ρ буде пропорційна падінню напруги на зразку, яке буде пропорційне концентрації легуючої домішки в ньому (тобто пропорційно ρ).

Однозондовий метод виміру питомого опору

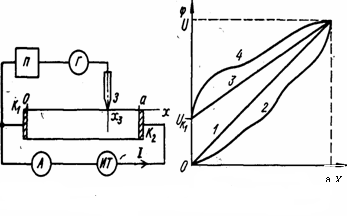
Рис.6.Схема вимірювання Рис.7.Типи розподілу потенціалу

однозондовим методом впродовж зразка

Схема однозондового методу виміру (рис.6) виходить з схеми двозондового, приведеного на рис. 5, якщо одну з клем потенціометра з'єднати з струмопровідним контактом. Встановлюваний на поверхні зонд 3 зроблений рухливим, тобто відстань х_з від токоподводящего контакту К1 до нього можна змінювати.

Провівши виміри падіння напруги φ між контактами К₁ і цим зондом при двох значеннях відстані х₃₁ і х₃₂, можна визначити величину питомого опору

по формулі

На рис. 7 приведені типи розподілу потенціалу впродовж зразка. Всі залежності на рис.7 відповідають зразкам з омічним контактом К₂ (рис.6) при х=а. Якщо цей контакт неомічний, то при х=а буде мати місце скачок напруги.

Чотирьохзондовий метод вимірювання питомого опору

У всіх розглянутих вище методах виміру питомого опору потрібні зразки правильної і сповна визначеною форми. Проте в умовах виробництва часто виникають завдання, коли цю умову не можна виконати. Наприклад, якщо потрібно взнати опір матеріалів у різних ділянках напівпровідникового злитка, не порушуючи його цілісність, або визначити питомий опір матеріалу в пластині неправильної геометричної форми. Такі завдання привели до розвитку спеціальних методів визначення питомого опору, що не пред'являють жорстких вимог до геометрії використовуваних зразків. До них відносяться методи, описані в цій та наступних розділах. Хай на поверхню зразка встановлено чотири точкові зонди, як це показано на рис. 8. Відстань між сусідніми зондами s, через два крайні зонди 1 і 4 проходить струм I, який створює деяку різницю потенціалів U між середніми зондами 2 і 3. Природно, що ця різниця потенціалів є функцією сили струму І, питомого опору зразка ρ, відстані s і геометричних розмірів зразка. Знайдемо зв'язок U і I, вважаючи, що зразок можна розглядати як напівпростір: його розміри і відстані від зондів до кордонів зразка набагато більші s, тому лінії струму протікають лише в однієї поверхні зразка — тій, на якій встановлені зонди.

Відомо, що електричне поле постійного струму формально аналогічно електростатичному полю. Скористаємося цим. Напруженість електричного поля, що виникає в зразку при втікані через зонд 1 струму І на відстані r₁ від зонда

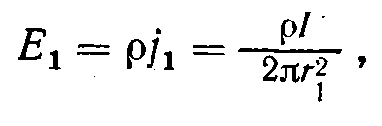
де j₁ - щільність струму. Приймаючи, що при r₁→ ∞ потенціал даного поля , знаходимо по формулі

Аналогічно потенціал φ₄ поля, що виникає при витіканні через зонд 4 струму I на відстані г₄ від нього

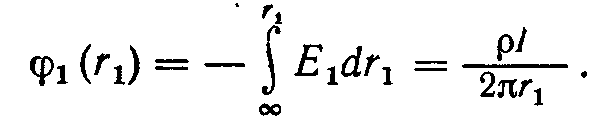
Потенціал крапки, віддалений від зондів 1 і 4 відповідно на відстані r₁ і

r₄, рівний φ₁(r₁)+φ₄(r₄). Враховуючи це, отримуємо, що потенціал зонда 2 U₂= φ₁ (s) + φ₄ (2s), зонда 3 — U₃=φ₁(2s)+ φ₄(s). Різниця потенціалів між ними

звідки по U і І визначається питомий опір ρ.

Вимір різниці потенціалів U в чотирьохзондовому методі проводиться як і в двохзондовому; вплив на результати вимірів неомічності контактів потенційних зондів 2 і 3 такий же.

У зразку кінцевих розмірів хід ліній струму змінюється в порівнянні з випадком напівбезконечного зразка, унаслідок чого змінюється функціональний зв'язок U з І. Проілюструємо це у разі, коли зразок можна розглядати як чверть простору і зонди мають розташування, показане на

рис. 9 суцільними лініями.

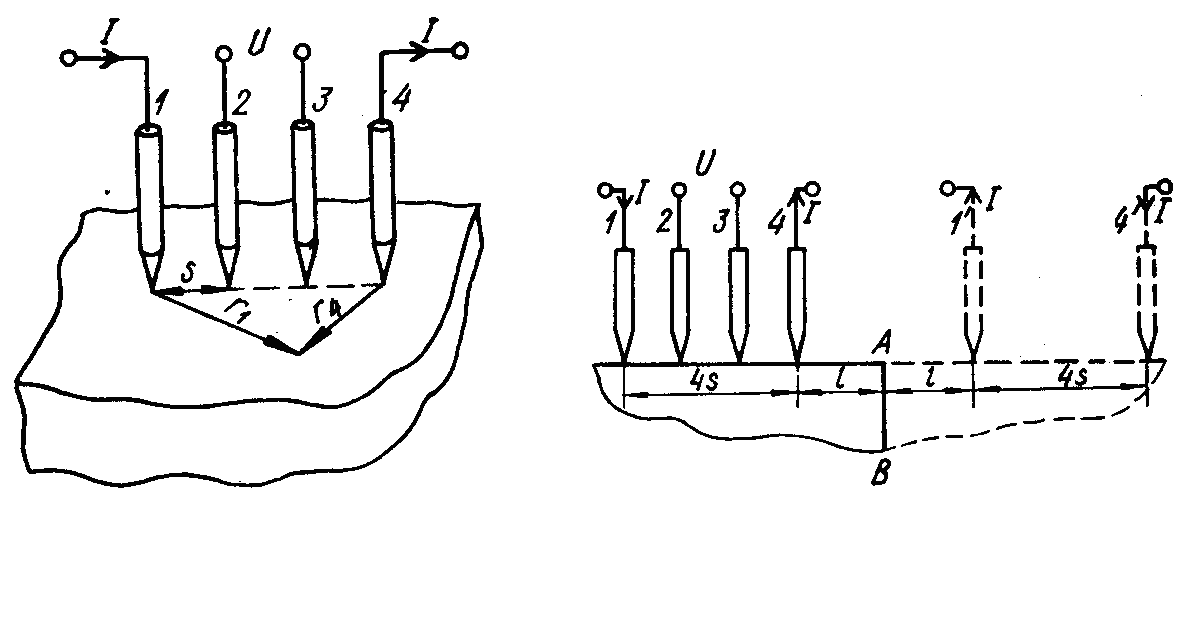
Рис.8.До реалізації чотирьохзондового Рис.9. Зразок у вигляді напівпросто-

методу вимірювання ру з чотирма струмопідвідними

зондами

Тут в порівнянні з випадком рис. 8 додалася вертикальна площина АВ, яка змінює хід ліній струму таким чином, що на ній нормальна складова щільності струму дорівнює нулю. Враховуючи це, неважко зрозуміти, що електричне поле в даному зразку з двома струмопідівідними контактами 1 і 4 таке ж, як і в зображеному на рис. 9 суцільними і штриховими лініями зразку, що представляє напівпростір з чотирма струмопідівідними зондами 1, 4 і 1', 4'. З вираження для потенціалу, створюваного протіканням струму через кожен з цих зондів, після обчислень, подібних виконаним при здобутті формули (3.19), можна показати, що

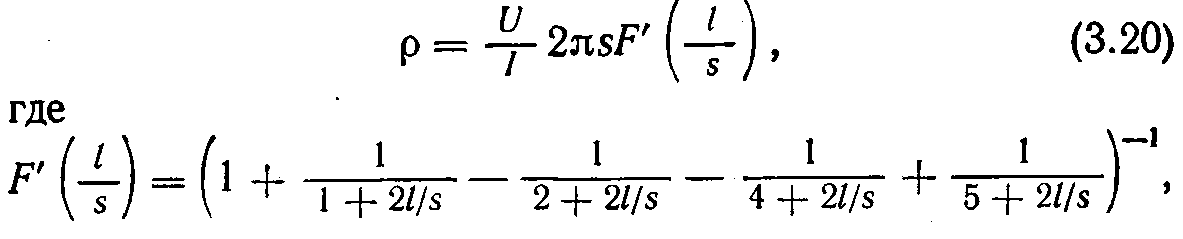
де l - відстань від зонда 4 до вертикальної площини АВ, що обмежує зразок. При s « 2l вираження (3.20) переходить в (3.19).

Чотирьохзондовий метод виміру широко використовується в процесі виробництва напівпровідникових матеріалів і при створенні напівпровідникових приладів. Вирази, зв'язуючі U і І, отримані для найрізноманітніших випадків: зразків у вигляді пластин, пластин з однією поверхнею, покритою металом, брусків і ін. При відстанях від зондів до поверхонь зразка, значно більших s, ці вирази переходять в (3.19) і зразок можна розглядати як напівпростір. Чим менше s, тим для менших зразків справедлива формула (3.19). Це ілюструє рис. 10, де для двох значень s показані розміри зразків (у сантиметрах), при яких обчислення за формулою (3.19), що не враховує їх кінцевості, приводять до погрішності в 1 %.

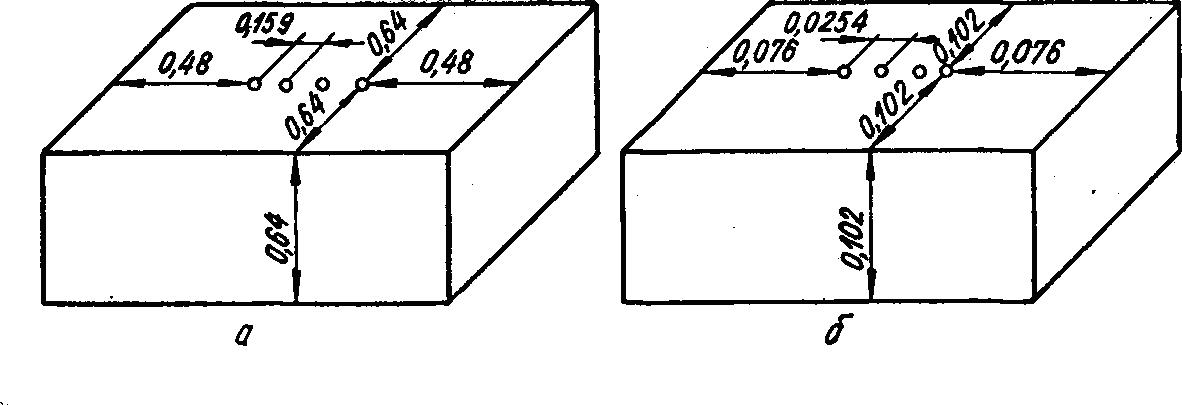
Рис. 10. Зразки різної геометрії

Вимір питомого опору пластин довільної форми. Метод ВАН-дер-ПАУ

При визначенні питомого опору пластин- довільної форми використовується метод Ван-дер-Пау.

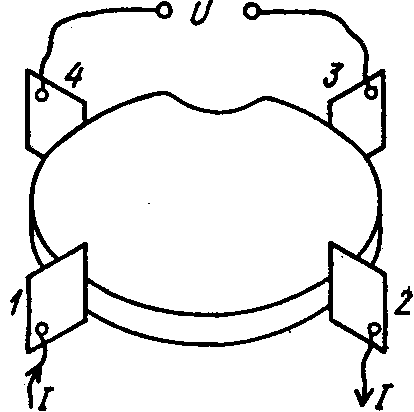
Рис. 11. Схема проведення виміру питомого опору напівпровідника методом

ВАН-дер-ПАУ

У цьому методі на бічній поверхні пластини товщиною d створюються чотири лінійні контакти 1—4 (рис.11). Через контакти 1 і 2 пропускають струм І₁ і вимірюють різницю потенціалів U₁ між контактами 3 і 4. Вимір проводиться за допомогою тих же схем, що і в разі двохзондового і чотирьохзондового методів.

Потім струм I₂ пропускають через контакти 2 і 3 і вимірюють різницю потенціалів U₂ між контактами 1 і 4. Величини R₁=U₁/I₁ і R₂=U₂/I₂ зв'язані між собою співвідношенням

Отримати аналітичне вираження ρ через R₁ і R₂ не удається. Введемо в розгляд величину f за допомогою вираження

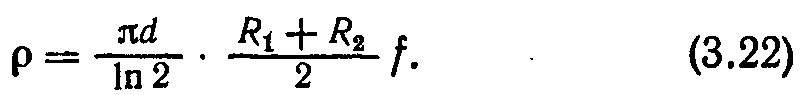
Підставляючи (3.22) в (3.21), отримуємо рівняння

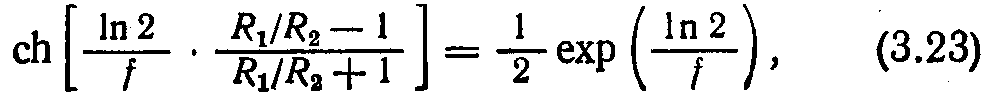
звідки витікає, що f залежить від R1/R2. Отримана з вирішення рівняння (3.23) залежність f від Ri/R2 представлена на рис. 12.

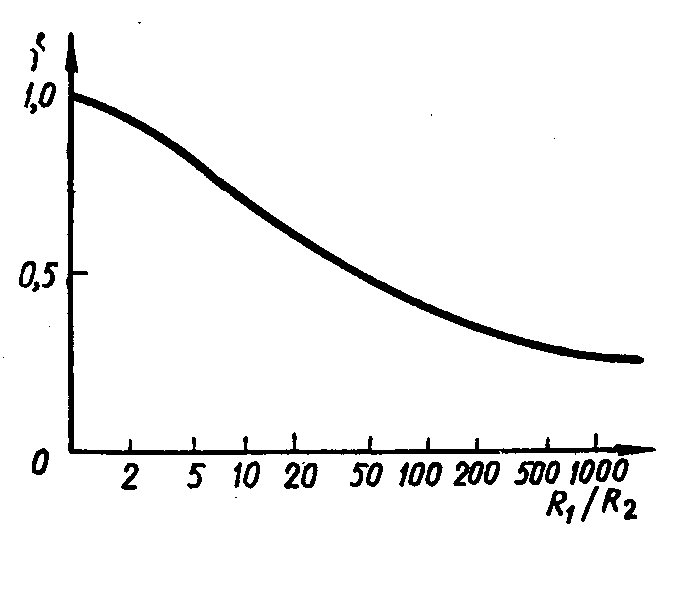
Рис. 12. Залежність f від R1/R2

Використовуючи значення f, що даються нею, по виміряних R1 і R2, можна по формулі (3.22) обчислити питомий опір. При симетричному розташуванні контактів на симетричному зразку, наприклад на крузі або квадраті, R1 = R2 = R і, згідно (3.23), f=1; ρ=(πd/ln 2)·R.

Нерушійні методи вимірювання питомого опору

Описані раніше методи визначення ρ являються рушійними. Це пов'язано з тим, що всі вони використовують електричний контакт зі зразком.

В ряді випадків в метрології напівпровідників віддається перевага так званим безконтактним методам вимірювання ρ, що пов'язано з їх деякими перевагами у порівнянні з зондовими:

1. Не рушійною і незагрязняючою дією на зразок.

2. Можливістю вимірювання зразків з високим перехідним опором контактів.

Правда, слід відмітити, що ці методи програють зондовим у точності.

Є три основні групи безконтактних метода вимірювання ρ:

1)Мостові методи.

2)методи основані на взаємодії напівпровідника з електромагнітним полем коливального контура.

3)НВЧ-методи.

1.Мостові методи. Вони основані на тому, що в одно з плеч мостової схеми, яка живиться змінним струмом високої частоти і має змінний опір R і ємність С, вводиться досліджуваний зразок. Змінюючи значення R і С таким чином, щоб плечі мосту були зрівноважені (тобто досягають відсутності струму, що фіксується стрілкою гальванометра, яка установлюється на позначці 0, і таким чином компенсують міст). При цьому величина R , яка відраховується на шкалі гальванометра, відградуйованого в одиницях R буде пропорційна повному опору зразка. Питомий опір розраховують по формулі:

ρ=(R·S / l), (1)

де S – поперечний переріз зразка; l – довжина зразка; R- повний опір зразка.

2.Методи основані на взаємодії напівпровідника з електромагнітним полем коливального контура. При взаємодії напівпровідника з коливальним контуром LC змінюється добротність цього контуру (Q), яка рівна відношенню його реактивного опору до активного:

Q=1/ R(L/С)^1/2 . (2)

Добротність контура вимірюється за допомогою стандартних приладів – ку метрів в області частот 30-50 МГц. Внесення зразка в контур викликає зміну його добротності ∆Q за рахунок додаткових втрат. Ці втрати пропорційні ρ, тобто ∆Q=f(ρ). Функцію (ρ) будують на основі вимірювання зразків з відомим ρ. Побудувавши градуйовочну криву ∆Q=f(ρ) і визначаючи значення ∆Q, яке вноситься відповідним зразком по градуйовочній кривій визначають його питомий опір.

3.НВЧ – методи. Вони основані на тому, що енергія яка протікає по хвилеводу, попавши на досліджу вальний зразок, частково проходить через нього і частково відбивається . Різниця між потужністю падаючого і потужністю, яка проходить через зразок, НВЧ-випромінення буде пропорційною ρ. Робочий діапазон частот – до 10⁹ Гц.

Тема. 10. Вимірювання концентрації та ступення компенсації домішок у напівпровідниках

Визначення концентрації та рухливості носіїв заряду у напівпровідниках із вимірів ефекту Холла.

Ефект Холу - явище виникнення поперечного електричного полючи в зразку зі струмом, що протікає уздовж його електричним, поміщеному в перпендикулярне до струму магнітне поле.

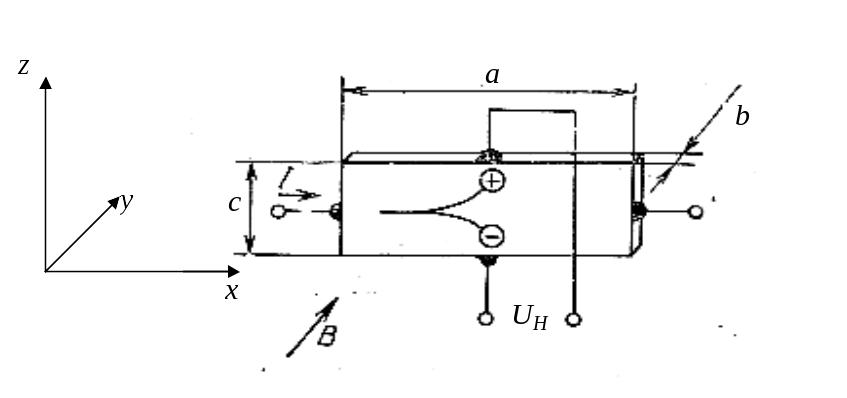
Рис.1. Схема виникнення ефекту Хола.

Нехай напівпровідник має вид паралелепіпеда з розмірами а, b, c (рис.1). Електричне поле Е спрямоване уздовж осі х, у тім же напрямку тече і струм j. Магнітне поле спрямоване уздовж осі y. Електричне поле і струм зв'язані співвідношенням:

(1)

Носії заряду одержують швидкість спрямованого руху (дрейфову швидкість) по полю для дірок і проти полючи для електронів. При включенні магнітного поля на носії заряду діє сила

(2)

При цьому сила Лоренца не залежить від знака носія заряду, тому що при тому самому струмі j електрони і дірки рухаються в протилежних напрямках. У даному випадку носії заряду будуть відхилятися нагору, до верхньої грані, де і буде накопичуватися заряд (позитивний у випадку діркової провідності і негативний у випадку електронної провідності зразка). При цьому виникає дефіцит таких же зарядів на нижній грані зразка. Заряджені грані створюють поперечне стосовно поля Е електричне поле Е_н. Це поле називається полем Холу. У нашому випадку поле Е_н спрямоване нагору в n-зразку і вниз - у p-зразку.

Хол експериментально знайшов, що Е_н визначається щільністю струму j, індукцією магнітного поля В, а також властивостями зразка. Властивості зразка визначаються деякою величиною R, названою коефіцієнтом Холу. При цьому має місце співвідношення:

(3)

Поле Холу повинне компенсувати силу Лоренца, тоді:

(4)

З (4) випливає:

(5)

Тут використана рівність де _d - дрейфова рухливість носіїв заряду.

Згідно (3) можна одержати:

(6)

т.ч. . При цьому  - питома провідність зразка. Порівнюючи (6) і (5), одержуємо:

і

(7) (8)

так як .

У даному випадку через n позначена концентрація носіїв заряду (електронів і дірок). Таким чином, коефіцієнт Холу обернено пропорційний концентрації носіїв заряду (для електронів e<0, для дірок e>0).

Визначивши знак R_н, можна тим самим визначити тип провідності зразка. Знак R визначається за знаком Е_н чи U_н, де U_н потенціал Холу, що зв'язаний з Е_н співвідношенням:

(9)

У зразку зі змішаною провідністю коефіцієнт Холу залежить від концентрації електронів і дірок, а також їхньої рухливості.

Приведений елементарний висновок формули для коефіцієнта Холу не точний. У ньому не врахована різниця між дійсною швидкістю електрона, що входить у вираження сили Лоренца і дрейфовою швидкістю; не враховується розподіл електронів по швидкостях, а також механізми розсіювання. Правильне вираження має вид:

(10)

де - хол-фактор,  - час релаксації. Кутові дужки означають усереднення: ² - середній квадрат, а ² - квадрат середнього. Можна показати, що:

(11)

Це значить, що r_н1, при В . Звідси випливає, що для визначення фактору Холу необхідно виміряти R_н при даному значенні В і при дуже великому В (сильне поле). Тоді r_н(В)= R_н(В)/ . Практично дуже великому В повинна відповідати нерівність В1, слабкому полю відповідає нерівність В1.

Величина r_н залежить від механізму розсіювання носіїв заряду. Для з'єднань з великою рухливістю носіїв заряду умова B виконується при не дуже великих значеннях В.

Тому що для прямокутного зразка I=jbc, a U_н=Е_нз, те з (6) випливає:

.

(12)

Звідси одержуємо:

.

(13)

Тому що  = еn, то повинна виконуватися рівність  =. Оскільки реальне значення R_н відрізняється від , то

Rн=н,

(14)

де _н так звана холівська рухливість носіїв заряду. З закону Ома маємо I=Ebc чи I=bcU_/a, де U_=Ea - напруга, прикладена до кінців зразка. Використовуючи цю рівність, а так само і (14), одержуємо:

.

(15)

Формули (10), (13) і (15) є основними для виконання роботи. За допомогою (13) знаходимо R_н, по формулі (10) визначаємо холівську рухливість. Питому провідність визначаємо за допомогою формули (див. текст):

(16)

Методи вимірювання ступення компенсації домішок у напівпровідниках.

1. Метод Буша - Вінклера

Він заклечається в дослідженні температурної залежності концентрації носіїв заряду, визначенної по результатам холовських вимірювань. Мета такого аналізу – визначення концентрації домішки, яка знаходиться в напівпровіднику, енергії її іонізації, а також сорту домішки. Компенсація визначається якісно по нахилу температурної залежності.

2.Метод Вінецького.

Цей метод розроблено для германію. Як відомо, температурна залежність рухомості в області решіт очного розсіювання визначається в германії наступним чином:

μ_{n ~T}^-3/2;

μ_{p ~T}^-5/2.

Для любої фіксованої температури можна побудувати теоретичні криві залежності lg(ρ/ρ_L) від lg(N_d+ N_a), де ρ – виміряне, а ρ_L – теоретичне значення питомого опору.

Вимірюючи ρ при цих фіксованих температурах, знаходять сумарну концентрацію іонізованих домішок N_і = N_d+ N_a, що в сумі з результатами вимірювань ефекта Холла ( n = N_d+ N_a) дає можливість визначити роздільно N_d і N_a.

Недолік методу: невеликий концентраційний діапазон –

від 10¹³ до 10¹⁵ см^-3.

Методи визначення концентрації електрично пасивних домішок у напівпровідниках.

Оптичний метод. Методика визначення концентрації пасивної домішки – кисло роду заклечається в вимірювані ІК – поглинання з допомогою стандартних спектрофотометрів з послідуючим підрахунком піка поглинання і його перерахунком в концентрацію кислороду.

Є ще декілька методів визначення концентрації електрично пасивних домішок у напівпровідниках: мас-спектроскопічні методи; радіоактивний і нейтронно-активаційний аналізи, метод «помічених» атомів і ін.

Системи критеріїв оцінки якості напівпровідникових матеріалів і структур на основі визначенних параметрів.

Представлення про кристали високої якості основується на одночасному досягненю значень електричних параметрів, ступеня структурної досконалості, геометричних розмірів і форми.

Таким чином, система критеріїв оцінки якості напівпровідникових матеріалів і структур включає в себе електрофізичні, структурні, геометричні параметри і може бути принята лише в якості базової, яка забезпечує перше приближення до деякої системи, яка обладає абсолютною повнотою.

РЕКОМЕНДОВАНА ЛІТЕРАТУРА

а) Основна

1. Головко Д.Б., Рего К.Г., Скрипник Ю.О. Основи метрології та вимірювань. –

К.: Либідь, 2001.-408с.

2. Поліщук Є.С., Дорожовець М.М., Івахів О.В. та ін. Засоби та методи

вимірювань неелектричних величин. –Львів: Видавництво «Бескид Біт»,

2008.-618с.

3. Цацюра С.В., Цацюра В.Д. Метрологія, основи вимірювань. Стандартизація

та сертифікація. - К.: Знання, 2005.-242с.

4. Поліщук Є.С. Метрологія та вимірювальна техніка. –Львів: Видавництво

«Бескид Біт», 2003. - 544с.

5.Маркин Н.С.. Ершов В.С. Метрология. Введение в специальность. –М.:

Издательство стандартов, 1991. – 208с.6. Мейзда Ф. Электронные

измерительные приборы и методы измерений.-М: Мир,1990.-535с.

7. Рего К. Г. Метрологическая обработка результатов технических

измерений: Справочное пособие. – К.: Техника, 1987.