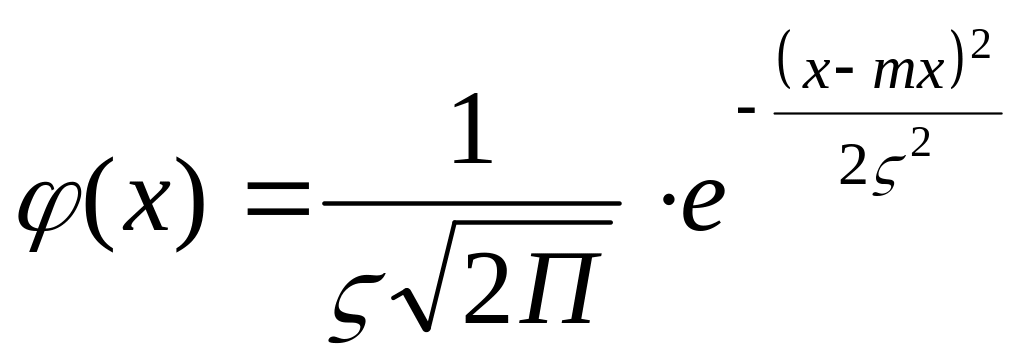Змістовний модуль №3. Методи та засоби вимірювань параметрів напівпровідникових матеріалів та структур

Тема 7. Метрологічне забезпечення вимірювань параметрів напівпровідників (лекції №24-28)

Основні поняття теорії випадкових похибок

Нормальний закон розподілу випадкової величини. Методи перевірки нормативності розподілу випадкових похибок.

При вивченні випадкових похибок за допомогою теорії ймовірності і математичної статистики найчастіше використовують закон нормального розподілу випадкових величин:

, (1)

де m_x – математичне сподівання випадкової величини Х; ς – середньоквадратичне відхилення випадкової величини; ς ² = Д – дисперсія випадкової величини.

Закон нормального розподілу випадкових величин, що виражається формулою (1), дає можливість обчислити імовірність перебування випадкової величини Х в визначених границях ( тобто від - ς до + ς ).

Строго говорячи, нормальний закон розподілу може точно описувати тільки нескінченну сукупність випадкових погрішностей (її називають генеральної). Однак його можна застосовувати і для опису кінцевих сукупностей, вважаючи, що вони випадково обрані з генеральної (саме тому кінцеві сукупності називаються вибірками).

У вибірках з кінцевим числом вимірів n точне обчислення m_x і ς неможливо; замість них приблизно обчислюють їхні статистичні оцінки та Для вибірки з n значень оцінкою математичного чекання випадкової величини (її найбільш ймовірним значенням) є

(2)

тобто приймаємо, що математичний опис дорівнює середньоарифметичному значенню випадкової величини .

Вибіркове середньоквадратичне відхилення окремих результатів спостережень (вимірів) для тієї ж вибірки можна обчислити по формулі Бесселя:

(3)

де х_i – x – випадкове відхилення і-го результату спостережень від знайденого значення .

Формула Бесселя справедлива для будь-якого закону розподілу випадкових похибок. При нормальному розподілі похибок можна обчислити S по спрощеній формулі Петерса:

(4)

Якщо значення S_п істотне відрізняється від S, отриманого по формулі Бесселя (3), то можна вважати, що в даній вибірці дійсний закон розподілу похибок відрізняється від нормального і це вибірку обробляти за правилами для випадкових похибок не випливає.

Оцінка математичного опису випадкової величини для вибірки небагато відрізняється від (що обчислюється для нескінченно великої сукупності випадкових похибок). Якщо закон розподілу похибок нормальний можна вважати, що відхилення від не перевищує

(5)

де S - середньоквадратичне відхилення значення (від математичного чекання ).

Надійні границі, у яких при заданій імовірності знаходяться величина Х, обчислюється по формулі: (для нижньої границі) і (для верхньої), де - коефіцієнт надійності для імовірності Р. Для невеликих вибірок (n<30) надійні границі залежать також і від кількості вимірів (спостережень) n (це уточнення запропонував Стьюдент):

Таблиця 1. Коефіцієнт Стьюдента

n	РД
	0,80	0,90	0,95	0,99	0,995	0,999
2 3 4 5 6 7 8 9 10 12 14 16 18 20 30 40 50 60 ∞	3,080 1,886 1,638 1,533 1,476 1,440 1,415 1,397 1,383 1,363 1,350 1,341 1,333 1,328 1,316 1,306 1,298 1,290 1,282	6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,80 1,77 1,75 1,74 1,73 1,70 1,68 1,68 1,67 1,64	12,71 4,30 3,188 2,77 2,57 2,45 2,36 2,31 2,26 2,20 2,16 2,13 2,11 2,09 2,04 2,02 2,01 2,00 1,96	63,70 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,11 3,01 2,95 2,90 2,86 2,75 2,70 2,68 2,66 2,58	127,30 14,10 7,50 5,60 4,77 4,32 4,03 3,83 3,69 3,50 3,37 3,29 3,22 3,17 3,20 3,12 3,09 3,06 2,81	637,20 31,60 12,94 8,61 6,86 9,96 5,40 5,04 4,78 4,49 4,22 4,07 3,96 3,88 3,65 3,55 3,50 3,46 3,29

У технічних вимірах (як лабораторних, так і виробничих) обчислення виконуються з імовірністю Р=95%; в окремих випадках, коли експеримент неможливо повторити, приймають Р=99%. Тільки, в особливо важливих випадках, якщо результати експерименту впливають на життя і здоров'я людей, варто брати Р=99%.

Оскільки методи обробки результатів вимірів базуються на використанні нормального закону розподілу, перед початком обчислень бажано переконається в тім, що дана сукупність відповідають нормальному закону розподілу.

В останні роки для порівняно невеликих сукупностей вимірів (3<n<40) таку перевірку часто здійснюють графічним методом. У цьому випадку для даної вибірки за визначеними правилами коштують графік емпіричного розподілу і якщо крапки цього графіка розташовуються приблизно на прямої лінії, те дана сукупність відповідає нормальному закону розподілу.

Застосовуючи графоаналітичний метод аналізу, випливає насамперед упорядкувати вибірку, розмістити значення вимірів Х_і в порядку зростання:

X₁ X₂ …... X_n

Якщо деякі значення в такому варіаційному ряді повторюються, то в робочу таблицю їх записують тільки раз, але вказують кількість цих значень (частота m_і даного варіанта Х_і ряду) У наступній графі записують значення так називаної частоти М_і (сумарна кількість значень m_і від початку до Х_і включно плюс попереднє значення М_і).

Після цього розраховують інтеграл Лапласа:

(6)

де n – кількість вимірів, кількість значень Х_і (кількість членів вибірки).

Потім за знайденим значенням інтеграла Лапласа по таблиці “Значення інтеграла Лапласа” (таблиці маються в довідковій літературі) знаходять значення аргументу і далі будують графіка . Якщо графік функції приблизно прямолінійний, то можна вважати, що вибірка не суперечить нормальному закону розподілу.

Одержання найбільш достовірного результату виміру й оцінка його погрішності – основна мета обробки даних, отриманих у ході експерименту. Вибір методу обробки залежить від числа експериментальних даних (багаторазові, однократні виміри), виду вимірів, виду розподілу погрішностей вимірів.

Для оцінки результату однократного виміру використовують результати спеціального поставленого чи експерименту дані попередніх досліджень умов вимірів, погрішності використання засобів і методів вимірів, суб'єктивних погрішностей.

При визначенні результату багаторазових вимірів звичайно використовуються ймовірні методи оцінки, що розглянуті вище. Найбільше поширення одержали статистичні методи обробки (при цьому розподіл отриманого ряду експериментальних даних не суперечать нормальному розподілу).

У загальному алгоритм обробки результатів багаторазових вимірів може побут представлений у наступному виді:

1. Одержавши експериментальні дані у виді статистичного ряду (вибірки), аналізують і виключають з результатів вимірів систематичні помилки (див. лекцію «Виключення систематичних погрішностей»).

2. Перевіряють, чи відповідає вибірка нормальному закону розподілу. Відкидають промахи. (див. лекцію «Методи перевірки нормального розподілу випадкових похибок»).

3. Аналізують вибірку (статистичний ряд) з метою виявлення грубих помилок і промахів: установлюють при використанні довірчого інтервалу різко виділяються виміри Х_max, X_min.

При наявності грубих помилок, критерії їхньої появи обчислюються по формулах:

(7)

(8)

де Х_max, Х_min найбільше і найменше значення з n вимірів, - середньоквадратичне відхилення результату вимірів.

У таблиці 2 приведені залежності від довірчої імовірності максимальні значення β_max, що виникають унаслідок статистичного розкиду.

Якщо, розраховане по формулі (7), значення β₁>β_max, те значення Х_max необхідно виключити зі статичного ряду як грубу погрішність. Якщо, розраховане по формулі (8), значення β₂<β_max виключається величина X_min.

Таблиця 2. Критерій появи грубих помилок

n	βmax при рд			n	βmax при рд
	0,90	0,95	0,99		0,90	0,95	0,99
3 4 5 6 7 8 9 10 11 12 13 14	1,41 1,64 1,79 1,89 1,97 2,04 2,10 2,15 2,19 2,23 2,26 2,30	1,41 1,69 1,87 2,00 2,09 2,17 2,24 2,29 2,34 2,39 2,43 2,46	1,41 1,72 1,96 2,13 2,26 2,37 2,46 2,54 2,61 2,66 2,71 2,76	15 16 17 18 19 20 25 30 35 40 45 50	2,33 2,35 2,38 2,40 2,43 2,45 2,54 2,61 2,67 2,72 2,76 2,80	2,49 2,52 2,55 2,58 2,60 2,62 2,72 2,79 2,85 2,90 2,95 2,99	2,80 2,84 2,87 2,90 2,93 2,96 3,07 3,16 3,22 3,28 3,33 3,37

4. Після виключення грубих помилок обчислюють середньоквадратичне і середньоквадратичне відхилення очищеного ряду по формулах (2) і (3)

5. Знаходять середньоарифметичне значення середньоквадратичне відхилення ς₀ серії вимірів і коефіцієнт варіації, відповідно по формулах:

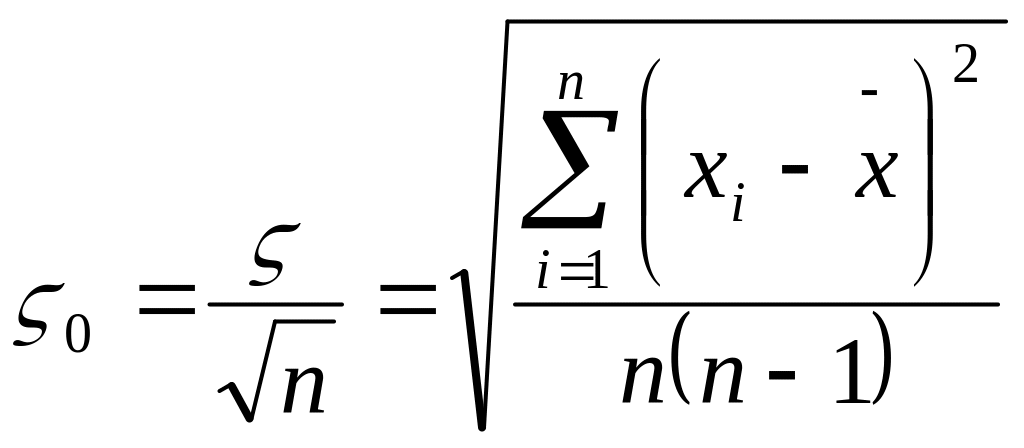(9)

(10)

Коефіцієнт варіації характеризує мінливість. Чим вище , тим більше мінливість вимірів щодо середніх значень. оцінює також при оцінці декількох вибірок.

6. При великій вибірці задаються довірчою імовірністю Р_д=Ф(t) чи рівнянням значимості (1-рд) і по таблиці і по приведеній нижче інтегральній функції Лапласа визначають t.

Таблиця 3. Інтегральна функція Лапласа

t	Pд	t	Pд	t	Pд
0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70	0,0000 0,0399 0,0797 0,1192 0,1585 0,1974 0,2357 0,2737 0,3108 0,3473 0,3829 0,4177 0,4515 0,4843 0,5161	0,75 0,80 0,85 0,90 0,95 1,00 1,05 1,10 1,15 1,20 1,25 1,30 1,35 1,40 1,45	0,5467 0,5763 0,6047 0,6319 0,6579 0,6827 0,7063 0,7287 0,7419 0,7699 0,7887 0,8064 0,8230 0,8385 0,8529	1,50 1,55 1,60 1,65 1,70 1,75 1,80 1,85 1,90 1,95 2,00 2,25 2,50 3,00 4,00	0,8664 0,8789 0,8904 0,9011 0,9109 0,9199 0,9281 0,9357 0,9426 0,9488 0,9545 0,9756 0,9876 0,9973 0,9999

7. При малій вибірці (n 30) у залежності від прийнятої довірчої імовірності Р_д і числа членів ряду n визначають коефіцієнт Стьюдента t_cт; розраховують довірчий інтервал за допомогою формули (11) для великої чи вибірки формули:

(12)

для малої вибірки (де - середньоквадратичне значення середньоквадратичного відхилення серії вимірів, обумовлене вираженням (9); t_ст – коеф. Стьюдента обумовлений по таблиці 1; - довірчий інтервал для малої вибірки).

8. По формулі:

(13)

установлюють щире (дійсне) значення досліджуваної величини.

9. Оцінюють відносну погрішність (%) результатів серії вимірів при заданій довірчій імовірності Р_д:

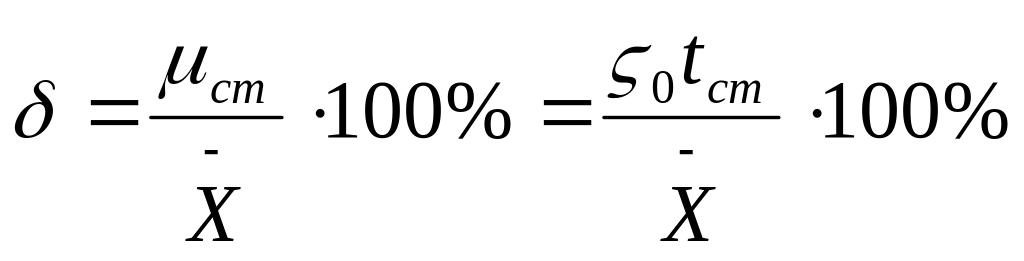(14)

Якщо погрішність серії вимірів порівнянна з погрішністю приладу B_пр, то границі довірчого інтервалу варто визначати по формулі:

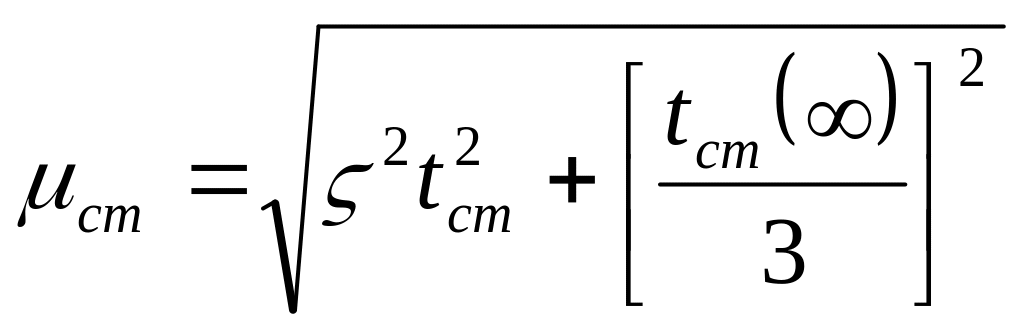(15)

Формулою (15) варто користатися при t_ст 3в_пр. Якщо ж t_ст 3в_пр, то довірчий інтервал обчислюють за допомогою формули (12):

,

тут В_пр= , (16)

де - показання приладу; - дійсне значення вимірюваної величини, установлене за допомогою зразкового вимірювального приладу.

У дослідженнях часто по заданій точності (%) і довірчої імовірності виміру визначають кількість вимірів, що гарантують необхідні значення і Р_д (Примітка: значком позначають помилку виміру, що те саме).

Точність виміру визначається по формулі: . (17)

Довірчий інтервал помилок виміру визначається по формулі:

. (18)

Мінімальна кількість вимірів N_min, необхідне для гарантування необхідних значень і Р_д визначаються по формулі:

, (19)

де - коефіцієнт варіації (мінливості), %; - точність виміру (помилка виміру), %; t – гарантійний коефіцієнт (для великої вибірки при n>30 є аргументом функції Лапласа і визначаються по таблиці 3. (При n<30 – аргументом функції Стьюдента t_cт (табл.1).

Основні положення метрології напівпровідників

Основу виробів напівпровідникової електроніки складають напівпровідникові матеріали і структури. Основні напівпровідникові матеріали – це кремній, арсенід галій, фосфід індія, германій, тройні та четверні тверді розчини А³В⁵ та ін. Спеціальна область метрології, яка займається питаннями забезпечення єдності вимірювань і одно направленістю засобів вимірювання по відношенню до напівпровідникових кристалів та структур. називається метрологією напівпровідників.

Практична метрологія напівпровідників вивчає:

1.Системи фізичних критеріїв оцінки якості напівпровідникових матеріалів і структур.

2. Фізико-хімічні методи аналізу мікро домішок у напівпровідниках.

3. Методи і апаратуру вимірювання питомого електричного опору напівпровідникових матеріалів і структур.

4. Методи визначення концентрації домішок у напівпровідниках і параметрів нерівно вісних носіїв заряду.

5. Методи і апаратуру контролю ступенню структурної досконалості напівпровідників.

6. Методи і апаратуру для виробничого контролю епітаксій них шарів напівпровідникових структур.

7. Фізичні методи контролю технології виробництва напівпровідникових приладів і мікросхем.

Основними характеристиками напівпровідникових матеріалів і структур є: питомий електричний опір, час життя нерівновісних носіїв

заряду, концентрація домішок, дифузійна довжина нерівновісних носіїв

заряду.