6. Энергия электрического поля

Основные формулы

• Энергия заряженного конденсатора

. (6.1)

• Объемная плотность энергии электрического поля

, (6.2)

где – напряженность электрического поля, – электрическое смещение.

Примеры решения задач

Задача 1. На плоский воздушный конденсатор подается разность потенциалов кВ. Площадь каждой пластины , расстояние между ними см. После зарядки конденсатор отключают от источника и затем раздвигают его обкладки так, что расстояние между ними увеличивается вдвое. Определите: a) работу по раздвижению обкладок; б) плотность энергии электрического поля до и после раздвижения обкладок.

Решение.

Работа по раздвижению пластин равна изменению энергии заряженного конденсатора:

. (1)

Энергия заряженного конденсатора определяется соотношением:

,

тогда , . (2)

После отключения конденсатора от источника заряд на его обкладках не изменяется: (3)

так как , , то на основании соотношения (3) имеем:

, откуда . (4)

Емкость плоского конденсатора до и после раздвижения обкладок будет

и . (5)

Подставим соотношения (5) в выражение (4) и учтем, что , получим

. (6)

Тогда работа будет:

. (7)

Плотность энергии рассчитывается по формуле

.

Плотность энергии до раздвижения пластин , (8)

после раздвижения обкладок , (9)

где ; .

Учитывая, что и , получаем:

, (10)

следовательно, плотность энергии не меняется.

Переведем физические величины в систему СИ: В, м², м.

Произведя вычисления, получим:

мДж; .

Задача 2. Слюдяная пластинка заполняет все пространство между обкладками плоского конденсатора емкостью мкФ. Диэлектрическая проницаемость слюды заряд конденсатора мкКл. Какую работу надо совершить, чтобы вынуть пластинку из конденсатора?

Решение.

Работа будет равна изменению потенциальной энергии конденсатора, взятому со знаком «минус»:

. (1)

Потенциальная энергия конденсатора с пластинкой: , (2)

без пластинки: 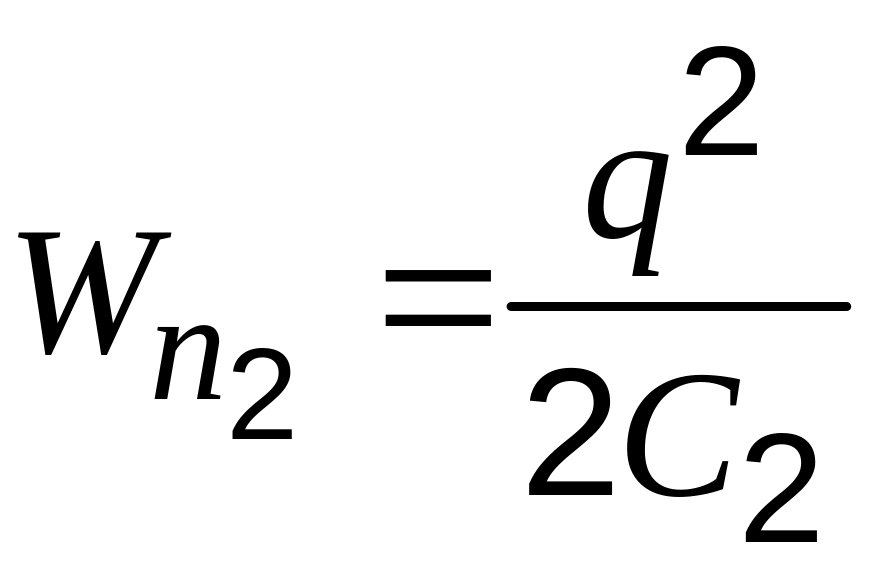. (3)

Емкость плоского конденсатора определяется выражением

, , (4)

тогда , (5)

следовательно,

.

Переведем все величины в систему СИ:

, .

Произведем вычисления:

.

Знак «минус» означает, что энергия поля конденсатора уменьшилась.

Задача 3.

Внутри горизонтально расположенного плоского конденсатора с площадью обкладок и расстоянием между ними находится пластина из стекла, целиком заполняющая пространство между обкладками конденсатора. Какую работу необходимо совершить, чтобы удалить пластинку? Конденсатор подсоединен к батарее с эдс В. Диэлектрическая проницаемость стекла . Силами трения пренебречь (рис. 6.1).

а б

Рис. 6.1

Решение.

Электрическое поле между обкладками конденсатора поляризует диэлектрик и втягивает его в область более сильного поля. Поэтому сила , которая вытаскивает пластинку, будет изменяться. Работу этой силы можно найти из закона сохранения энергии: изменение энергии конденсатора равно сумме работ, совершаемых всеми силами, действующими в данной системе.

,

где – работа силы ; – работа силы тяжести; – работа силы реакции; – работа сторонних сил источник тока.

и , так как силы и перпендикулярны перемещению.

Работа сторонних сил:

,

где – изменение заряда конденсатора (заряд, протекающий через источник), ,

– заряд на обкладках конденсатора с диэлектриком;

– заряд на обкладках конденсатора без диэлектрика.

Следовательно,

Энергия заряженного конденсатора определяется по формуле ,

так как конденсатор не отключается от источника, то разность потенциалов между его обкладками остается постоянной, равной эдс батареи: .

Энергия конденсатора с диэлектриком:

, где – емкость конденсатора с диэлектриком.

Энергия конденсатора без диэлектрика:

, где – емкость конденсатора в отсутствии диэлектрика.

Следовательно,

;

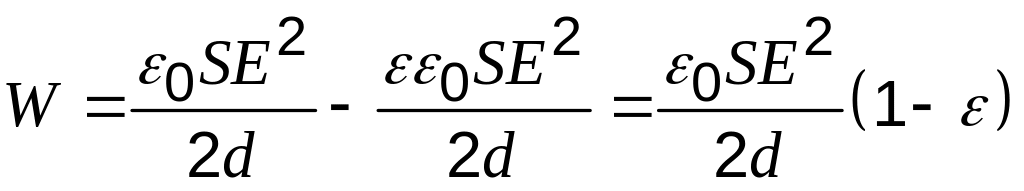Выразим величину в системе СИ:

, .

В результате вычислений получаем .

Задача 4. Четыре одинаковых шарика с одинаковыми одноименными зарядами (рис. 6.2) связаны одинаковыми нерастяжимыми нитями. Докажите, что равновесие достигается, когда шарики располагаются в вершинах квадрата. На шарики действуют только кулоновские силы и силы натяжения нитей.

Решение.

Шарики будут отталкиваться друг от друга, так как они имеют одноименные заряды. Поэтому все четыре нити натянуты и, следовательно, при равновесии шарики располагаются в вершинах ромба. Обозначим угол между стороной ромба и большой диагональю (рис. 6.2).

Тогда длины диагоналей будут:

, ,

где – сторона ромба.

Шарики будут находиться в положении устойчивого равновесия, если потенциальная энергия кулоновского взаимодействия шариков минимальна. Так как расстояния между соседними шариками не меняются (длина нити ), то достаточно рассмотреть энергию взаимодействия шариков на одной диагонали, т. е.

,

где .

Для определения минимального значения потенциальной энергии находим производную и приравниваем ее к нулю:

,

откуда следует:

, значит, убывает при изменении угла от до и возрастает при изменении угла от до . Минимальное значение достигается при , когда ромб превращается в квадрат.

Задача 5. Плоский воздушный конденсатор, расстояние, между вертикальными обкладками которого равно , заряженный до напряжения , расположен так, что обкладки касаются жидкого диэлектрика, находящегося в широком сосуде. Определите высоту поднятия жидкости в пространстве между обкладками, если ее плотность равна , диэлектрическая проницаемость равна , а высота обкладок – (рис. 6.3).

Решение.

Систему «конденсатор – жидкость, поднявшаяся между его обкладками – гравитационное поле Земли» можно считать, замкнутой, если пренебречь силами вязкого трения и силами поверхностного натяжения. Такая система может быть описана законом сохранения энергии.

Н улевой уровень потенциальной энергии в гравитационном поле Земли выберем на горизонтали, расположенной на уровне поверхности жидкости в сосуде. Перед касанием обкладок и жидкости потенциальная энергия системы равна энергии воздушного конденсатора ,

где – электроемкость воздушного конденсатора;

– заряд конденсатора в начальный момент времени.

Следовательно,

.

После касания обкладок жидкости, она поляризуется и втягивается в пространство между обкладками. Так как заряд на пластинах конденсатора не меняется (источник отключен), а емкость увеличивается (после поднятия жидкости на высоту конденсатор превращается в два конденсатора, соединенных параллельно), то энергия поля уменьшается. Это уменьшение компенсируется увеличением потенциальной энергии столба жидкости между обкладками.

Энергия системы после поднятия жидкости на высоту будет:

,

где – энергия заряженного конденсатора; – потенциальная энергия столба жидкости (учли, что центр масс части жидкости , втянутой между пластинами, оказался на высоте ),

,

.

Емкость системы можно найти как сумму двух электроемкостей: – электроемкость между частью пластин, находящейся в воздухе, и – электроемкость той части пластин, которая находится в жидкости

; ,

тогда .

По закону сохранения энергии:

или , откуда .

Подставим в полученные уравнения значения заряда , емкостей и и массы , получаем уравнение:

,

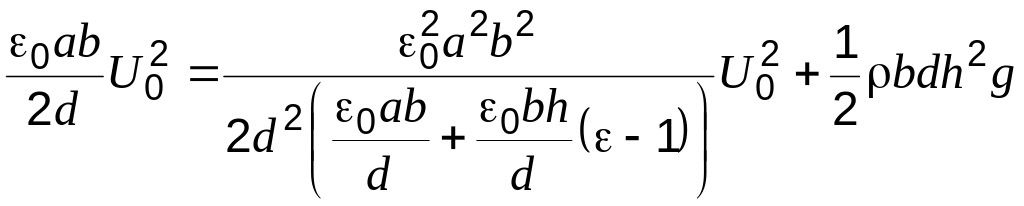после математических преобразований получаем:

,

отсюда искомая высота поднятия жидкости

.

Задача 6. Сплошной эбонитовый шар радиусом см заряжен равномерно с объемной плотностью . Определите энергию электростатического поля, заключенную внутри шара.

Решение.

Выберем элемент объема шара. Энергия такого элементарного объема будет: ,

где – объемная плотность энергии, ; – напряженность электрического поля, ; – электрическое смещение.

Следовательно, .

Объем шара определяется формулой , тогда элемент объема .

По теореме Остроградского-Гаусса

, откуда ,

тогда , .

Следовательно, .

Полная энергия, заключенная внутри шара, определяется интегрированием

.

Переведем физические величины в систему СИ:

, .

Произведя вычисления, получаем .

Задачи для самостоятельного решения

1. Разность потенциалов кВ на батарее из пяти последовательно соединенных конденсаторов емкостью каждой поддерживают постоянной. При этом один из конденсаторов пробивается. Определите: а) изменение энергии батареи; б) работу разряда; в) работу источника напряжения.

2. Два конденсатора, емкости которых и , соединены последовательно. Батарею заряжают до разности потенциалов . Затем конденсаторы, не разряжая, соединяют параллельно. Определите работу разряда, происходящего при этом переключении.

3. Обкладки заряженного плоского конденсатора площадью 100 см² каждая притягиваются друг к другу с силой 4 мН. Определите плотность энергии электростатического поля конденсатора, если его заряд равен ?

4. Шар радиусом 10 см, заряженный до потенциала 2,7 кВ, соединили длинным тонким проводником с незаряженным шаром радиусом 5 см. Какое количество теплоты выделилось при этом в соединительном проводнике, если его сопротивление 10 Ом?

5. Расстояние между обкладками плоского конденсатора уменьшили в 3 раза, предварительно отключив его от источника напряжения. Во сколько раз изменились при этом энергия поля конденсатора и объёмная плотность энергии? Во сколько раз изменятся эти величины, если конденсатор при сближении обкладок не отключать от источника напряжения.

6. Один заряженный проводник обладает энергией 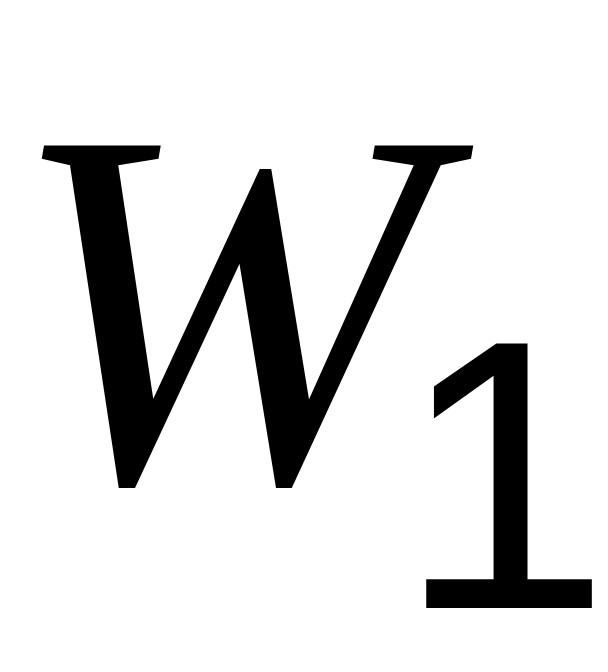, а второй – . Какое количество теплоты выделится, если их соединить проводником, емкостью которого можно пренебречь? Емкости проводников одинаковы.

7. Заряженный воздушный конденсатор с напряжением на обкладках отключили от источника напряжения, после чего между его обкладками поместили диэлектрик с относительной диэлектрической проницаемостью 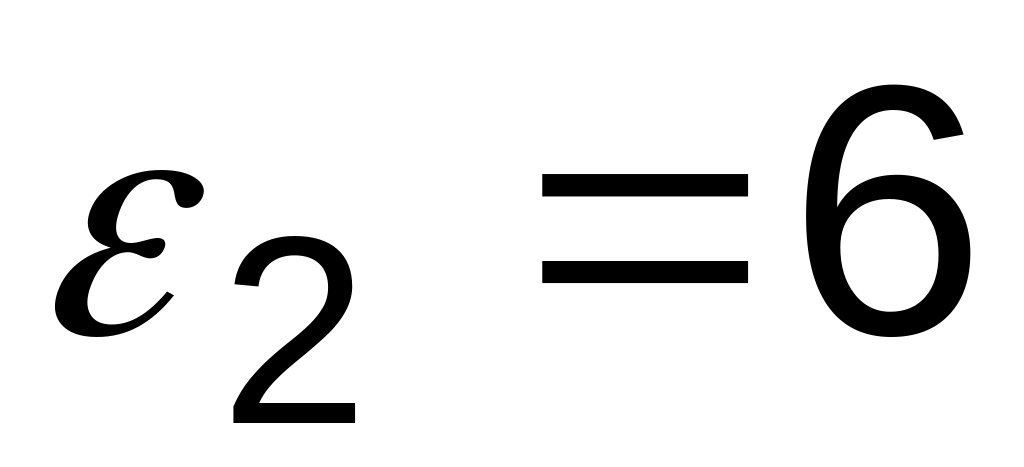, в результате чего напряжение на обкладках увеличилось вдвое. Найти изменение объемной плотности электрической энергии поля конденсатора. Расстояние между обкладками конденсатора мм.

8. Уединенная металлическая сфера электроемкостью заряжена до потенциала . Определите энергию поля, заключенную в сферическом слое между сферой и концентрической с ней сферической поверхностью, радиус которой в раз больше радиуса уединенной сферы.

9. Плоский конденсатор переменной емкости, площадь пластин которого 200 см², заряжен до разности потенциалов . Затем одну из пластин конденсатора сдвинули так, что при неизменном расстоянии между пластинами емкость конденсатора уменьшилась в раза. Определите работу, затраченную на смещение пластины, если расстояние между пластинами , а уменьшение емкости происходило без отключения конденсатора от источника.

10. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом каждая. Расстояние между пластинами равно 1 см. Конденсатор зарядили до разности потенциалов 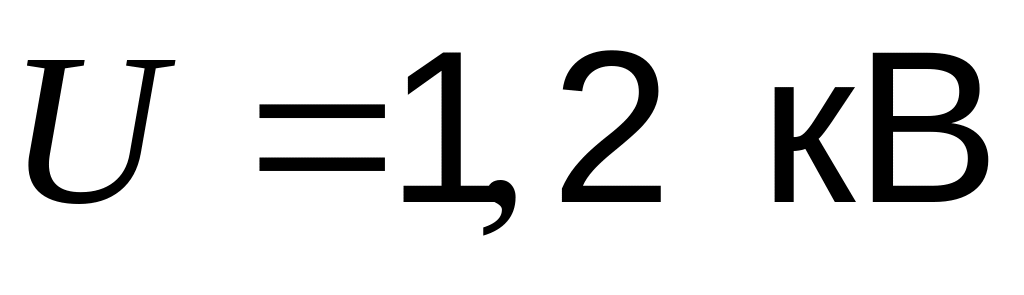и отключили от источника тока. Какую работу нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до ?

11. Два одинаковых воздушных конденсатора емкостью каждый заряжены до разности потенциалов . Один из конденсаторов погружают в заряженном состоянии в керосин, после чего конденсаторы соединяют параллельно. Определите работу происходящего при этом разряда.

12. Между пластинами плоского конденсатора площадью находится металлическая пластинка такой же площади. Расстояние между обкладками конденсатора см, толщина пластинки см. Какую работу нужно совершить, чтобы извлечь эту пластинку из конденсатора, если он подключен к источнику, дающему напряжение В?

13. Конденсатор электроемкостью зарядили до разности потенциалов кВ и отключили от источника. Затем к конденсатору присоединили параллельно второй, незаряженный конденсатор электроемкостью пФ. Определить энергию, израсходованную на образование искры, проскочившей при соединении конденсаторов.

14. Пространство между пластинами плоского конденсатора заполнено диэлектриком (фарфор), объем которого равен 100 см³. Поверхностная плотность заряда на пластинах конденсатора равна . Вычислить работу, которую необходимо совершить для того, чтобы удалить диэлектрик из конденсатора. Трением диэлектрика о пластины конденсатора пренебречь.

15. Вычислить энергию электростатического поля металлического шара, которому сообщен заряд 100 нКл, если диаметр шара равен 20 см.

16. Уединенный металлический шар радиусом см несет заряд . Концентрическая этому шару поверхность делит пространство на две части (внутренняя конечная и внешняя бесконечная), так что энергии электрического поля обеих частей одинаковы. Определить радиус этой сферической поверхности.

17. Сплошной парафиновый шар радиусом 10 см заряжен равномерно по объему с объемной плотностью . Определите энергию электрического поля, сосредоточенную в самом шаре, и энергию вне его.

18. Эбонитовый шар равномерно заряжен по объему. Во сколько раз энергия электрического поля вне шара превосходит энергию поля, сосредоточенную внутри шара?

19. Металлический шар радиусом см несет заряд нКл. Шар окружен слоем эбонита толщиной 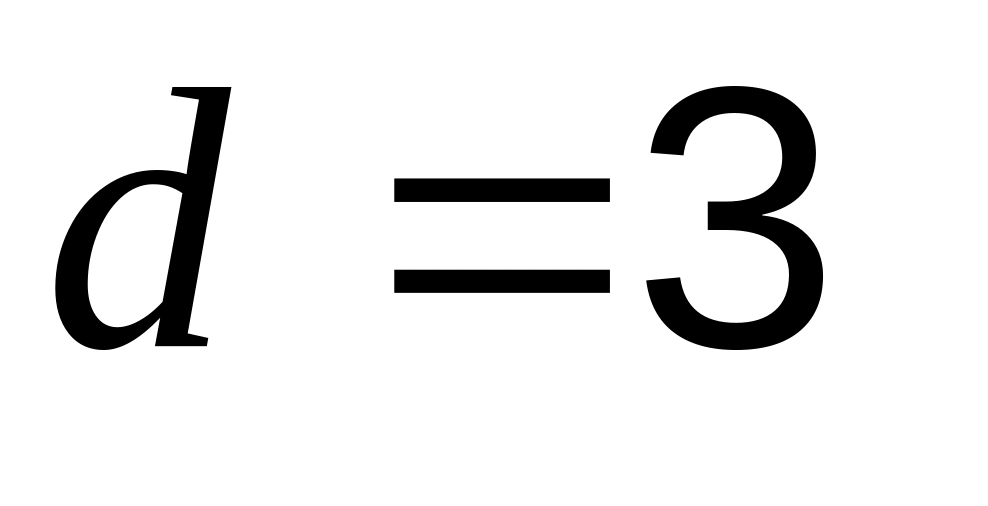см. Определите энергию электрического поля, заключенного в слое диэлектрика.

20. Пять параллельно соединенных одинаковых конденсаторов по 0,1 мкФ каждый заряжается до общей разности потенциалов кВ. Определить среднюю мощность разряда, если батарея разряжается за с. Остаточное напряжение равно 5 кВ.

21. Две концентрические сферические поверхности, находящиеся в вакууме, заряжены одинаковым количеством электричества Кл. Радиусы этих поверхностей см и см. Найти энергию электрического поля, заключенную между этими сферами.

22. Конденсатор емкостью заряжается от источника постоянной эдс через сопротивление . С каким кпд происходит процесс зарядки?

23. Принимая протон и электрон, из которых состоит атом водорода, за точечные заряды, находящиеся на расстоянии см, найдите плотность энергии электрического поля на середине расстояния между ними.

24. На проводящем шаре диаметром d = 0,6 см находится заряд Q = Кл. Шар погрузили в керосин. Определите плотность энергии электрического поля в точках, отстоящих от центра шара на расстояниях 2 и 4 см (при решении задачи считать, что шар расположен на значительном расстоянии от стенок сосуда).

25. П ластину из эбонита толщиной d = 2 мм и площадью поместили в однородное электрическое поле напряженностью 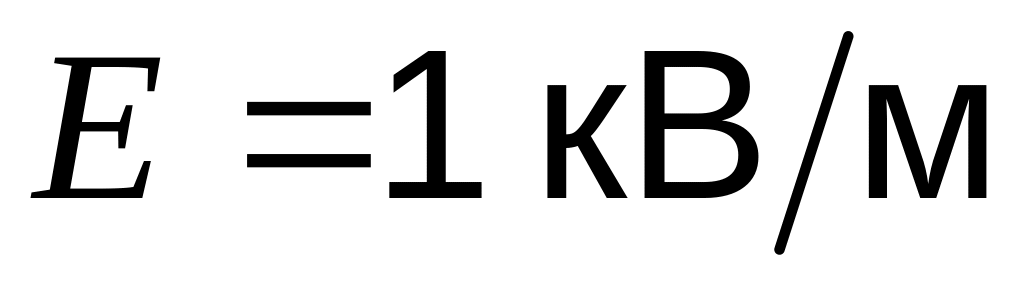, расположив так, что силовые линии перпендикулярны ее плоской поверхности. Найти энергию электрического поля, сосредоточенную в пластине.

6 .26. На систему конденсаторов (рис. 6.4) подано напряжение В. Заряд, сообщен-ный системе, оказался равным Кл. Емкости конденсаторов мкФ, мкФ. Определите емкость конденсатора и энергию каждого конденсатора.

27. Два конденсатора емкостью и и два источника с ЭДС 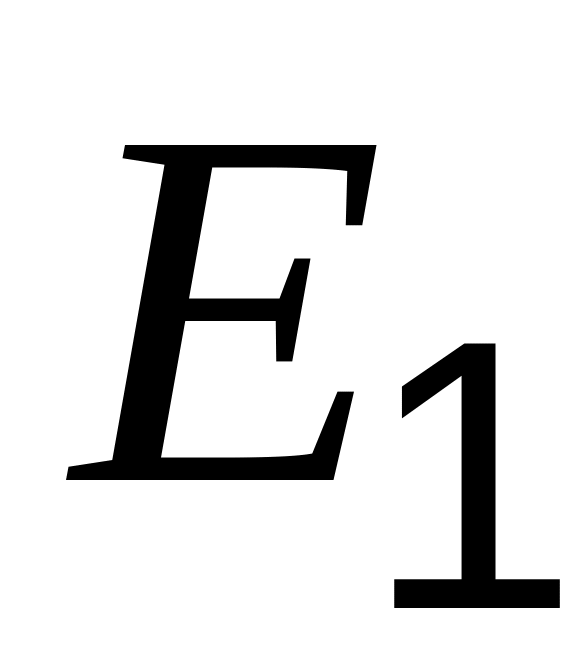и соединяют так, как показано на рис. 6.5. Сначала замыкают ключ , затем его размыкают и замыкают ключ . Как изменится энергия заряженных конденсаторов после размыкания ключа и замыкания ключа ?

6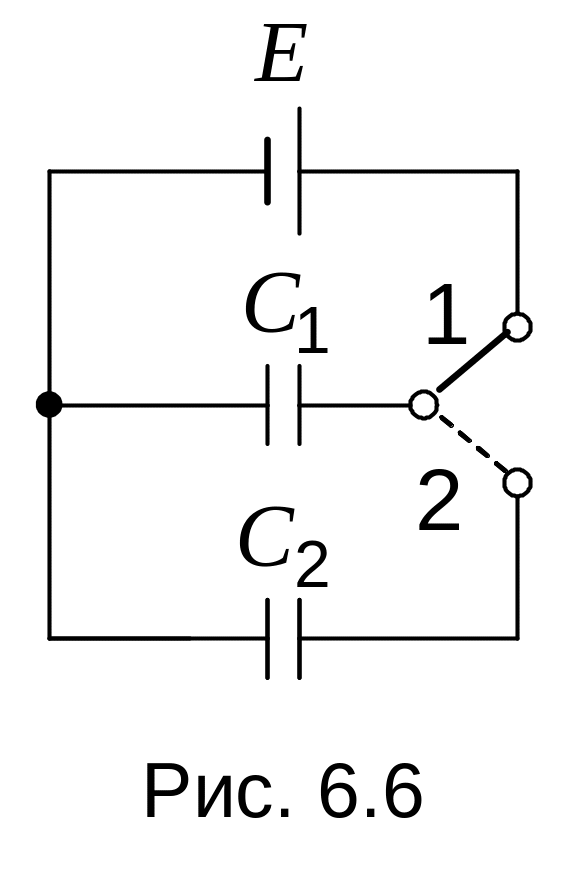 .28. Конденсаторы и подключаются к источнику эдс (рис.6.6). Вначале переключатель находится в положении , так что заряжается конденсатор , затем переключатель занимает положение . Как изменится энергия системы конденсаторов? Рассмотрите случаи: , , .

29. Плоский конденсатор расположен горизонтально так, что одна его пластина находится над поверхностью, другая – под поверхностью жидкости (рис. 6.7). Диэлектрическая проницаемость жидкости , ее плотность . На какую высоту поднимется уровень жидкости в конденсаторе после сообщения его пластинам заряда с поверхностной плотн остью ?

6. Плоский конденсатор при горизонтальном расположении его пластин наполовину погружен в жидкий диэлектрик (рис. 6.8, а). Какую часть пластин конденсатора следует погрузить в тот же диэлектрик при вертикальном положении пластин (рис. 6.8, б), чтобы в обоих случаях емкость конденсатора была одной и той же?

а б

Рис. 6.8

ПриложениЕ 1