5. Электроёмкость. Конденсаторы

Основные формулы

♦ Электроёмкость проводника равна отношению заряда , сообщено проводнику, к потенциалу , который при этом проводник приобрёл:

. (5.1)

♦ Ёмкость уединённого шара радиусом

, (5.2)

где – относительная диэлектрическая проницаемость среды, окружающей шар, – электрическая постоянная.

♦ Электроёмкость (ёмкость) конденсатора

, (5.3)

где – разность потенциалов (напряжение) между пластинами.

♦ Ёмкость плоского конденсатора

, (5.4)

где – площадь пластины конденсатора, – расстояние между его обкладками, – относительная диэлектрическая проницаемость среды, заполняющей конденсатор.

♦ Ёмкость цилиндрического конденсатора

, (5.5)

где – длина цилиндрического конденсатора, и – радиусы цилиндров.

♦ Ёмкость сферического конденсатора

, (5.6)

где , – радиусы сферических обкладок.

♦ Ёмкость батарей из конденсаторов, соединённых параллельно

. (5.7)

♦ Ёмкость батареи из конденсаторов, соединённых последовательно, определяется соотношением

. (5.8)

Методические указания

Электроёмкость уединенного проводника или конденсатора определяет характер электрического поля, возникающего вне и на поверхности проводника (потенциал или разность потенциалов ) при сообщении ему электрического заряда . Поэтому нахождение электроёмкостей связано с расчётом потенциала (разности потенциалов) электрического поля.

Ёмкость проводника (конденсатора) зависит от его размеров, формы, окружающей среды. По формуле (5.2) можно определить ёмкость уединённого шарового проводника. Если проводник имеет иную форму (куб, цилиндр и др.), то для расчёта электроёмкости можно воспользоваться формулами , , где – энергия заряженного проводника, если величины, входящие в эти формулы известны или их можно определить в процессе решения.

Если проводники с одинаковой ёмкостью имели разноимённые заряды, то при их соприкосновении или соединении их с проводником, ёмкостью которого можно пренебречь, равные по модулю заряды нейтрализуются, а оставшийся заряд разделится между проводниками поровну. При соединении шаров в таком случае должны быть равны их радиусы. Если радиусы шаров различны, то заряды уже не будут делиться поровну, поэтому в таких задачах следует воспользоваться законом сохранения электрических зарядов и тем фактом, что после соединения проводников их потенциалы оказываются одинаковыми.

Ёмкость плоского конденсатора определяется по формуле , где – площадь обкладки конденсатора. Если обкладки конденсатора не одинаковы, то под в этой формуле подразумевается только перекрываемая часть площади обкладок.

В тех случаях, когда вносят в конденсатор или выносят из него диэлектрик, а также если меняется расстояние между обкладками конденсатора, но при этом конденсатор не отключают от источника зарядов, то напряжение на обкладках конденсатора меняться не будет (оно будет равно напряжению на плюсах источника), а изменяется ёмкость и заряд на обкладках.

Заряд на обкладках не изменяется, если конденсатор заряжают, а затем отключают от источника зарядов и меняют диэлектрик или расстояние между пластинами конденсатора. При этом меняется ёмкость и напряжение на конденсаторе.

Если между обкладками конденсатора помещают несколько слоёв диэлектриков с относительными диэлектрическими проницаемостями , то такой конденсатор аналогичен последовательному или параллельному соединению нескольких конденсаторов (рис. 5.1).

а) общая ёмкость батареи определяется соотношением => ,

где .

б) общая ёмкость батареи

, где .

а б

Рис. 5.1

Общий метод определения сил, действующих на заряженные тела в электрическом поле (пондеромоторных сил), находящихся как в вакууме, так и в диэлектриках, основан на законе сохранения энергии.

Примеры решения задач

Задача 1. Найти ёмкость системы конденсаторов, изображённых на рис. 5.2, а, б, в.

а б в

г д

Рис. 5.2

Решение.

а) конденсаторы и соединены параллельно, их общая ёмкость .

Теперь параллельный участок можно заменить одним конденсатором ёмкостью , тогда получим эквивалентную схему (рис. 5.2, г), на которой конденсаторы и соединены последовательно, поэтому их общая ёмкость, равная ёмкости батареи из трёх конденсаторов, равна

;

б) конденсаторы , и соединены параллельно, поэтому их общая ёмкость равна , заменив параллельный участок одним конденсатором ёмкостью , получаем эквивалентную схему (рис. 5.2, д).

Общая ёмкость всей системы будет:

;

в) в данной схеме сразу нельзя сказать, какое здесь соединение конденсаторов, последовательное или параллельное. Представим данную схему иначе.

а б

в

Рис. 5.3

Из рис. 5.3, а видно, что левые обкладки конденсаторов на участках и соединены в точке , значит, они имеют одинаковый потенциал . Правая обкладка конденсатора на участке соединена с правой обкладкой на участке , а правая обкладка конденсатора на участке соединена с левой обкладкой конденсатора на участке , значит, этот конденсатор ёмкостью служит перемычкой между конденсаторами ёмкостью на участках и . Поэтому соединим точки и (а также и ) в одну точку. Конденсаторы на участках и оказываются расположенными симметрично относительно конденсатора слева от него. Рассуждая аналогично, расположим конденсаторы на участках и симметрично относительно конденсатора справа от него. Мы получим эквивалентную схему, изображённую на рис. 5.3, б.

Из этой схемы видно, что левые обкладки верхнего и нижнего конденсаторов, расположенных слева от конденсатора , имеют одинаковый потенциал , такой же, как и потенциал точки . Ёмкости этих конденсаторов одинаковы, поэтому заряд этих обкладок одинаков, это означает, что и правые обкладки этих конденсаторов имеют одинаковый потенциал . Тогда согласно схеме на рис. 5.3, б верхняя и нижняя обкладки конденсатора имеют одинаковый потенциал . Следовательно, разность потенциалов между обкладками этого конденсатора всегда будет равна нулю при подключении этой батареи к любому источнику зарядов, заряд на его обкладках тоже всегда будет равен нулю (согласно формуле ), значит, конденсатор всегда будет оставаться незаряженным и его можно убрать из схемы. Схему на рис. 5.3, б заменяем схемой, изображённой на рис. 5.3, в.

Последняя схема рис. 5.3, в содержит две параллельные ветви, содержащие по два одинаковых конденсатора каждая, причём эти конденсаторы соединены последовательно. Ёмкость двух одинаковых последовательно соединенных конденсаторов будет:

.

Общая ёмкость всей системы конденсаторов, равная ёмкости двух параллельно соединённых конденсаторов ёмкостью :

.

Задача 2. Во сколько раз изменится ёмкость плоского конденсатора, если в него внести две тонкие металлические пластины (рис. 5.4, а)? Если соединить их между собой проводом (рис. 5.4, б)?

а б

Рис. 5.4

Решение.

а) при введении двух металлических пластин между обкладками конденсатора образуется система, которую можно рассматривать как батарею из трёх последовательно соединённых конденсаторов одинаковой ёмкости . Ёмкость всей батареи определяется из соотношения: , т.е. , откуда .

Первоначальная ёмкость конденсатора (до введения пластин) была:

, т. е. , следовательно, электроёмкость конденсатора не изменится.

б) соединяя проводом введённые пластины (рис. 5.4, б), мы «закорачиваем» обкладки одного из трёх конденсаторов. Следовательно, в этом случае батарея состоит из двух конденсаторов электроёмкостью каждый. Электроёмкость батареи будет , , т. е. увеличится в 1,5 раза.

Задача 3. Расстояние между обкладками плоского воздушного конденсатора равно мм, радиус круглых обкладок см, напряжение на обкладках конденсатора В. Определить изменение заряда на обкладках, если разность потенциалов между пластинами конденсатора увеличить на 200 В, а расстояние между ними увеличить на 25 %.

Решение.

Электроёмкость плоского конденсатора в начальный момент времени определяем по формуле , где – площадь пластины конденсатора, , тогда .

После изменения расстояния между обкладками электроёмкость конденсатора станет ,

где .

Заряд на обкладках конденсатора в начальный момент времени был:

,

после изменения напряжения заряд будет ,

, где .

Изменение заряда на обкладках

Переведём все физические величины в систему СИ:

, , .

Произведём вычисления:

Кл.

Задача 4. Пространство между обкладками плоского конденсатора частично заполнено диэлектриком с диэлектрической проницаемостью . Площадь пластин конденсатора равна . Определите ёмкость конденсатора в каждом из случаев, показанных на рис. 5.5, а, б, в.

а б в

Рис. 5.5

При заполнении конденсатора диэлектриком с диэлектрической проницаемостью образуется система двух параллельно соединённых конденсаторов с равной площадью обкладок и расстоянием между ними . Один из конденсаторов – воздушный, его электроёмкость , второй конденсатор заполнен диэлектриком, поэтому его электроёмкость . Ёмкость батареи параллельно соединённых конденсаторов определяется как сумма электроёмкостей:

.

Если конденсатор заполнить диэлектриком как показано на 5.5, б, то получается батарея двух последовательно соединённых конденсаторов с площадью обкладок и расстоянием между ними . Один из конденсаторов – воздушный, электроёмкость которого , второй конденсатор имеет электроёмкость .

Общая ёмкость батареи последовательно соединённых конденсаторов определяется из соотношения

=> .

Следовательно, .

На рис 5.5, в, представлена система трёх конденсаторов, два из которых соединены последовательно, а ещё один подсоединён к ним параллельно. Последовательно соединённые конденсаторы имеют одинаковую площадь обкладок , расстояние между обкладками . Один из конденсаторов – воздушный, другой – заполнен диэлектриком. Электроёмкости конденсаторов соответственно равны: ; . Общая электроёмкость: .

.

Третий конденсатор имеет площадь обкладок , расстояние между ними , конденсатор воздушный. Электроёмкость такого конденсатора .

Общая ёмкость системы параллельно соединенных конденсаторов:

.

Задача 5. Два одинаковых плоских конденсатора соединены параллельно и заряжены до напряжения В. После отключения от источника тока расстояние между пластинами одного из конденсаторов уменьшили в два раза. Каким станет напряжение на конденсаторах.

Решение.

При параллельном соединении конденсаторов и общая емкость будет:

.

Заряд батареи .

При уменьшении в два раза расстояния между пластинами конденсатора его электроёмкость увеличится в два раза (согласно формуле ) и станет , тогда их общая электроёмкость .

Заряд станет .

По закону сохранения электрического заряда , так как батарея конденсаторов отключена от источника. Следовательно, , откуда .

.

Задача 6. Два одинаковых плоских воздушных конденсатора соединены последовательно, и к ним подведено постоянное напряжение . Первый конденсатор заполняют диэлектриком с диэлектрической проницаемостью . Во сколько раз изменится напряжённость электрического поля в каждом из конденсаторов?

Решение.

Обозначим ёмкость каждого конденсатора до соединения в батарею . При последовательном соединении напряжение . Так как конденсаторы одинаковые, то .

При заполнении первого конденсатора диэлектриком с диэлектрической проницаемостью его электроёмкость станет . Общая ёмкость батареи

.

Заряд при последовательном соединении одинаков на каждом конденсаторе и .

Напряжение на конденсаторе, заполненном диэлектриком, равно: , , следовательно, напряжение уменьшается в . Так как напряжённость поля и напряжение связаны соотношением: , то при уменьшении напряжения в раз во столько же раз уменьшается и напряжённость электрического поля в первом конденсаторе.

Напряжение на конденсаторе, не заполненном диэлектриком, станет

.

,

значит, напряжение увеличится в раз по сравнению с первоначальным. Во столько же раз увеличивается напряжённость электрического поля во втором конденсаторе.

Задача 7. Два параллельных цилиндрических провода радиусом  мм расположены так, что расстояние между их осями  см. Найдите ёмкость единицы длины такой системы (система находится в воздухе).

Решение.

Заряды можно считать равномерно распределёнными по поверхности проводников, так как . Ёмкость каждой единицы длины системы будет определяться по формуле

,

где – заряд, приходящийся на единицу длины каждого провода; – разность потенциалов между проводами.

Напряжённость поля в точке , находящейся на расстоянии от положительно заряженного провода: или

.

Разность потенциалов между проводами

Тогда ёмкость каждой единицы длины

.

Выразим все величины в системе СИ:

; .

Вычисления дают следующий результат:

.

Задача 8. Конденсатор ёмкостью подключён к батарее с эдс . Вплотную с одной из обкладок конденсатора расположена тонкая металлическая пластинка. Какими станут заряды на обкладках конденсатора, если пластинку сдвинуть параллельно обкладкам в середину конденсатора, не снимая с неё заряда?

Решение.

Металлическая пластинка, присоединённая к пластине конденсатора, приобретает заряд , который не изменится при перенесении пластинки в центр между обкладками конденсатора. Помещая металлическую пластину в середине конденсатора, мы делим его на два конденсатора ёмкостью ; ёмкость , тогда ,

где – расстояние между обкладками конденсатора (пластинами 2 и 3 на рис. 5.7).

П ластина 1 одновременно является положительной обкладкой для левого конденсатора и отрицательной – для правого. На ней вследствие явления индукции наводятся заряды и .

Конденсаторы и соединены последовательно (чисто формально), поэтому , где ; , тогда , , – модули зарядов пластин 3 и 2.

По закону сохранения электрического заряда: или .

Р ешаем систему уравнений:

,

, тогда

.

З адача 9. Зазор между обкладками плоского конденсатора заполнен изотропным диэлектриком, проницаемость которого изменяется в перпендикулярном обкладкам направлении по линейному закону от до . Площадь каждой обкладки , расстояние между ними . Определить емкость конденсатора.

Решение.

Н

Рис. 5.8

аправим ось вверх, начало координат совместим с нижней пластиной. По условию задачи диэлектрическая проницаемость меняется по линейному закону, т. е.

, (1)

где и – некоторые постоянные величины, которые можно найти из граничных условий: при , отсюда , при , следовательно, . Тогда зависимость принимает вид

. (2)

При сообщении нижней пластине заряда образуется электрическое поле напряженностью ,

где – поверхностная плотность зарядов, , тогда

(3)

Напряженность поля и потенциал связаны соотношением: , поэтому (4)

проинтегрируем выражение (4), получаем:

.

Емкость конденсатора , т. е.

З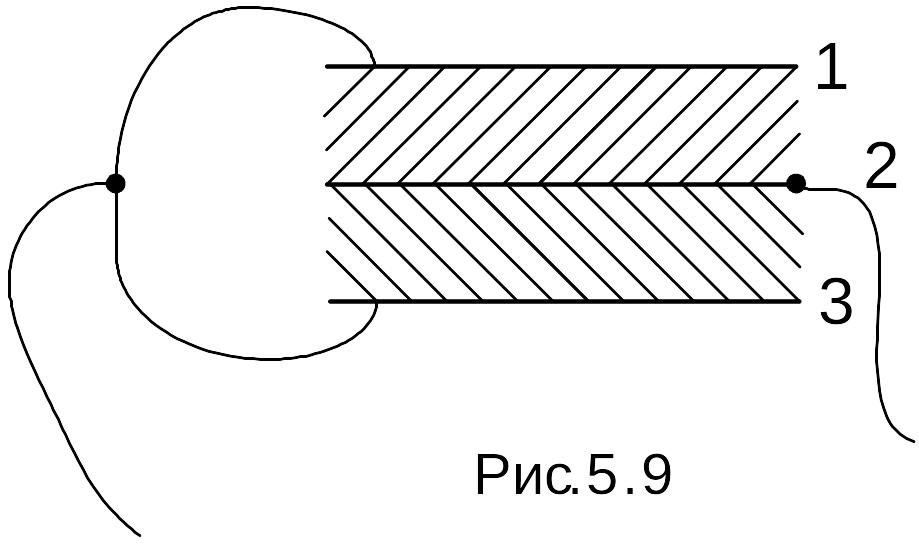 адачи для самостоятельного решения

1. Конденсатор состоит из трех полосок фольги площадью каждая, разделенных слоями слюды толщиной мм. Крайние полоски фольги соединены между собой (рис. 5.9). Какова емкость такого конденсатора?

5. О пределите заряды на каждом из конденсаторов в цепи, изображенной на рис. 5.10, если мкФ, мкФ, мкФ, В.

5. Пять конденсаторов одинаковой емкости соединены последовательно в батарею. Параллельно одному из конденсаторов подключен статический вольтметр, емкость которого в два раза меньше емкости каждого конденсатора. Вольтметр показывает 500 В. Какова разность потенциалов на всей батарее?

5. Два проводящих шара диаметром мм и м, каждый соединяются проводником. До соединения на шарах находились заряды и . Каким будет потенциал шаров после их соединения?

5.5. Шар радиусом см заряжен до потенциала В, а шар радиусом см до потенциала В. Определить потенциал шаров после того, как их соединили металлическим проводником. Емкостью соединительного проводника пренебречь.

5.6. На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью . Расстояние между пластинами мм. На сколько изменится разность потенциалов на его обкладках при увеличении расстояния между пластинами до 3 мм?

5.7. В плоский конденсатор вдвинули плитку парафина толщиной 1 см, которая вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость?

5.8. Электроемкость плоского конденсатора равна 1,5 мкФ. Расстояние между пластинами равно 5 мм. Какова будет электроемкость плоского конденсатора, если на нижнюю пластину положить лист эбонита толщиной 3 мм.

5.9. Между пластинами плоского конденсатора находится плотно прилегающая стеклянная пластинка. Конденсатор заряжен до разности потенциалов 100 В. Какова будет разность потенциалов, если вытащить стеклянную пластинку из конденсатора?

5.10. Шарик радиусом 2 см заряжается отрицательно до потенциала 2 кВ. Найти массу всех электронов, составляющих заряд, сообщенный шарику.

11. шаровых капель радиусом заряжены до одинакового потенциала . Все капли сливаются в одну большую. Определите потенциал, и плотность заряда на поверхности большой капли.

12.  Шарик, заряженный до потенциала 792 В, имеет поверхностную плотность заряда . Найти радиус шарика.

13. Площадь пластин плоского воздушного конденсатора равна 0,01 м², расстояние между ними 5 мм. К пластинам приложена разность потенциалов 300 В. После отключения конденсатора от источника напряжения пространство между пластинами заполняется эбонитом. Какова будет разность потенциалов между пластинами после заполнения? Найти емкость конденсатора и поверхностные плотности заряда на пластинах до и после заполнения.

5.14. Обкладками сферического конденсатора являются две проводящие сферы радиусами см и см. Внешняя сфера радиусом заземлена, на внутренней сфере помещен заряд Кл. Определите электроемкость данного сферического конденсатора и потенциал первой сферы. Пространство между сферами заполнено парафином .

5.15. Определите емкость плоского конденсатора, между обкладками которого находится стекло мм, покрытое с обеих сторон слоем парафина толщиной мкм. Площадь обкладок конденсатора .

5.16. Найти емкость конденсатора, образованного двумя одинаковыми шариками радиуса , находящимися в среде с диэлектрической проницаемостью . Расстояние между центрами шариков равно . Заряды полагать распределенными с постоянной плотностью по поверхности шариков. Вычислить при условии, что мм, мм, .

5.17. Коаксиальный электрический кабель состоит из центральной жилы и концентрической цилиндрической оболочки, между которыми находится диэлектрик . Найти емкость единицы длины такого кабеля, если радиус жилы равен 1,3 см, радиус оболочки 3 см.

5.18. Цилиндрический конденсатор состоит из внутреннего цилиндра радиусом 3 мм, двух слоев диэлектрика и внешнего цилиндра радиусом 1 см. Первый слой диэлектрика толщиной 3 мм примыкает к внутреннему цилиндру. Найти отношение падений потенциала в этих слоях.

5.19. Во сколько раз изменится емкость плоского воздушного конденсатора, если уменьшить площадь его обкладок в 1,5 раза, уменьшить расстояние между ними в 2 раза и пространство между обкладками заполнить слюдой с диэлектрической проницаемостью ?

5 .20. Плоский воздушный конденсатор с площадью обкладок и расстоянием между ними подключим к источнику постоянного напряжения . Найти изменение заряда на обкладках конденсатора, если в пространство между ними ввести пластинку с диэлектрической проницаемостью , не отключая от источника. Толщина пластинки (рис. 5. 11).

5.21. Воздушный конденсатор с зарядом на обкладках , площадью обкладок и расстоянием между ними погружают в жидкость с диэлектрической проницаемостью на его объема. Найти напряжение на обкладках конденсатора после погружения.

5.22. Конденсатор электроемкостью был заряжен до разности потенциалов В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов  В, напряжение на нем изменилось до 400 В. Вычислить емкость второго конденсатора.

5.23. Конденсатор электроемкостью был заряжен до разности потенциалов В и соединен со вторым конденсатором электроемкостью мкФ, заряженным до разности потенциалов  В. Найти заряд , перетекший с пластин первого конденсатора на второй.

5.24. Три одинаковых плоских конденсатора соединены последовательно. Электроемкость такой батареи конденсаторов равна 89 мкФ. Площадь каждой пластины равна 100 см². Диэлектрик – стекло. Какова толщина стекла?

5.25. На два последовательно соединенных конденсатора и нкФ подано постоянное напряжение В. Определить напряжения и на конденсаторах и заряд на их обкладках. Какова емкость системы?

5.26. Определить емкость батареи конденсаторов, изображенной на рис. 5.12. Емкости и известны.

5.27. На рис. 5.13 изображена батарея конденсаторов, подключенная к источнику напряжением В. Определить общий заряд батареи , если нФ, нФ, нФ.

5.28. Дана схема (рис. 5.14). Емкость нФ. Напряжение  В. Найти заряды , , и на конденсаторах.

Рис. 5.12 Рис. 5.13 Рис. 5.14

5.29. В некоторой цепи имеется участок, изображенный на рис. 5.15.

Потенциалы точек , , равны соответственно , , , а емкости конденсаторов , и . Найти потенциал точки .

5.30. Как изменится заряд на конденсаторах и в схеме, показанной на рис. 5.16, при включении между точками и конденсатора емкостью ?

; .